灰色线性回归组合模型在北京地面沉降分层预测中的应用

周 毅，罗 郧，贾三满，田 芳

（1．北京大学地球与空间科学学院，北京 100871；2．北京市水文地质工程地质大队，北京 100195；3．中国地质环境监测院，北京 100081）

1982年，中国学者邓聚龙教授创立了灰色系统理论，这是一门新兴的横断学科，是研究少数据、贫信息不确定性问题的新方法[1]。经过刘思峰、林益等学者的努力使灰色系统理论不断完善和发展，同时基于该理论形成了GM(1,1)模型，GM(0，N)模型、verhulst模型等灰色预测模型并被广泛应用于自然科学、社会科学、工程技术等各个领域。

地面沉降是一个复杂地、系统地过程。诱发地面沉降的因素有很多，有土体天然固结、有地下水过度开采、有工程建设荷载等等。总之，这是一个包含土层—地质作用—人类活动的复杂系统[2]。那么复杂系统就涉及到许多的未知因素，包括相互关系未知，结果为未知等，因此利用灰色系统理论将其概化为一个单纯的数学模型来进行预测就很有意义。例如，郭小萌[3]进行了基于矩阵的GM(1,1)模型对北京市平原区进行了地面沉降预测，取得了较好的效果。宫相霖[2]利用灰色系统建立了地面沉降与地下水位变化的映射GM(1,2)模型对上海的地面沉降发展态势进行了预测。

本文以北京地面沉降监测站分层监测的数据为支撑。在地面沉降快速发展阶段中，各种因素对地面沉降的影响无法定量表述的情况下，利用GM(1,1)模型与线性回归模型相组合对地面沉降进行模拟和预测，既能体现阶段地面沉降的快速发展趋势，又弥补了单一GM(1,1)模型无法能描述变量间的线性关系的缺点。

1 灰色线性回归组合模型

灰色线性回归组合模型可以看作是普通均值GM(1,1)模型与线性相组合。针对原始数据按以下步骤建立模型：

（1）设原始数据序列 X(0)有n个监测值分别为：

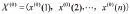
（2）对 X(0)的一阶累加（1-AGO）序列 X(1)为：其中

由此可得 X(1)的预测值为：

其中，C1=0时，上式为一元线性回归模型；当C2=0时，上式为GM(1,1)模型；当C1≠0，C2≠0上式既包含指数增长趋势，又包含线性项的灰色线性回归模型。对上式进行一次累减还原即可得到原序列的预测值(0)X 。（6）预测精度检验

2 研究实例

2.1 研究区概况

北京地面沉降最早于上世纪30年代中期发生在西单—东单一带，先后经历形成阶段（1955～1973）、发展阶段（1974～1983）、扩展阶段（1984～1998）和快速发展阶段（1999年至今）。随着北京不断增加的水资源供给需求，地下水过量超采形势依旧，地面沉降仍呈现快速发展趋势。截止2012年北京地面沉降区分布呈南北两个大区：北区主要包括昌平沙河－八仙庄沉降区、朝阳来广营沉降区和东八里庄－大郊亭沉降区。区内最大累计沉降量为1414mm，位于昌平沙河－八仙庄沉降区内的八仙庄地区；南部沉降区主要为大兴榆垡－礼贤沉降区，该沉降区与河北相邻地区连接。区内最大累计沉降量位于礼贤沉降区达1137mm[4]。

为实时监测地面沉降发展趋势，研究地面沉降成因机理，最终实现预警预报系统。北京市先后于2004年和2008年建设完成了顺义天竺等7个地面沉降监测站。监测站内采用基岩标—分层标静力水准测量系统对各监测站所处的地层进行分层监测。本文选用北京东部典型沉降区内某地面沉降监测站内分层监测数据作为原始数据的来源。具体分层监测情况见表1。

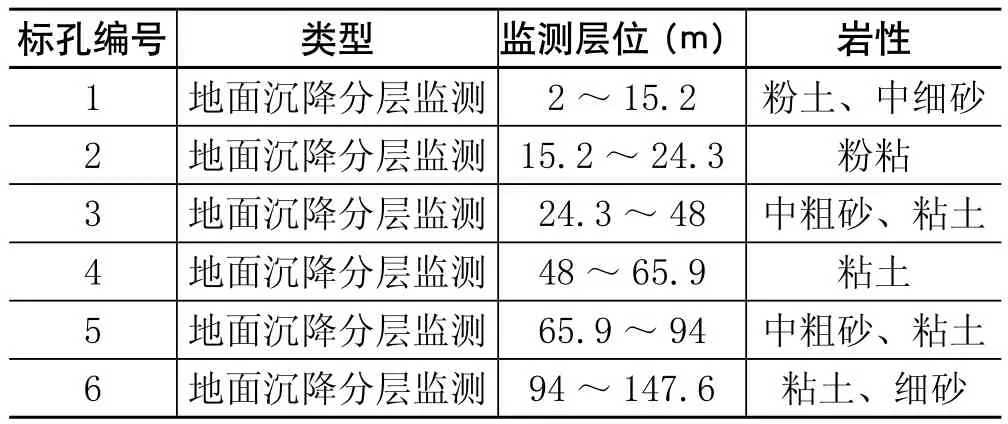
表1 地面沉降分层监测概况

2.2 建立组合模型A-F

选取该站2004～2012年监测的部分标孔累计沉降量监测数据作为的原始数据序列(表2)，以分层监测标孔为单元建立一阶累加（1-AGO）地面沉降模型组。例如：1层监测标的1-AGO灰色线性回归组合模型记为模型A，2层监测标的记为模型B，以此类推。具体建模步骤如下：

(1)建立模型A

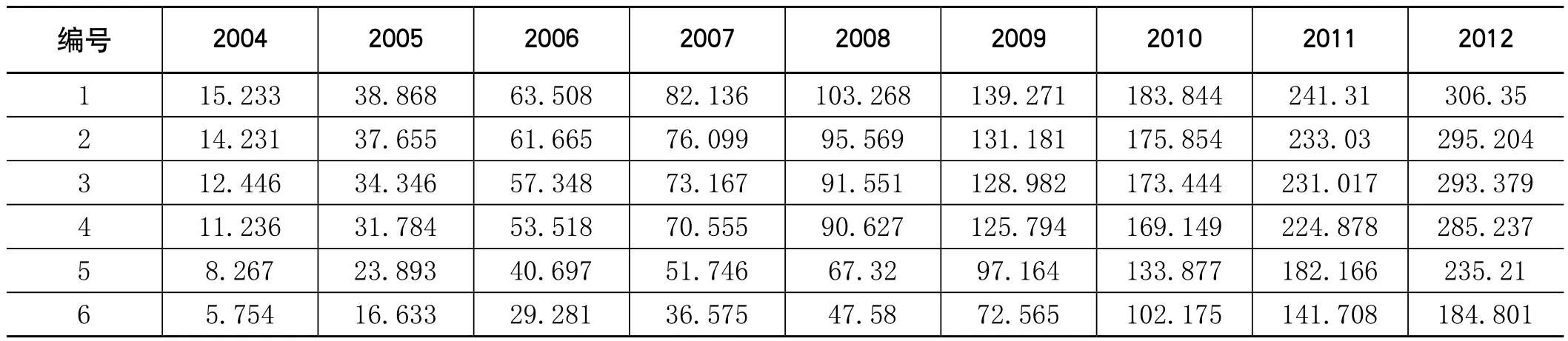
表2 地面沉降分层监测数据（2004～2012年）

2.3 预测结果对比分析

对原始数据序列作1—AGO可得一阶累加数据：

基于灰色线性回归模型的短期预测精度较高的特点，利用模型组A－F模拟2004～2012年的沉降值，并预测2013年的沉降值。因此，将={15.233 54.101 117.609 199.745 303.013 442.284 626.128 867.438 1173.788}令带入模型组A，可得一阶累加沉降值=（18，56.3，113.5，193.7，302.2，445.3，631，868.8，1170.5，1550.6，2027）。对进行一次累减还原，，=(298.6088,-44.5580,-303.7192)

故1-AGO生成序列的灰色线性回归组合模型A为：，则参数v的估计值=0.20414948，

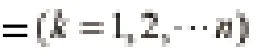
(2)按模型A的建立方式依次建立模型B－F，具体见表3。可得1号标孔2004～2013年的累计沉降量分别为18mm，38.3mm，57.2mm，80.2mm，108.5mm，143.1mm，185.7mm，237.8mm，301.7mm，380.1mm。同理，可得2～6号标孔的2004～2013年的累计沉降量（表5）。计算模型组残差和相对误差，发现2004年部分监测层位沉降量相对误差超出了模型一般精度要求，分析原因可能为监测初始年，各分层标孔还未稳定，因此该数据在数学模型拟合时

表3 1-AGO的灰色线性组合模型

其误差较大。但2005～2013年各标孔预测模型相对误差均符合模型要求，且绝大多数相对误差小于0.1，模型精度达到较高要求。经过后残差检验（表4），各标孔后残差比均小于0.35，小误差概率为1，模型符合建模要求，且精度良好。

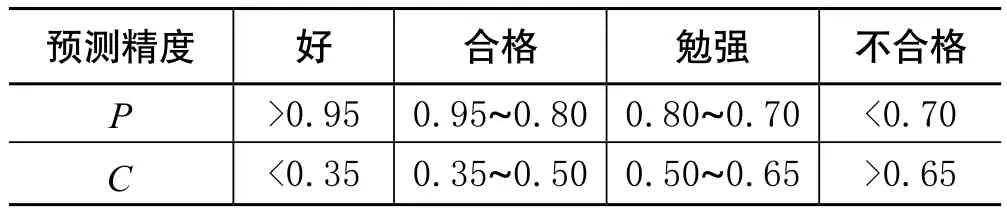
表4 模型精度评定表

利用该模型组模拟2004～2012年的各监测层位累计沉降量，发现其相对误差随着监测层位的不断加深，平均相对误差值不断增加。预测2013年的沉降量发现，地表沉降量（1号标孔）预测结果与实测误差为6.375mm，占实测结果的1.7%，同时，其它监测层位最大累计沉降量相对误差不超过实测值的6.5%。利用实测结果值与预测结果值建立相关性分析，得出其相关系数 ，说明实测结果与预测结果有着显著的相关性。

为进一步对比模型精度，将灰色线性回归组合模型与普通均值GM(1,1)模型进行对比，通过两种模型分别进行沉降模拟，发现2004-2012年基于两种模型的各分层模拟年沉降值平均误差均在3～4mm左右，模型的精度均很高（图1）。但通过拟合的数学模型来预测2013年沉降量时，灰色线性回归组合模型平均误差为10mm，普通均值GM(1,1)模型平均误差达32mm。绘制2013年累计沉降量预测与实测对比曲线图2，可以看出灰色线性回归组合模型预测未来沉降量时其精度要远高于GM(1,1)模型（图2）。

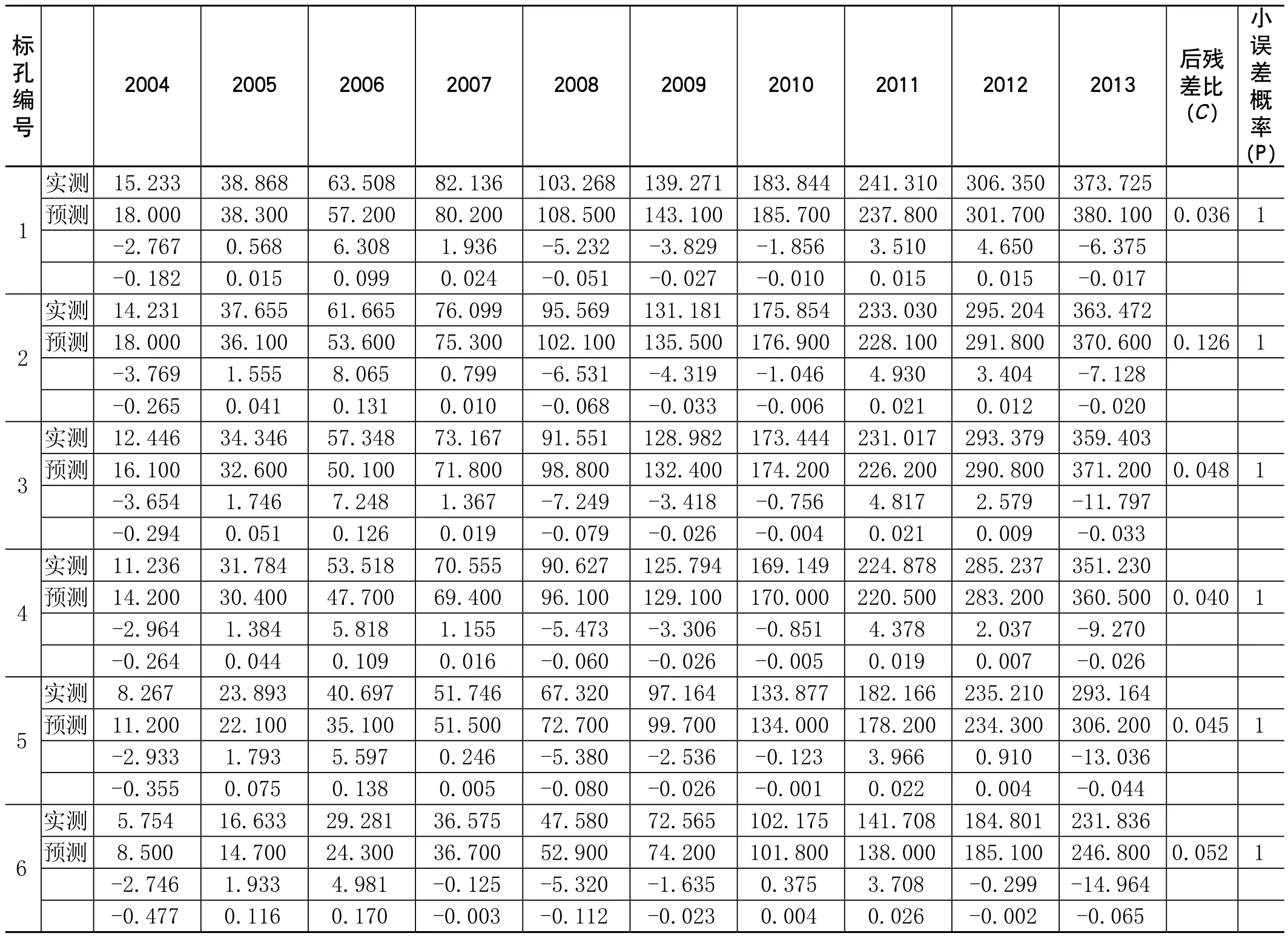
表5 1～6号标孔分层累计沉降量预测结果表（2004～2013年）

3 结论

地面沉降的诱发因素很多，各种不确定因素均对地面沉降的预测产生影响。在缺乏对地区地面沉降与其影响因素定量研究的基础上，采用灰色线性回归组合模型对地面沉降进行预测是切实可行的。本文利用灰色线性回归组合模型对北京东部某典型地面沉降区内地层进行分层沉降模拟，发现利用组合模型进行预测其精度要高于普通均值GM(1,1)模型。同时，由于该方法建立在少样本，贫数据的基础上，因此只需要利用单一的累计沉降量数据，通过发掘其序列监测值内在的关联，建立数学模型，即可模拟预测未来的沉降量。在精度上，地表沉降量（1号标孔）短期预测结果与实测误差为6.375mm，占实测结果的1.7%，精度达到很高的水平，因此，只要不断引入监测数据对模型进行适度校正，即可利用该模型预测未来短期内的沉降量

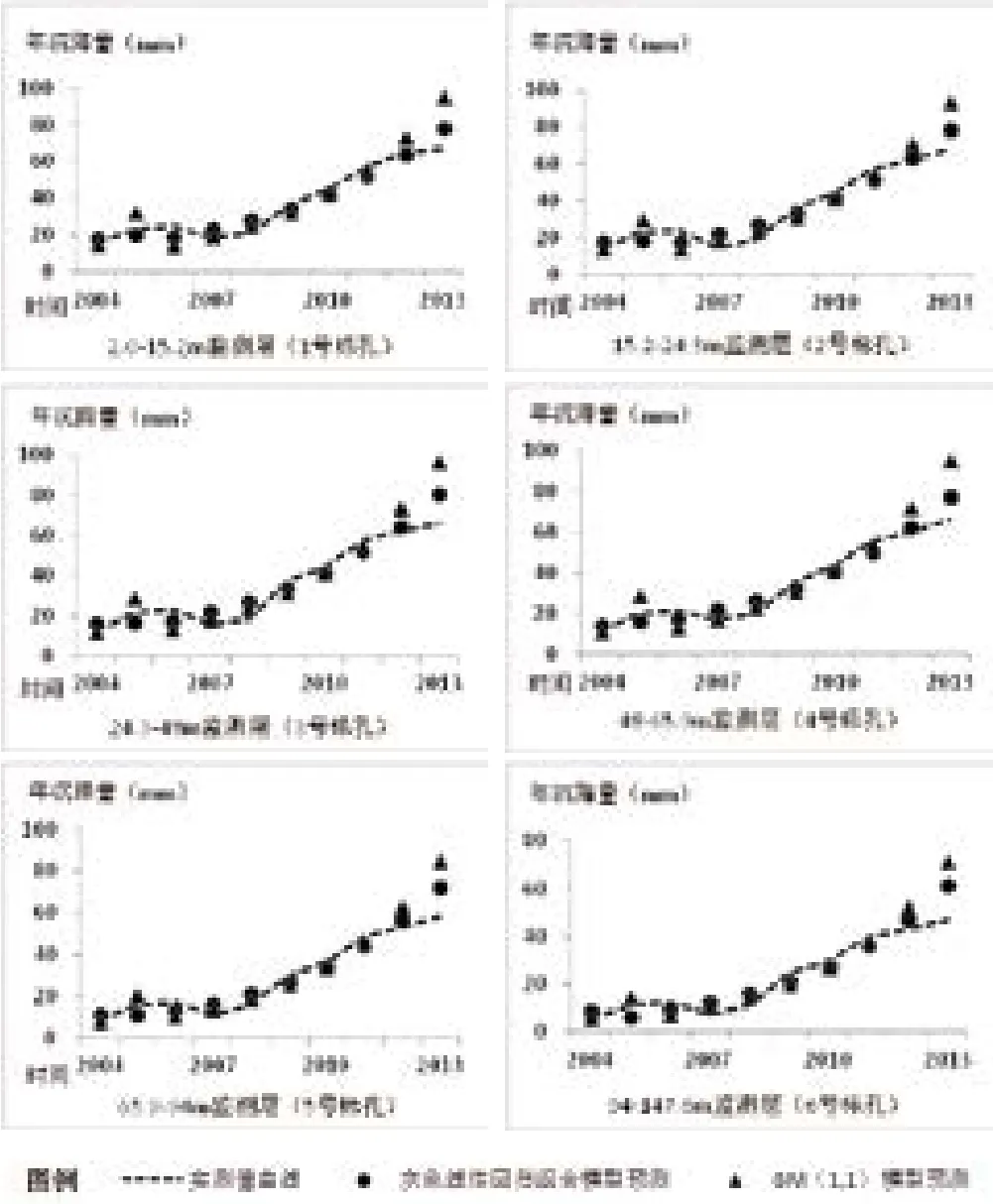
图1 两组模型分层预测结果与实测结果对比

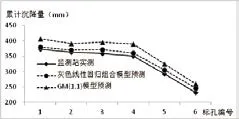
图2 两组模型预测2013年沉降量结果与实测结果对比

[1]刘思峰,谢乃明等.灰色系统理论及其应用[M].北京：科学出版社,2013.

[2]宫相霖,董荣鑫.灰色系统在地面沉降分析中的应用[J].上海地质,2003,3：16～21.

[3]郭小萌,宫辉力,朱 锋等.基于矩阵的GM(1,1)模型预测地。面沉降[J].水文地质工程地质,2013,40(6)：101～105.

[4]罗 勇,周 毅,田 芳等.北京地面沉降监测年度报告(2012年)[R].北京市水文地质工程地质大队,2013.

[5]陈 博,王建国.灰色线性回归组合模型算法研究[J].西安文理学院学报：自然科学版,2012,15(1)：82～85.

[6]马保卿,张 荫.灰色线性回归组合模型在地面沉降预测中的应用[J].铁道勘察,2008,5：20～22.

[7]刘国仕,何亮云,薛建华等.灰色线性回归组合模型在沉降监测中的应用[J].长沙理工大学学报（自然科学版,2012,12：32～36.