永磁同步电机矢量控制系统的建模与仿真

胡杨昊，易灵芝，李真贵

（湘潭大学 信息工程学院，湖南 湘潭 411105）

0 引言

随着高性能永磁材料的发展，永磁同步电机（PMSM）因体积小、效率高、功率因数高、转动惯量小等优点，在各个领域得到了广泛的应用[1]。同时永磁同步伺服系统是一个非线性、强耦合、时变的复杂系统，因此需要通过合理的数学变换，建立其解耦的状态方程。

1971年德国学者Blaschke 等[2,3]提出了矢量控制（VC）理论，使交流电机转矩和磁通的控制实现解耦。目前永磁同步电机伺服系统中多采用空间矢量控制（SVC）技术[4,5]，不仅可以提高逆变器的电压输出能力，且恒定的开关频率适合数字化控制。本文基于矢量控制技术，建立了PMSM 伺服系统的仿真模型，并进行了仿真验证。

1 永磁同步电机的数学模型

为简化分析，作如下假设： ①忽略铁心饱和效应；②气隙磁场呈正弦分布；③不计涡流和磁滞损耗。永磁同步电机在三相静止坐标系U-V-W 下的电压方程为：

在三相绕组中有：

采用Clarke 变换和PARK 变换，将三相固定坐标系转换为两相旋转坐标系，得到解耦后的状态方程为：

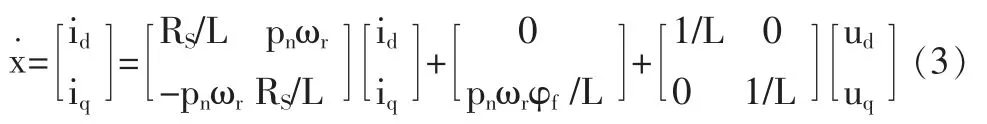
转矩方程为：

运动方程为：

式中，id、iq—dq 轴电流；ud、uq-dq 轴电压；RS—定子电阻；L—等效dq 轴电感；pn—极对数；φf—转子磁势；ωr—转子机械角速度；J—折算到电机轴上的总转动惯量；B—粘滞摩擦系数；TL—折算到到电机轴上的总负载转矩；Te—电磁转矩。

从式（4）可看出系统的电压电流是紧密耦合的。通过矢量控制方式实现交流电机的解耦控制，则式（4）可简化为：

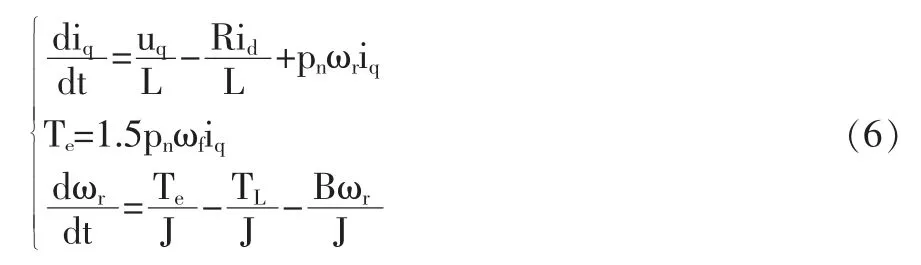
通过以上数学模型可知，永磁同步电机矢量控制原理如图1 所示。

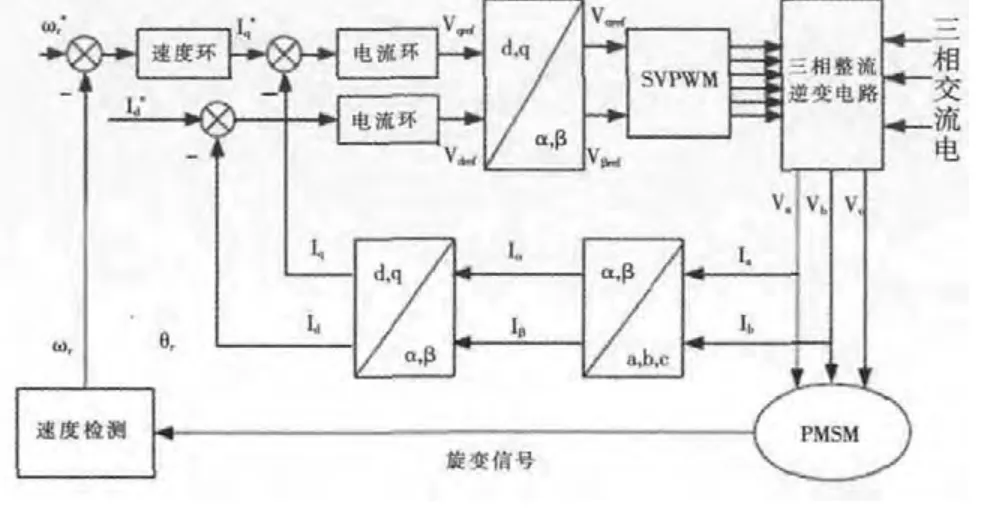
图1 PMSM 伺服系统矢量控制原理

2 控制系统建模

在Matlab7.0 环境下，构建出永磁同步电机伺服系统矢量控制仿真模型如图2 所示。系统由坐标变换、扇区计算、作用时间计算、基本电压矢量作用时间、导通时间计算、PWM 生成等子模块组成。

图2 PMSM 伺服系统矢量控制仿真模型

2.1 坐标变换模块

坐标变换分为： 三相电流转换为两相的clarke 变换，如式（7）所示；两相电流转换为励磁和转矩电流的park 变换，如式（8）所示；磁场和转矩电压转换为两相的park 变换，如式（9）所示：

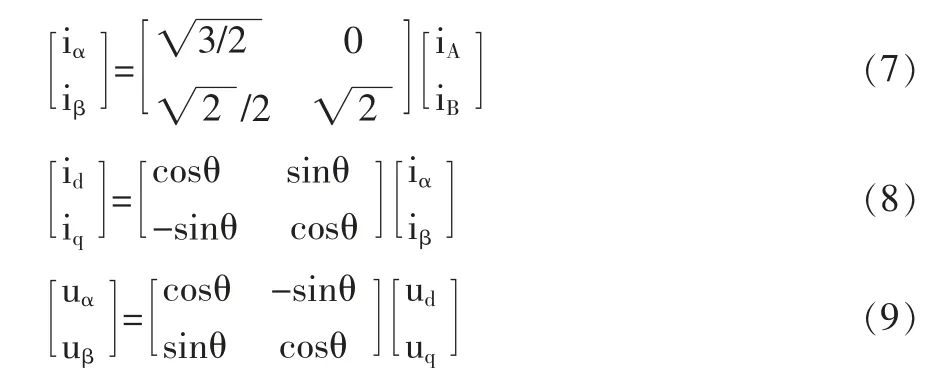
2.2 空间矢量扇区计算模块

各个扇区与uα、uβ的关系如式（10）所示，其中：uα、uβ—等效两相相电压；u1、u2、u3—扇区计算因子；N—扇区数。

2.3 矢量作用时间因子计算模块

两个相邻的电压空间矢量在一个PWM 周期中的作用时间，可以通过式（11）计算出来。其中：uα、uβ—两相相电压；T—开关周期；U—直流母线电压；X、Y、Z—导通时间因子。

2.4 基本电压矢量作用时间模块

为了计算不同扇区的导通时间，扇区和导通时间的对应关系如表1 所示。

表1 扇区和导通时间

当T1+T2＞T 时：

其中： T1、T2—相邻两基本矢量的导通时间；T—开关周期；T1'、T2'—处理后的相邻矢量导通时间。

2.5 导通时间计算模块

计算方程如式（12）所示：

其中： t1、t2—等效的导通时间；t0—0 矢量的导通时间；CMP0、CMP1、CMP2—导通时间因子。

2.6 PWM 生成模块

该模块实现了将三个桥臂导通时间转换为器件的0或1 开关状态，仿真模型如图3 所示。

3 仿真及结果分析

采用上述永磁同步电机伺服系统矢量控制系统仿真模型，对永磁同步电机进行空载变速及恒速加载运行仿真。电机参数为： Pn=50*746W；Vn=460V；np=2；Rs=0.087；Lm=34.7e－3H；J=0.00095kg·m2；B=0；Vdc=350V；Ts=2μs；ψr0=10－3Wb。

图4 是对给定参考转速为±100rad/s 变化的方波信号，电机空载条件下运行时的仿真曲线。仿真曲线包括： 三相电流ia、ib和ic；电机转速和电磁输出转矩。相电流达到稳态，转矩输出保持为零，参考转速信号由+100rad/s跳变为－100rad/s，电磁转矩跳变为负的最大值，电机开始反向加速，直到电机转速达到负的最大值，电机输出转矩再次跳变为零，电机转速保持为－100rad/s。

图3 PWM 生成模块

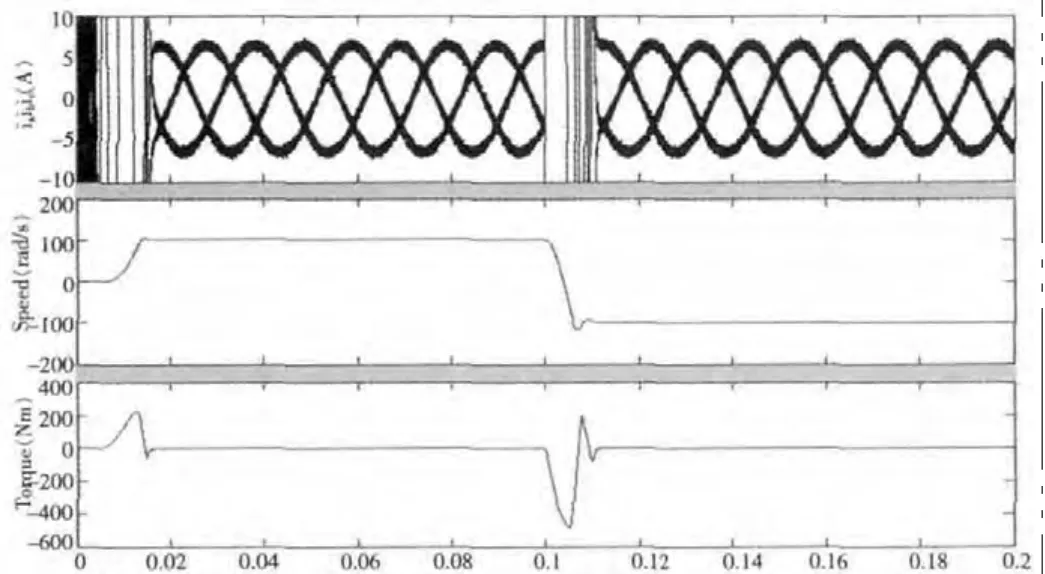
图4 空载时系统仿真曲线

图5 是带负载时的控制仿真曲线，当电机转速达到稳定值+100rad/s 后，在0.1s 时，给电机忽加Tl=100Nm的负载，此时电机输出转矩从零迅速跳变为额定负载值，转速瞬时跌落约为2%，恢复时间约为0.06s，系统具有良好的抗负载扰动的能力。

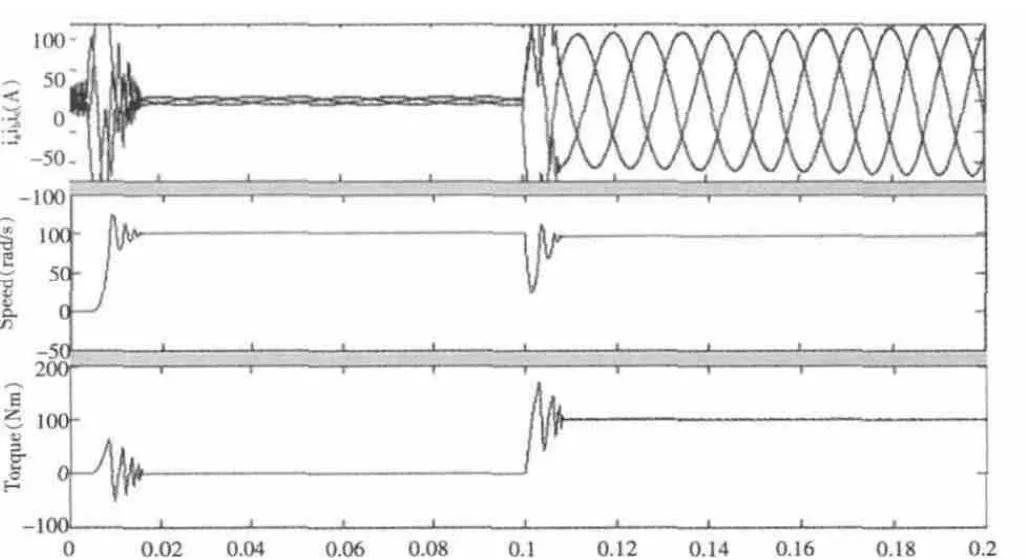
图5 加负载时的系统仿真曲线

4 结束语

本文通过对永磁同步电机数学模型的分析，建立了PMSM 的矢量控制系统，并在Simulink 环境下建立了该系统的仿真模型；进行仿真实验。仿真结果表明，在空载和负载情况下，系统能平稳运行且具有良好的速度响应，为PMSM 伺服系统的控制提供了有效的控制方法。

[1] 陈伯时.电力拖动自动控制系统（第2 版）[M].北京：机械工业出版社，2000.

[2] Liang ZH. Study of Intelligent Conrtol for Permanent Manget Synchornous Motor of AC Servo System[D].Shenyang: Shenyang University of Technology,2009.

[3] Li SY.Fuzzy,Neura and Intelligent Contorl Theory[M].Harbin: Harbin University of Technology PublishingHouse，2006.

[4] 赵西梅.交流电机伺服系统的发展现状及研究热点[J].伺服控制，2010，1.

[5] 张彦照.永磁同步电机伺服系统[D].南京航空航天大学，2009.