基于局部学习的遥感图像融合

高东生（南京航空航天大学，江苏 南京 210016）王 颖（中国科学院自动化所，北京 100086）

基于局部学习的遥感图像融合

高东生（南京航空航天大学，江苏 南京 210016）
王 颖（中国科学院自动化所，北京 100086）

本文提出了一种基于局部学习的遥感图像融合方法。其基本思想是在局部区域对融合图像与全色图像建立对应的局部线性关系。由于图像数据在局部区域相对简单，因此局部模型相比全局模型更为合理。在局部学习的基础上，将全色图像与融合图像的全局回归误差表示为图拉普拉斯的形式，其本质是利用局部学习使得融合图像保持全色图像的流形结构。同时为了保持多光谱图像的性质，通过图像的尺度空间表示，建立融合图像与多光谱图像之间的尺度关系。最后通过集成融合图像的二次拉普拉斯形式和尺度空间表示，构建图像融合的全局目标函数。为了优化目标函数，本文提出了闭合求解法和快速迭代求解法。实验结果表明：本文所提出的融合方法比传统融合方法具有更好的效果。

局部学习；遥感图像融合

1 简介

在遥感图像处理领域，对于光学传感器,图像的空间分辨率和光谱分辨率是一对矛盾的因素。要获得高空间分辨率的图像就只能以单光谱工作，而要获得更多光谱就必须降低空间分辨率。为了同时提高图像的空间分辨率和光谱分辨率，人们提出了利用融合全色图像（高空间分辨率单光谱图像）和多光谱图像（低空间分辨率）来得到高空间分辨率多光谱图像的方法。总结已有的图像融合方法,可以将其分为三类:

第一类是基于颜色空间的转换方法[1,2,3]。这些方法先将多光谱从原颜色空间转换到另外一种颜色空间，这样可以将亮度信息分量和颜色信息分量分开，然后用单光谱的全色图像替换亮度信息分量，由此得到替换后的颜色空间表示，最后再对新的颜色空间进行逆变换,就得到融合后的图像。如IHS(Intensity, Hue, Saturation)变换法先将原多光谱信息看作是RGB空间的颜色图像，对它进行IHS变换分别得到亮度通道I、色调通道H和饱和度通道S。之后用全色图像替代亮度通道I，再进行IHS逆变换从IHS空间变换到RGB空间，从而得到融合后的图像。基于颜色空间转换的方法实现原理简单，但是这种基于颜色空间转换的方法存在着两个方面的问题：(1)一般只适应于三通道图像融合；(2)虽然用全色图像直接替代了亮度通道，但是色调通道和饱和通道仍是原多光谱的信息的简单上采样，这必然会导致空间细节上的损失。

第二类是基于成分分析的方法[3,4,5]这类方法与颜色空间转换类似，不同的是它可以适用于任何波段的图像融合，这类方法先将多光谱的每个像素看成是一个多维向量，对其进行统计成分分析(如主成分分析)，得到投影向量,再将多光谱图像在这些投影向量上进行投影，在主成分投影的值保留了图像大部分的信息。然后用全色图像替换主成分图像，之后进行相应的反变换就可以得到融合图像。基于统计的主成分方法虽然可以进行任意波段图像的融合，但融合后的图像很难保持原多光谱图像的颜色信息（即发生颜色失真），而且在空间细节上与原全色图像相比也存在一定的损失。

第三类方法是基于小波分解法[6,7]，这类方法的基本思想是利用小波变换提取全色图像的高频信息（细节信息）和多光谱图像的低频信息（近似信息）。将通过小波变换提取的全色图像的高频信息和多光谱图像的低频信息组合成一组新的小波系数，然后对这些小波系数进行小波逆变换，从而得到融合图像。但是基于小波变换的图像融合当分解层数太少时，融合结果会存在明显的造痕迹，从而降低了融合图像的质量。当分解层数过多则会损失掉多光谱图像的颜色信息。

近年来，基于梯度场的图像编辑方法[8,9]在遥感图像融合方面得到了成功的应用。其基本思想是让融合图像保持全色图像的梯度，同时将低分辨率的多光谱图像看作是边界条件，并通过求解Poisson方程来得到融合结果。但是基于梯度场融合的方法由于其边界条件过于严格，使得融合图像对于多光谱图像的光谱信息存在一定损失，同时通过梯度算子保持细节信息过于简单，难以保持全色图像的所有细节信息。

综上所述，虽然现有的全色图像与多光谱图像融合方法很多，但这些融合方法很难在空间分辨率和光谱分辨率上同时达到最优。为了尽可能使得融合图像在空间分辨率与光谱分辨率上达到最优。本文在局部学习的基础上，对融合图像与全色图像的局部区域进行建模。具体而言，假设融合图像与全色图像在局部区域存在线性关系，对于每个局部区域，将回归损失函数表示为融合图像局部像素的二次拉普拉斯形式。通过对局部区域的损失函数进行累加，构建关于融合图像的全局图拉普拉斯。同时将多光谱图像看作是待融合图像的低分辨率表示。最后，构建总体目标函数。通过一定的转化，目标函数可以通过求解稀疏线性方程组得到闭合解。为了适应大尺寸图像融合，本文还提出了一种快速迭代的优化方法来求解融合图像。实验结果表明，本文所提出的融合方法相比于已有的算法能得到更高质量的融合图像。

2 基于局部学习的图像融合

设p、m1和y分别表示高分辨的全色图像，低分辨率的多光谱图像以及待融合图像。如图1所示，对于任意像素i所在的局部窗口Ni，假设全色图像p与待融合图像y在这个局部窗口满足：

其中yi中表示融合图像y在像素点j的像素值，pj表示全色图像p在像素点j的像素值，wi和bi表示局部线性模型的参数。

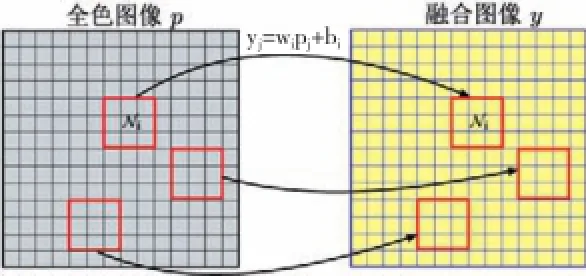
图1 局部线性模型示意图

在局部区域内，为了使得融合图像与全色图像满足上述线性模型，可以最小化如下局部窗口Ni内的正则化损失函数：

上式的第二项为正则化项，避免过拟合，其中，η表示正则化参数。对于整幅图像而言，对局部的损失能量进行累加，可得到全局损失函数为

最小化上式能量，使得融合图像与全色图像在所有局部区域能尽量满足局部线性关系。

对于多光谱图像m,我们将其看作是待融合y的低分辨率表示，即：

其中g_σ表示方差为σ的高斯函数，*表示滤波操作。设全色图像的分辨率是多光谱图像的n倍，根据尺度空间理论[10],σ可以根据以下公式来计算来确定：

最小化式(5)可以使得融合图像尽量满足等式(4)。

因此，对于图像融合来说，其目标为最小化(3)和(5)的整体能量。下一节我们将构建图像融合的总体目标函数，并提出两种不同的求解方法对目标函数进行优化。

3 目标函数优化

结合式(3)和(5)，图像融合的目标为最小化如下所示的能量函数：

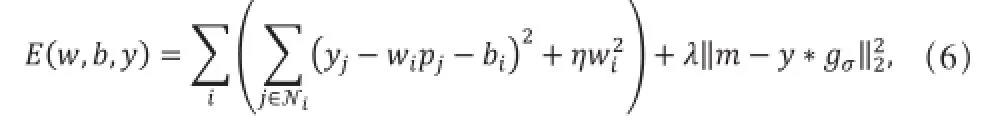
其中，λ表示权重因子。接下来的两小节将分别给出两种不同的方法来最小化上式目标函数(6)。

3.1 闭合求解

为了求解融合图像y，E(w,b,y)对w,b求导，并令其为0，可求得wi和bi分别为：

式中，Ni表示局部窗口Ni内像素的个数，为全色图像p在局部窗口Ni内的像素所组成的向量为待融合图像y在局部窗口Ni内的像素所组成的向量。设(I为单位矩阵)为Ni×Ni的中心化矩阵,(即 pi为pi中心化后的向量)。将式(7)和(8)代入式(6)，那么公式(6)的第一项可以写为如下形式：

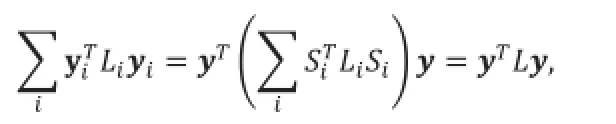
再考虑式(6)的第二项，由于滤波操作为线性操作，可以表示为稀疏矩阵-向量乘法的形式[13]，这里假设高斯滤波核gσ对应的稀疏矩阵表示形式为G。通过消除变量w,b后，图像融合的目标函数为：

式(10)的优化问题是关于y的二次型，那么其全局最优解可以对y求导并令其为0得到，即等价于求解以下稀疏线性方程：

(L+λG^TG)y=λG^Tm.

3.2 快速迭代求解

采用上述方法消除中间变量w,b，使得目标函数的优化等价于求解线性方程组。这种求解方式可以得到精确的闭合解。但是这种求解方法的计算代价过大。假设融合图像的大小为M×N，局部窗口的大小为ω×ω，那么构造拉普拉斯矩阵L的计算复杂度为：O(MNω6)，当图像尺寸较大时，构造矩阵L的复杂度过高。同时，虽然矩阵L为稀疏矩阵，但其大小为MN×MN，且每行的非零元素个数为(2ω-1)2。因此，当图像尺寸较大时，存储矩阵L这样一个大规模的稀疏矩阵所占用的内存仍然很大。

这说明第3.1小节的闭合求解方法存在两个方面的问题。一方面由于构建拉普拉斯矩阵的复杂度较高，使得求解速度仍然较慢，另一方面，当图像比较大时，稀疏矩阵L需要占用大量的内存资源。因此，闭合求解的方法不适应于大幅面图像的融合。为此，我们提出一种快速的迭代求解方法。

首先，我们可以将方程(6)写为如下积分形式：

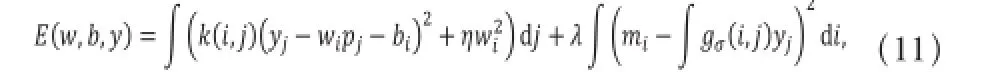
式中，k(i,j)表示一个窗口函数，假设窗口大小为3×3，那么k(i,j)的取值是：当像素j在3×3窗口内部时k(i,j)=1，否者为0。为了后续计算方便，将k(i,j)的值进行归一化，使其求和等于1，即k(i,j)=1/9。

可以采用类似EM的交替迭代方法，来最小化目标函数(11)。

（1）固定y，求解w,b。

利用变分法，式(11)对w,b求导并令其为0，可得：

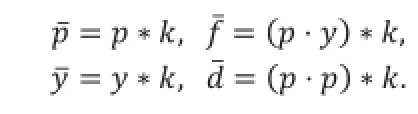
式中，由于滤波核k的元素都相等，因此，上述的滤波操作可以采用积分图像的技巧[14]进行加速。

（2）固定w,b，求解y。

式(11)对y求导，并令其为0，可求得：

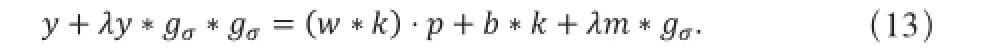
直接求解方程(13)比较困难，这里我们将其转换到频率上进行求解。方程(13)两边同时进行快速傅立叶变换可得：

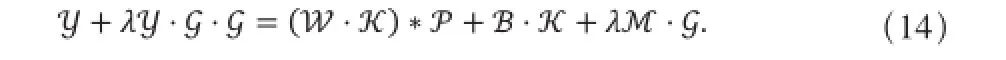
式中，Y,P,M,W,B分别表示y,p,m,w,b的傅立叶变换，G,K分别表示滤波核gσ,k的傅立叶变换。通过式(14)求得Y为：

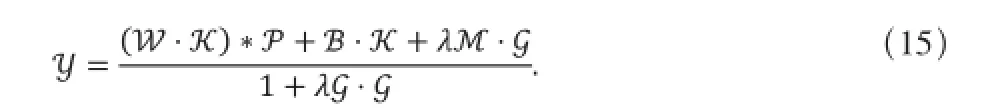
对Y进行傅立叶逆变换就可求得y。

重复上述两个步骤直到算法收敛。由于交替迭代的优化方法只能保证局部最优，因此其最终解依赖于初始值y的给定，对于全色图像与多光谱图像融合来说，多光谱图像m是y的一个非常好的初始解，因此y的初值设定为多光谱图像m。

4 实验结果及分析

为了验证本文融合算法的有效性，本节将进行高分辨率全色图像和低分辨率多光谱的融合实验。在本节实验中，本文所提出的融合算法的参数设置为：局部窗口大小为33，局部线性回归的正则化参数η=10-4。首先，我们与Poisson融合方法做比较，图2和3表示在QuickBird与LandsatETM+卫星图像上的融合结果。图2为2.4米多光谱与0.6米全色图像融合的结果（为了体现融合的对比效果,对多光谱图像进行了一次下采样），图3为30米多光谱与15米全色图像的融合结果。从图2（注意红色矩形框所标注的图像）和图3可以看出本文所提出的图像融合方法在光谱保持和空间细节上要明显优于Poisson融合方法。

图2 与Poisson融合的比较

图3 与Poisson融合的比较

为了定量评价本文所提出融合方法的性能，本文通过对融合图像与原始全色图像和多光谱图像进行比较来评价融合方法的有效性。本文从两个方面来评价融合图像：图像空间细节的保持度和光谱信息保持度。空间细节的保持度通过计算融合图像与全色图像的高频信息的差异来度量，即：

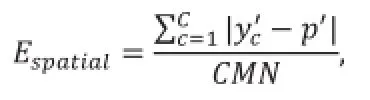
其中，c表示第c个波段，C为波段数，M,N为图像尺寸，y'c,p'分别表示融合图像和全色图像的拉普拉斯响应。光谱信息的保持度通过计算融合图像的低分辨率图像与多光谱图像之间的差异来度量，即：

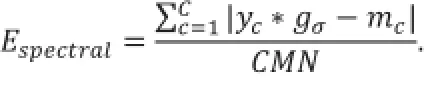
图4 本文融合方法与Poisson

图4表示本文所提出的融合方法和Poisson融合在图2和3所计算得到的平均E_spatial和E_spectral。从图4可以看出本文所提出的方法在空间细节和光谱保持度上都要明显由于Poisson融合，而快速迭代求解算法与闭合求解方法的差异非常小，这说明迭代求解算法在快速求解的同时，融合效果与闭合求解方法基本一致。

除了Poisson融合相比较外，本文还与一些传统的融合方法进行了比较，包括：IHS、PCA、Brovey变换、小波变换（这里采用db4小波进行4层分解，并将多光谱图像小波变换的近似信息与全色图像小波变换的细节信息进行组合，再进行小波逆变换）。

为了客观评价融合方法的有效性，我们采用文献[15]中所提出的方法，先对原始多光谱图像和全色图像都进行尺度退化，并将原多光谱图像作为参考图像。通过计算融合图像与参考图像之间的均方根误差(root-mean-squareerror,RMSE),相关性系数(correlationcoefficient,CC),相对均值偏差(AbsoluteMeanofBias,AMB)来评价融合方法的性能。图5为各种融合方法在2米多光谱与0.6米全色图像上的融合结果。表1为各种融合方法在图5所得结果的平均指标。从表1的各种指标可以看出，本文所提出的融合方法具有最小的RMSE，最大的CC以及最小的AMB，这说明本文方法相比于其他方法具有更好的融合效果。同时注意到迭代求解的方法与闭合求解方法的性能指标非常近似，这说明迭代求解的方法不仅与闭合求解法相当的融合效果。

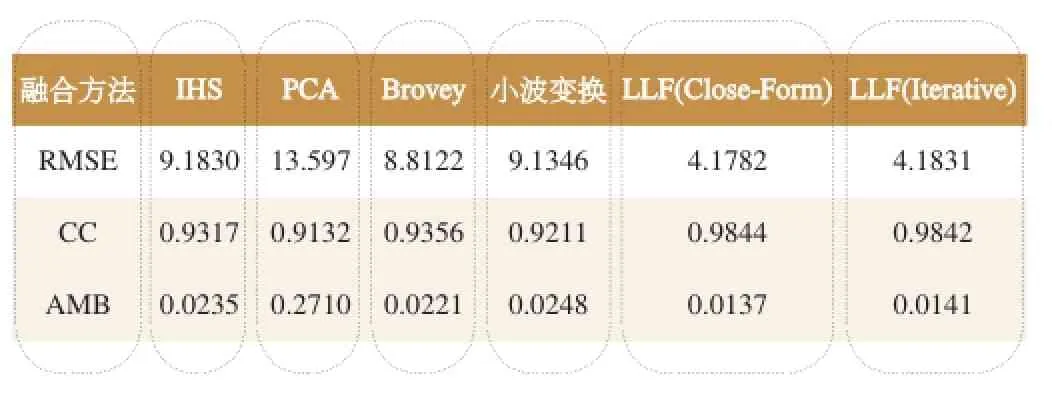
表1 图5中各种融合方法的RMSE, CC和Bias

5 总结

本文提出了一种基于局部学习的遥感图像融合方法。该方法一方面利用局部学习方法使融合图像保持全色图像的流形结构。另一方面将多光谱图像看作是融合图像的低分辨率表示。结合这两方面构建图像融合的目标函数，目标函数的优化可以通过求解稀疏线性方程组来得到闭合解，同时为了提高求解效率，本文还提出了一种快速迭代的求解方法。实验结果表明，本文所提出的融合方法相比传统融合方法具有更好的效果。同时，本文所提出的快速迭代算法将多光谱图像作为初始解，只需要少量的迭代次数（实验中一般小于10次）就达到稳定解。特别地，对于融合一幅1024×1024的图像而言，快速迭代求解方法一般只需要1秒左右的时间就可以得到与闭合求解（10秒）相当的融合结果。

图5 各种融合方法在QuickBird图像上的结果

[1] C. PohlandJ. V. Genderen. Multisensorimagefusioninremotesensing: Concepts, methodsandapplications[J]. InternationalJournalofRemoteSensing, 1998 (19) 5, 823-854

[2] Z. Wang, D. Ziou, C. Armenakis, D. Li, Q. Li.Acomparativeanalysisofimagef usionmethods[J]. IEEETransactionsonGeoscienceandRemoteSensing, 2005 (43) 6, 1991-1402

[3] F. A. Al-Wassai, N. Kalyankar, andA. A. Al-Zuky. TheIHStransformationsba sedimagefusion[J]. JournalofGlobalResearchinComputerScience, 2011 (2) 5.

[4] G. Simone, A. Farina, F. C. Morabito, S. B. Serpico, andL. Bruzzone. Imagefusi ontechniquesforremotesensingapplications[J]. InformationFusion, 2002 (3) 1, 3-15. [5] J.Sun, Y. Jiang, S. Zeng. AstudyofPCAimagefusiontechniquesonremotesensi ng. inProceedingsoftheSPIEInternationalConferenceonSpaceInformationTechno logy. 2005.

[6] H. Li, B. Manjunath, S. Mitra. Multi-sensorimagefusionusingthewavelettrans form. inIEEEInternationalConferenceImageProcessing.

[7] 晁锐, 张科, 李言俊. 一种基于小波变换的图像融合算法[J]. 电子学报, 2002 (32) 5, 750-753.

[8] J. Wen, Y. Li, H. Gong.Remotesensingimagefusionongradientfield.inProceedi ngsofthe18thInternationalConferenceonPatternRecognition (ICPR04) .

[9] Z. Zhou, S. Peng, B. Wang, Z. Hao, andS. Chen.Anoptimizedapproachforpan sharpeningveryhighresolutionmultispectralimages. IEEEGeoscienceandRemote SensingLetters.

[10] T. Lindeberg. Scale-SpaceTheoryinComputerVision. Norwell. MA, USA: KluwerAcademicPublishers, 1994.

[11] S. Xiang, F. Nie, C. Pan, C. Zhang.RegressionreformulationsofLLEan dITSAwithlocallylineartransformation. IEEETransactionsonSystems, Man, andCybernetics, PartB: Cybernetics, vol. 41, no. 5, pp. 1250–1262, 2011.

[12] A. Levin, D. Lischinski, Y. Weiss. Aclosed-formsolutiontonaturalimagematt ing. IEEETransactionsonPatternAnalysisandMachineIntelligence.

[13] Y. Wang, H. Yan, C. Pan, S. Xiang. Imageeditingbasedonsparsematrixvectormultiplication. in2011IEEEInternationalConferenceonAcoustics, SpeechandSignalProcessing (ICASSP) .

[14] F. C. Crow. Summed-areatablesfortexturemapping. inProceedingsofthe11th AnnualConferenceonComputerGraphicsandInteractiveTechniques.

[15] L. Wald, T. Ranchin, M. Mangolini. Fusionofsatelliteimagesofdifferentspati alresolutions: Assessingthequalityofresultingimages. Photogrammetricengineeri ngandremotesensing, 1997.

高东生，南京航空航天大学信息工程学院电力与通信工程专业硕士研究生，主要研究方向为遥感图像处理。

王颖，中国科学院自动化研究所助理研究员，主要研究方向为遥感图像处理、模式识别和计算机视觉。

更正声明

刊登在《自动化博览》杂志2013年12月刊第77页的张萍的作者简介中“甘肃宁夏人”有误，应为“宁夏银川人”。特此声明。

Remote Sensing Image Fusion Based on Local Learning

This paper presents a local learning based method for remote sensing image fusion. The key idea of our method is to construct the local linear model between the panchromatic image and the fused image in local region. Compared with the complexity in global region, image data in local region are much simpler. This means that local model is more reasonable than global model. Based on local learning, the regression error between the panchromatic image and the fused image can be formulated with Laplacian quadratic form, which makes the fused image preserve the manifold structure of the panchromatic image. In order to preserve the properties of the multispectral image, we build the scale space relationship between the fused image and the multispectral image via scale space representation. Consequently, the objective function of our model is proposed by combining the Laplacian quadratic form and the scale space representation. Meanwhile, a close form solution method and a fast iterative method are proposed to optimize the proposed model. Experimental results demonstrate the effectiveness of our model in comparison to the state-of-the-art methods.

Local Learning; Remote Sensing Image Fusion

B

1003-0492(2014)01-0086-05

TP212