地质力学磁力模型试验中均匀梯度磁场的构建

毕金锋，罗先启，沈 辉

（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

1 引 言

从20 世纪初起步至今，无论是在结构方向还是岩土方向模型试验都得到了广泛的发展和应用。地质力学模型试验根据相似理论，对特定工程问题进行岩土体的变形特性及破坏机制进行缩尺研究的方法[1]主要包括常规模型试验、土工离心模型试验[2]以及渗水力模型试验方法[3]。每一种方法都存在着一定的缺点与不足，如常规模型试验方法无法使试验模型的体力提高，离心机模型试验成本高昂，渗水力模型试验只适用于饱和土体等。

为了克服以上试验方法中的不足，罗先启等[4-6]提出了地质力学磁力模型试验方法，利用磁力场与重力场的相似性对铁磁材料与岩土体的混合材料进行加载，以达到模拟n 倍重力场的效果，并对地质力学磁力模型试验的相似理论、相似材料、梯度磁场以及应用[7]进行了一系列的研究，其中均匀梯度磁场的构建是地质力学磁力模型试验的关键问题之一，是通过磁力场模拟重力场的必要条件。

磁场的获取方法主要包括永磁方法、电磁方法、永磁和电磁相结合的方法。在地质力学磁力模型试验中不需要永磁体来维持一个恒定的磁场，为了在试验过程中方便对磁场大小的调节，使用电磁方法获取所需磁场。将Helmholtz 线圈之一的电流反向，可以产生磁通密度梯度相对均匀的磁场[8]，但这种方法适用于对永磁材料的加载，且由于Helmholtz线圈对线圈尺寸及线圈距离的要求，造成其设备尺寸和试验空间上的限制。对软磁材料的加载不仅要求磁通密度梯度的均匀性，还要求磁通密度方向保持相同。唐凯等[6]对单圆台线圈及双圆台线圈所产生的磁场进行了研究，然而并没有利用铁磁材料形成闭合回路，其产生的磁通密度梯度量值并不高，且磁通密度梯度的均匀性也不够，很难在地质力学磁力模型试验中提高铁磁材料所受磁力与其自身重力的倍数。

本文根据地质力学磁力模型试验中所需磁场的特点，利用构建磁路的基本原理，分3 种情况进行磁路分析，以提高磁通密度梯度的均匀性及其量值。对比结果表明，半开放式磁路得到的结果最理想，适合作为磁场发生装置应用于地质力学磁力模型试验中。

2 构建均匀梯度磁场的电磁学原理

铁磁材料在磁场中受力公式为

式中：V为磁性物质的体积；Ms为饱和磁化强度；B为所处磁场的磁通密度；α为受力方向。

由式（1）可以看出，铁磁材料受力与磁通密度梯度成正比，若使铁磁材料沿某一方向受力大小均匀，则其所处空间的磁通密度梯度应沿该方向上处处大小相等。

根据比奥-萨伐尔定律，可以计算通电线圈周围磁场的分布，即

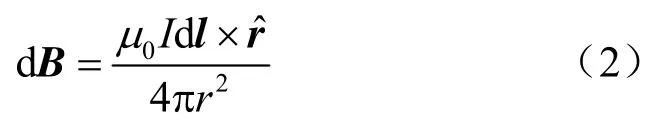
式中：μ0=4 π×10-7H/m为真空磁导率。

对于任意已知线圈分布情况的螺线管，沿电路第一小段电流积分，可以得到空间中任意位置的磁通密度B。然而，通过手算很难在已知螺线管形式的情况下计算出轴线以外任意点处的磁通密度[9]。

磁通密度B 与磁场强度H 和磁化强度M 存在关系：

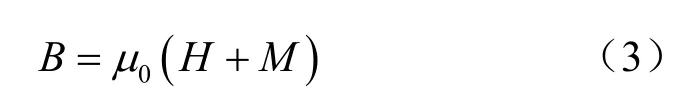
式中：M=χH，χ为物质的磁化率。定义相对磁导率 μr=1+χ，则式（3）可写为

电工纯铁和低碳钢是磁路中最常用的软磁材料，低碳钢的性能虽比电工纯铁略逊色，但低碳钢的成本低于电工纯铁[10]，考虑到在地质力学磁力模型试验磁场发生设备体积庞大、所需材料较多，采用低碳钢作为磁路材料，低碳钢B-μr曲线如图1所示[11]。通过式（4）计算得到初始磁化曲线如图2 所示。

图1 低碳钢的B-μr曲线Fig.1 B-μrcurve of low-carbon steel

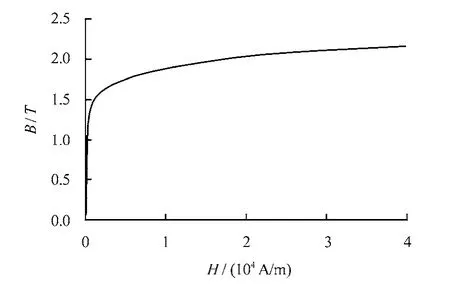
图2 低碳钢的初始磁化曲线Fig.2 Initial magnetization curve of low-carbon steel

由于磁体本身的工作状况非常复杂，目前对于一个已知磁路可以通过数值模拟计算出空间磁通分布，但根据空间磁通分布尚不能计算出惟一的最佳磁路，因此，构建磁路过程需要一些假定条件简化计算。为了将电路中的基尔霍夫第一、二定律应用于磁路中，假定磁路中没有漏磁，得到磁路的2个基本方程：

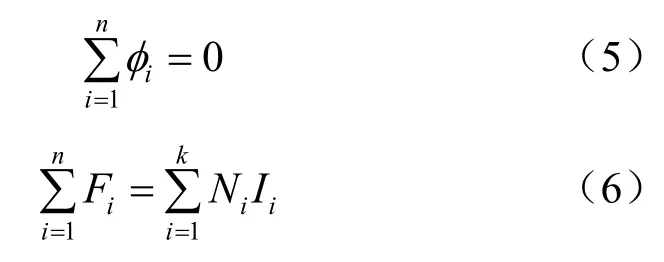
式（5）表示，对于任意包围着某一部分磁路的闭合曲面，通过该曲面的总磁通∑φi为0。式（6）中定义，围绕磁路的电流Ii与匝数Ni的乘积NiIi为线圈产生的磁通势，用Fi表示。某一段磁路中的磁场强度H 与磁路长度L 的乘积为该段磁路的磁势差。由此可以得到

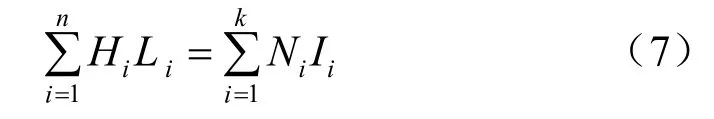
一般情况下，取磁路的几何中心线作为平均磁路长度L。

类比电路中的电阻，定义Rm=F/φ为磁阻，假定磁路中的材料是均匀的、线性的，可得

式中：μ为磁导率。进而

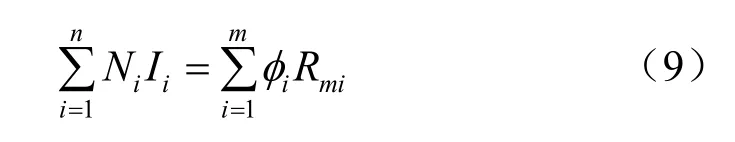
通过式（7）和式（9）两种方法可以计算磁路中螺线管所需的安匝数。

3 不同形式磁路电磁参数的确定

设计地质力学磁力模型试验磁场发生装置，不仅要考虑到所需磁场的梯度均匀性，还需要综合考虑占用空间、场地要求、重量、造价以及测试手段等方面的限制因素，然而各因素间相互制约，很难使每个方面都达到最佳效果。由图1 可以看出，低碳钢的饱和磁通密度约为2 T，此时H 的值达30 000 A/m 以上，需要很高的安匝数来维持该值，所以，应使H 值尽量小，同时B 值尽量大，即μr取最大值附近时最节约能源。

下文以试验空间为半径0.3 m、高0.6 m 的柱形为标准，对开放式、半开放式和封闭式3 种形式的磁路进行对比分析，以获得一种相对优化的结果，作为地质力学磁力模型试验的加载装置。

3.1 开放式磁路

开放式磁路即整个试验空间与线圈分离，通过磁路将磁场引入到试验区内，利用极靴的大小，使试验区内的磁通密度产生梯度。实际上，漏磁不可避免，在预定的试验区边缘处磁场分布不如预期的理想，为了保证试验空间的磁通密度梯度均匀性，设计试验区略大于所需要的空间大小，选择合适的范围进行试验。

为了减小螺线管对试验区磁场分布的影响，将4个相同螺线管对称布置在试验区周围，如图3 所示。图中，1 区为试验区，为一个上下底面半径分别等于0.3 m 和0.6 m 的倒立圆台；2 区为通电螺线管；3、4 区为极靴。理论上，当整个磁路回路的截面面积相同时，最节约能源，同时兼顾造价与重量的因素，磁路各部分尺寸见图3。ABCD 代表磁路的一个回路的4个节点，其中C、D 两点分别处于上下两极靴的几何中心，等效长度和等效面积按表1 取值。计算时，上下极靴为圆形，等效长度取LE=R/2，等效面积取为 SE=d2π(R/2)，d为极靴厚度。

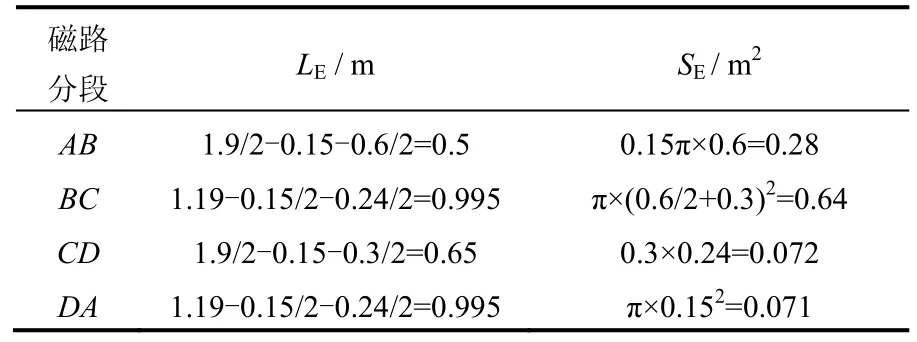
表1 开放式磁路ABCD 各段等效长度及等效面积Table 1 Length and area of open type magnetic circuit

假设在试验区底部的磁通密度Bb=1.6 T，磁通量φb=SbBb=0.452 Wb，忽略漏磁，试验区顶部磁通密度 Bt=φb/St=0.4 T。此时试验区上下的磁通密度差值为1.2 T，磁通密度梯度为1.5 T/m，可将低碳钢加载到其自身重力的30 倍左右。若试验材料中的散体铁磁材料所占体积百分比为33%，根据等效磁阻的方法可计算出铁粉与土体混合物等效相对磁导率μre=1/3μrFe+2/3μrSoil≈1/3μrFe，近似取为500。磁路各段的磁通量、磁通密度、磁场强度和所需要安匝数计算结果见表2。BC 段取整个试验区高度范围内的平均值，AB、AD 和CD 段 φAB=φAB=φAB=φb/4。磁场强度在已知磁通密度时可由图1、2 获得。

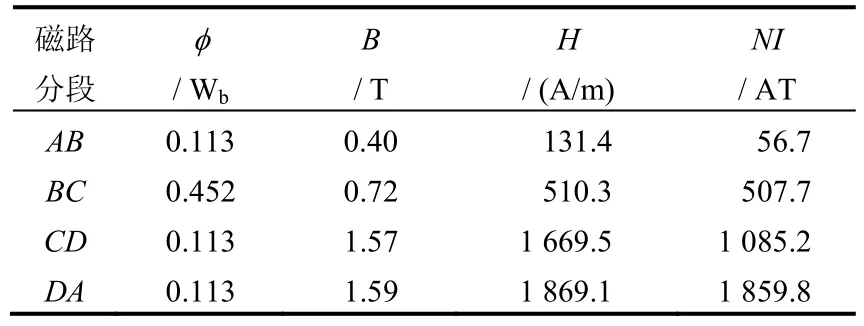
表2 开放式磁路磁场参数Table 2 Magnetic field parameters of open type circuit

由式（7）得到开放式磁路所需总的安匝数NItot=4NIAB+NIBC+4NICD+4NIDA=12 514.3 AT（Ampturn），平均分配到4个螺线管，每个螺线管所需要的安匝数NI=NItot/4=3 128.6 AT，取3 200 AT。

3.2 封闭式磁路

封闭式磁路中，将磁路设置在线圈外部，试验区设置在线圈内部，通过线圈大小的变化产生磁通密度梯度。

在假设没有漏磁的情况下，磁通量Φ 值在第一个试验区横截面上为定值，若保证磁通密度梯度dBz/dz=C1，则Bz=C1z+C2，即 Φ/S=C1z+C2，由此可得z 与线圈半径的关系为

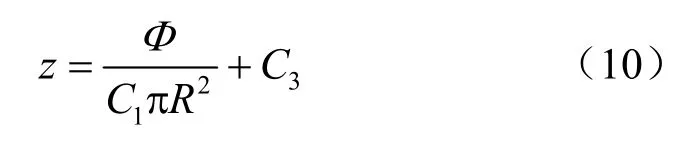
参照开放式磁路参数，取试验区内截面最小位置的半径为0.3 m，B=1.6 T，试验区梯度C1=1.5 T/m，则Φ=0.452 Wb，定义试验区截面最小处的线圈圆心为原点，由此计算得到线圈高度与半径的关系应满足：

按式（7）计算结果设计线圈形状，取试验区高0.8 m，底部、顶部对应的线圈半径分别为0.3、0.6 m。图4为装置剖视图，图中，1 区为试验区；2 区为线圈。

磁路ABCD 四段的等效长度和等效截面面积见表3，磁通量、磁通密度、磁场强度和所需要安匝数计算结果见表4。通过表4 可计算出需要的总安匝数为NItot=6 490 AT，取为6 500 AT。

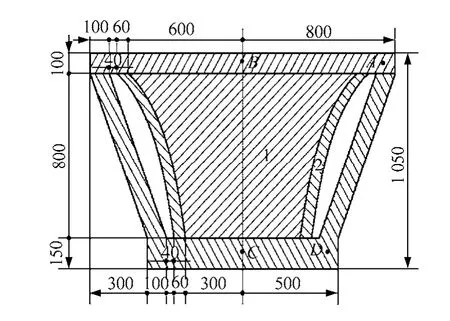
图4 封闭式磁路剖视图(单位:mm)Fig.4 Section view of closed type magnetic circuit(unit:mm)

表3 闭合式磁路ABCD 各段等效长度及等效面积Table 3 Length and area of closed type magnetic circuit

表4 封闭式磁路磁场参数表Table 4 Magnetic field parameters of closed type circuit

3.3 半开放式磁路

半开放式磁路是利用磁场在线圈端部的自然发散面产生的磁通密度梯度。磁路中存在空气隙，不能形成完整回路，图5为其剖视图。图中，1 区为试验区；2 区为线圈；3 区为空气隙；4为非铁磁性材料，可选橡胶或玻璃，置于线圈内部铁芯与上部试验区之间，有利于磁通密度均匀地进入试验区，厚度在图5 中未标注，按1 mm 计算。

在线圈端部，距离线圈越近，磁通密度的发散越快，为了使磁通密度能够沿试验区高度范围内均匀向外发散，需增加试验区与外部磁路之间的距离，所以将试验区下半部分设置为圆台形。

由于空气隙的存在，利用式（9）计算所需安匝数更为准确，为方便仍按式（7）计算，且假设：忽略从试验区顶端发散的少量磁通密度，所有磁通密度均从试验区底部进入，且从侧面均匀发散，经过空气隙3 区，返回磁路。

同样，假定试验区的磁通密度梯度为1.5 T/m，由于假设试验区顶部磁通密度为0，则试验区底部的磁通密度Bb=1.2 T，磁通量Φb=SbBb=0.603 Wb，磁路ABCDE 各段的等效长度和等效截面面积见5，磁通量、磁通密度、磁场强度和所需要安匝数计算结果见表6。

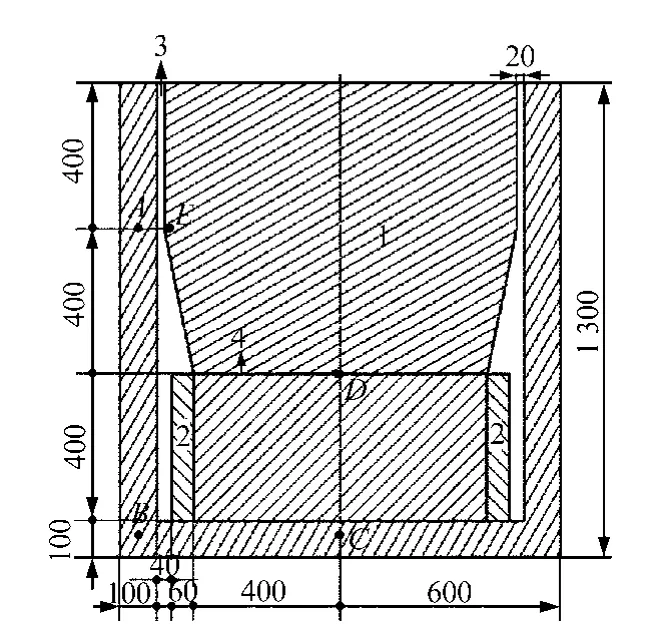
图5 半开放式磁路剖视图(单位:mm)Fig.5 Section view of semi-open type magnetic circuit(unit:mm)

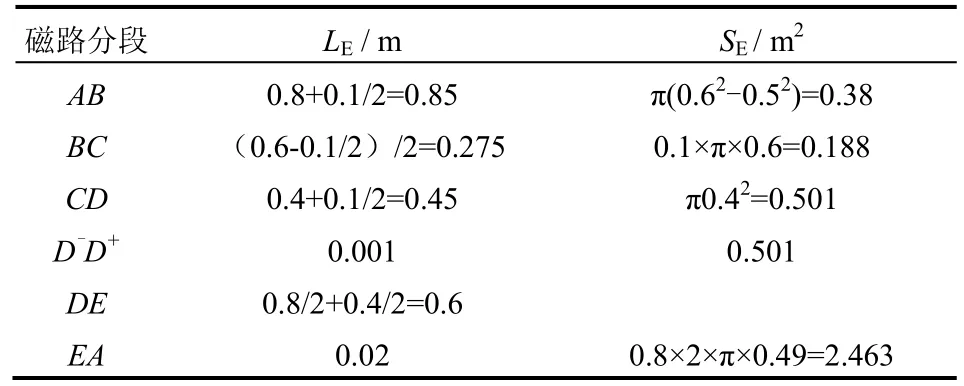
表5 半开放式磁路ABCDE 各段等效长度及等效面积Table 5 Length and area of semi-open type magnetic circuit

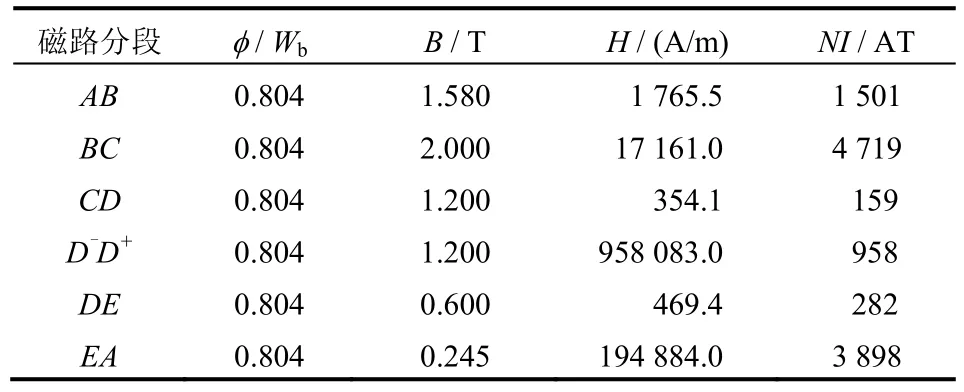
表6 半开放式磁路磁场参数表Table 6 Magnetic field parameter of semi-open type circuit

BC 段计算得到的B 值超过了饱和磁通密度，取为饱和值2 T，最终得到总需安匝数为NItot=11 517 AT，取为12 000 AT。

4 不同磁路的电磁特性

按章节3 得参数建立模型，应用有限元软件计算，3 种磁路形式下的试验区磁通密度分布情况如图6 所示。图中，白色实线为磁通密度等值线，等值线沿水平向越平直、沿竖直向分布越均匀，代表该区域的磁通密度梯度均匀性越好，所以选择黑色虚线框内范围作为半径0.3 m、高0.6 m 的最佳试验空间。

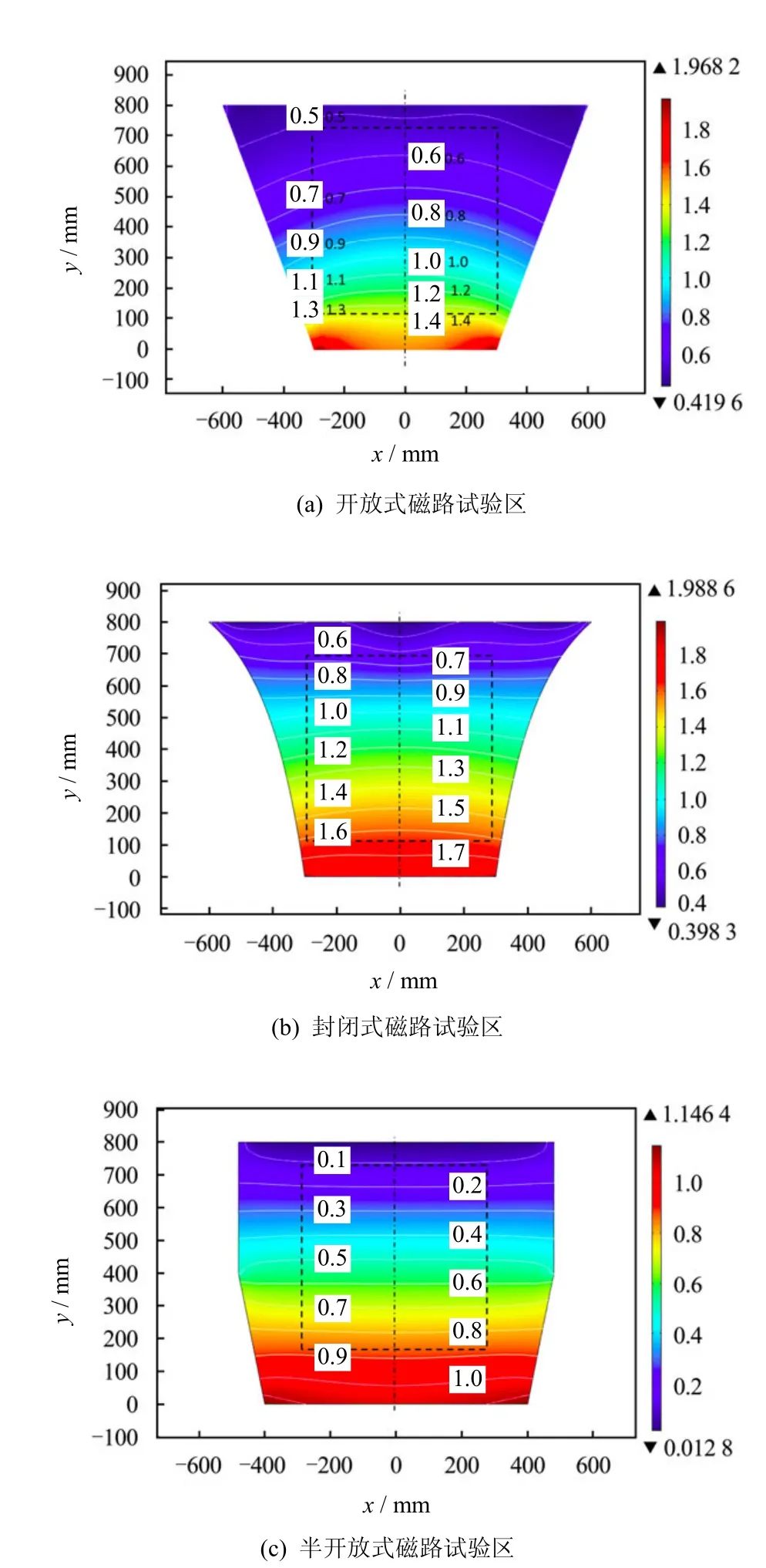
图6 磁通密度分布(单位:T)Fig.6 Magnetic flux density distribution(unit:T)

取最佳试验空间轴线及平行轴线且间距为0.1 m的4 条直线，对该组直线上磁通密度梯度进行分析，图7为3 种形式磁路的磁通密度梯度分布情况。由图可以看出，开放式磁路试验区的磁通密度梯度均匀性最差，试验区底部磁通密度梯度比上部高出近几倍。封闭式磁路的试验区底部的磁通密度梯度较差，并且在同一高度上沿半径方向梯度也较为分散。半开放式磁路最好，试验区上下端面梯度与均值相差在5%左右。并且在半开放式磁路中，4 条梯度曲线接近重合，可见在同一水平面上梯度值几乎相同。

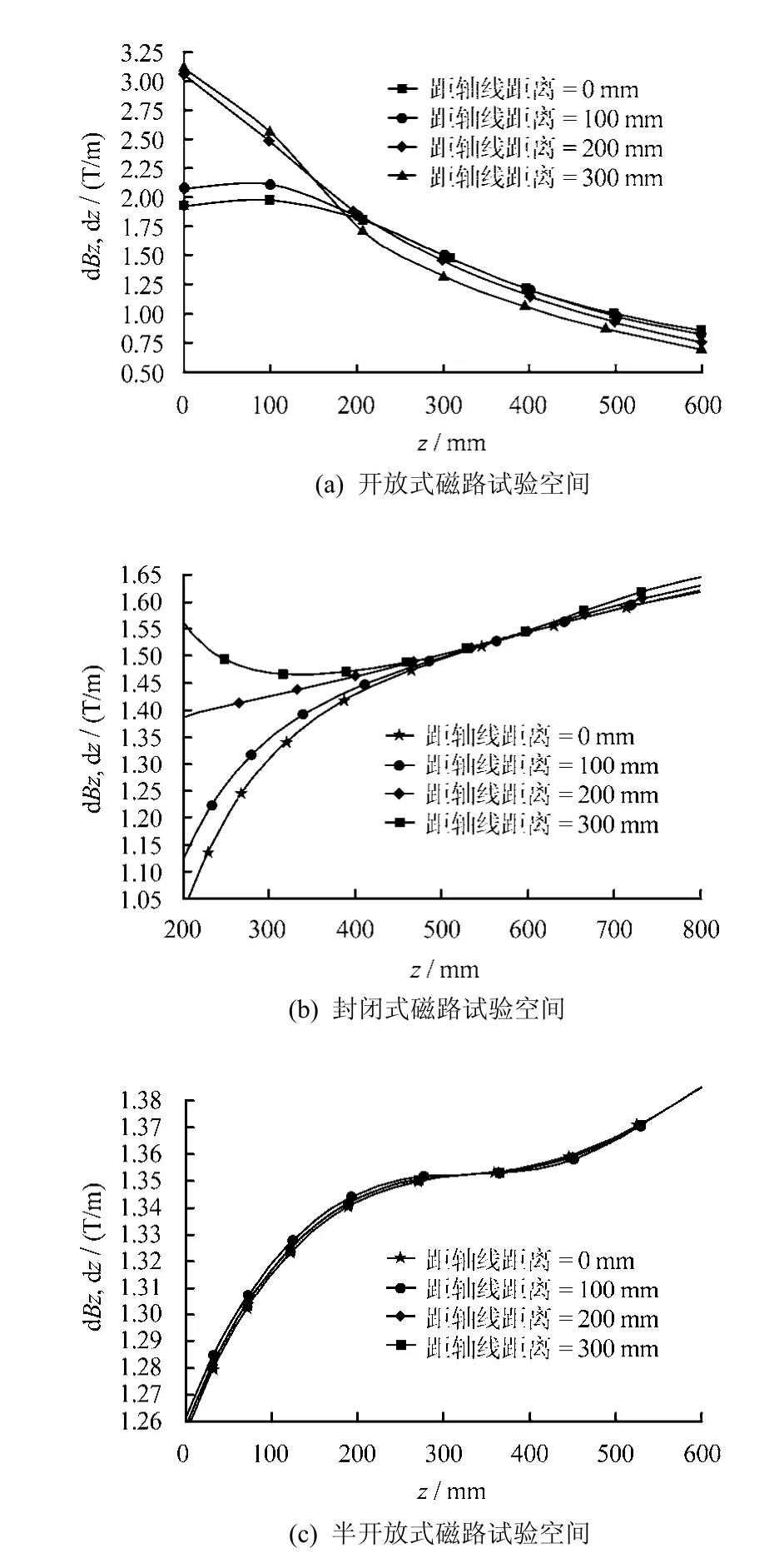
图7 磁通密度梯度分布Fig.7 Magnetic flux density gradient distrbution

在磁通密度梯度方面，半开放式磁路占据绝对的优势，但半开放式磁路也存在着一些不足之处，不计算试验区重量时，磁路里使用低碳钢的重量分别为：开放式磁路3.237 T，封闭式磁路4.838 T，半开放式磁路5.686 T，从而使半开放式磁路的造价略高。由于空气隙的存在，大部分能量储存于空气隙内，在维持相同量级的磁场时，半开放式磁路需要更大的磁势，造成能源的浪费。从测试方面考虑，开放式磁路的试验区完全暴露，便于测试仪器的放置，而封闭式试验区完全处于封闭状态，不利于直接观察到模型的位移和变形情况，半开放式磁路虽有磁路包围，不利于直接观察模型的变形，但是试验区周围存在空气隙，方便测试仪器的放置，同时试验区顶端没有磁路遮蔽，所以有利于后期考虑雨水作用时降雨系统的使用，可改造性优于另两种形式。由于封闭式磁路的螺线管形状的独特性，使其对制作工艺要求很高。将3 种形式磁路的性能进行对比，对比结果见7。

表7 不同形式磁路的性能对比Table 7 Performance comparison of different type circuits

综合表7 中各项性能指标的对比，在地质力学磁力模型试验中，如果没有相应的测试仪器与封闭式或半开放式装置相配套，则以牺牲精度为代价，采用开放式磁路；如果测试仪器可满足要求，则从节能和节约成本的角度而言，可采用封闭式磁路；如果要求保证磁通密度梯度的均匀性，或考虑后期对设备的改造，宜采用半开放式磁路。

5 结 语

地质力学磁力模型试验是一种利用电磁力加载的新型模型试验方法，要达到模拟重力场的效果，需要铁磁材料在磁场中受力均匀，即要求试验空间内的磁通密度梯度处处相等。

利用铁磁材料使整个磁场发生装置形成闭合回路，不仅可以充分利用螺线管产生的磁通量，还可以通过改变磁路的形式控制磁通密度的分布，从而使磁场尽可能接近试验要求的理想状态。构建开放式、封闭式、半开放式3 种形式的磁路，利用有限元软件进行数值模拟，得到3 种形式磁路的试验空间磁通密度及其梯度分布情况。

3 种形式的磁路各有其优点及缺点，但就磁通密度梯度的均匀性而言，半开放式磁路最佳，其最佳试验空间内的误差在5%以内，并且测试方法可采用光学或声学非接触位移测量方法对模型的变形特征进行测试，与能源的节约对比，试验结果的精确性更加重要，采用半开放式磁路作为地质力学磁力模型试验的加载装置更加合理。

[1]沈泰.地质力学模型试验技术的进展[J].长江科学院院报,2001,18(5):32-36.SHEN Tai.Progress of geomechanical model test technology[J].Journal of Yangtze River Scientific Research Institute,2001,18(5):32-36.

[2]黄志全,王思敬.离心模型试验技术在我国的应用概况[J].岩石力学与工程学报,1998,17(2):199-203.HUANG Zhi-quan,WANG Si-jing.The application general situation of centrifugal model test in China[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(2):199-203.

[3]方磊,李广信,黄锋.室内土工模型试验的新方法——桩基渗水力土工模型试验[J].高校地质学报,1997,3(4):451-457.FANG Lei,LI Guang-xin,HUANG Feng .A new method of geotechnical model test—Geotechnical model test of pile foundation water seepage force[J].Geological Journal of China Universities,1997,3(4):451-457.

[4]罗先启,程圣国,张振华,等.地质力学磁力模型试验相似理论研究[J].岩土力学,2011,32(4):457-462.LUO Xian-qi,CHENG Sheng-guo,ZHANG Zhen-hua,et al.Study of similarity theory of geomechanical model test inelectromagnetic field[J].Rock and Soil Mechanics,2011,32(4):457-462.

[5]罗先启,葛修润,程圣国,等.地质力学磁力模型试验相似材料磁力特性研究[J].岩石力学与工程学报,2009,28(增刊2):3801-3807.LUO Xian-qi,GE Xiu-run,CHENG Sheng-guo,et al.Study of magnetic material property of geomechanical model test in electromagnet field[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(Supp.2):3801-3807.

[6]唐凯,罗先启,张振华.地质力学磁力模型试验磁场梯度研究[J].三峡大学学报(自然科学版),2010,32(1):57-59.TANG Kai,LUO Xian-qi,ZHANG Zhen-hua.Study of magnetic field gradient in geomechanical model test[J].Journal of China Three Gorges University(Natural Sciences),2010,32(1):57-59.

[7]张振华,王幸林,唐凯,等.地质力学磁力模型试验技术应用于滑坡物理模型试验的可行性探讨[J].岩土工程学报,2012,34(7):1291-1298.ZHANG Zhen-hua,WANG Xing-lin,TANG Kai,et al.Feasibility of application of technology of geomechanical magnetic model tests to physical model tests on landslides[J].Chinese Journal of Geotechnical Engineering,2012,34(7):1291-1298.

[8]JILES D.磁学及磁性材料导论(第二版)[M].肖春涛译.兰州:兰州大学出版社,2003:18-20.

[9]PURCELL E M.Electricity and magnetism[M].New York:Mcgraw-Hill Book Company,1985:226-232.

[10]王以真.实用磁路设计[M].北京:国防工业出版社,2008:65-66.

[11]蔡国廉.电磁铁[M].上海:上海科学技术出版社,1965.