一种快速高精度的改进Fitz频率估计算法

王 芳，陈 勇，叶志清

(江西师范大学物理与通信电子学院，江西南昌330022)

0 引言

白噪声环境下复正弦信号的频率估计在雷达、声纳、数据测量、载波恢复、语音编码、感知阵列等领域有广泛应用，如何从N个离散采样点中求解信号的频率是信号估计领域一个热点问题.早在1974年，D.C.Rife等［1］就提出了频率估计方差可以达到克拉美劳下限(CRB)的最大似然(ML)频率估计方法.从统计学意义上讲，ML方法是性能最优的频率估计方法，但该算法计算复杂、速度慢、且不利于实时处理，一般很少直接采用ML估计.为实现快速高精度频率估计，国内外学者提出了很多次优的频率估计算法，本文将其归纳为以下的3种类型.

1)子空间类算法.此类算法中最具代表性的有:多重信号分类算法(MUSIC)［2］、子空间旋转不变算法(ESPRIT)［3］等现代谱估计算法.它们利用信号协方差矩阵的特征向量张成信号子空间和噪声子空间，从而得到频谱估计的几何解，其特点是频率分辨率高，但运算量大，不利于实时处理;

2)频域估计算法.此类算法通常采用FFT谱线内插的方法获得较精确的频率估计.D.C.Rife算法是对幅度最大的2根谱线的幅度进行内插，而B.G.Quinn算法［4］是对谱线幅度之比的实部进行插值.D.C.Rife算法与B.G.Quinn算法的计算量小，实现简单，但随着信号频率变化，其估计性能波动很大.尤其是在低信噪比下，对于某些特定的频率点，噪声会使得插值出现方向性错误而导致估计性能急剧恶化.MRife算法［5］通过人为引入一定的频偏，在一定程度上避免了出现插值方向性错误，但与此同时却大大增加了频率估计的时延，不适合对突发信号的频率估计;

3)时域估计算法.S.A.Tretter最早提出利用信号的瞬时相位进行频率估计［6］，其频率估计方差理论上可达到CRB.但实际上，瞬时相位只能在主值范围内测量，而在观测期间相位的变化范围一般远远超过2π，即在相位测量中存在模糊问题.S.Kay提出利用信号的相位差进行频率估计［7］，简单而有效地解决了相位模糊问题，但分析表明Kay算法的信噪比阈值较高.M.P.Fitz进一步提出不仅可以利用相邻采样点的相位差，还可利用相距较远的采样点的相位差［8］，即以自相关函数相位加权平均实现频率估计，在低信噪比时取得了较Kay算法更佳的频率估计性能，其信噪比阈值可达-10 dB，但付出的代价是频率估计范围减小［9］.M.Luise 等［10］提出的加权线性预测频率估计方法与Fitz算法的原理基本一致.

U.Mangali等［11］提出利用相关函数的相位差来估计频率，使频率估计范围大大增加，但计算量比Fitz法和LR法略大，且信噪比阈值在0 dB以上.

综上所述，子空间类算法的估计精度高但实时性差，频域估计算法的实时性强但估计精度不足，而时域估计算法，特别是Fitz算法，在实时性以及估计精度方面取得折中，因此在工程中获得广泛应用［12-15］.基于此，本文在Fitz算法的基础上，提出了一种基于修正自相关函数的改进Fitz频率估计算法.与Fitz算法相比，改进算法没有额外增加计算复杂度，但却进一步提高了频率估计精度，因此具有一定的工程实用价值.

1 Fitz算法与其性能分析

AWGN背景中的单一频率复正弦信号的观测序列可表示为

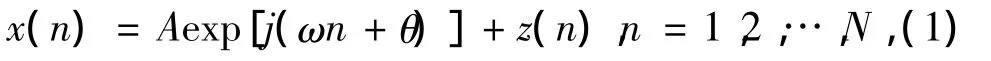
其中复正弦信号的幅度A、频率ω以及初始相位θ为确定参数，但大小未知.假设z(n)为0均值复白高斯噪声，z(n)=zr(n)+jzi(n)，其中zr(n)与zi(n)均为实高斯随机变量，其均值为0，方差为/2，且zr(n)和zi(n)之间不相关.定义信号x(n)的信噪比为 SNR=A2/.本文主要关注未知参数(A，ω，θ)中频率ω的估计问题，而对频率ω的最大似然估计等价于搜寻信号x(n)的周期图的最高峰，即

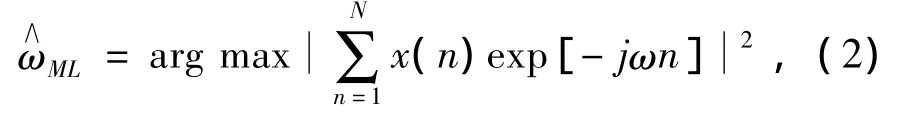
对(2)式中的似然方程关于频率ω求导数，令其结果为0，并经过简单整理后得

其中

为非归一化相关函数，(4)式中，［·］*表示求共轭.在无噪声的情况下，易知相关函数为R∧N(m)=K·exp［jωm］.在相关函数R∧N(m)的相位中正好包含了需要估计的频率信息，即arg{R∧N(m)}=mω，其中arg{·}表示求相位值.

假设信噪比足够高，可以得到如下的近似结果

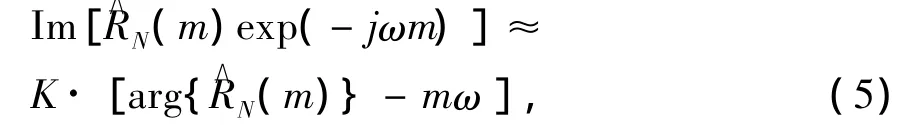
将(5)式代入(3)式得

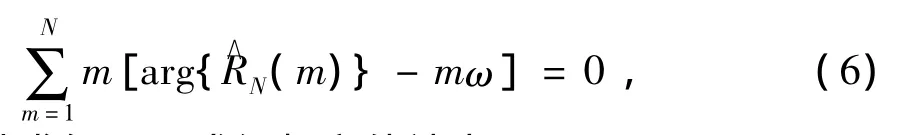
通过求解(6)式得频率估计为

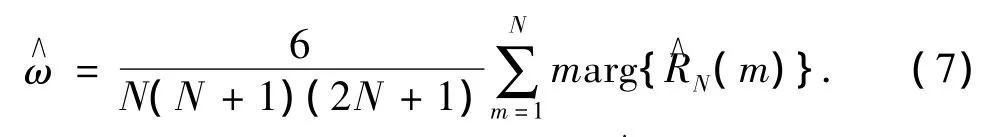
但为避免在求解相关函数R∧N(m)的相位时出现相位模糊问题，在(7)式中通常仅利用J项相关函数来估计频率ω，其中J≪N，则此时频率估计为

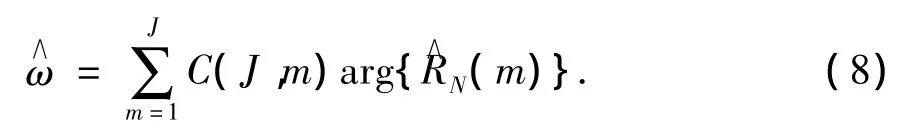
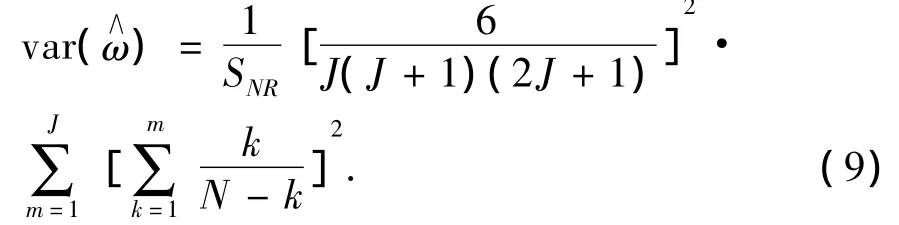
仿真分析同样表明，即使当信噪比足够大时，Fitz算法的频率估计方差仍然与CRB存在较大的差距.因此，Fitz算法的频率估计性能仍有待进一步提高.本文将自定义的修正自相关函数引入Fitz算法，提出了一种改进的Fitz算法.新算法不仅没有明显增加计算复杂度，即保留了时域频率估计算法的实时性强的优点，而且同时又取得了更好的频率估计精度.

2 基于修正自相关函数的改进Fitz算法

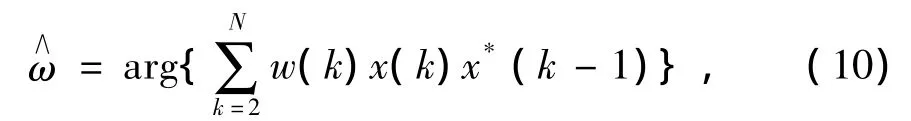
其中

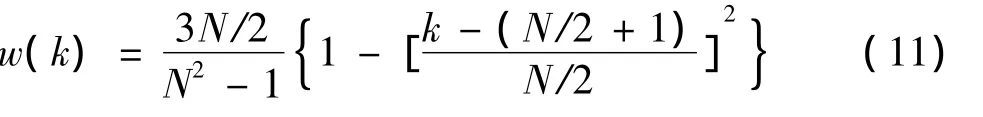
是使得WLP算法的频率估计方差达到最小的一组加权值，本文中简称为Kay窗函数.

仿真分析表明:随着信噪比的增加，UWLP算法的频率估计方差始终无法达到CRB，而WLP算法的频率估计方差却能够逐渐接近并最终达到CRB.导致出现上述差别的原因正是由于在计算自相关函数N(1)时，UWLP算法采用了均匀加权，而WLP算法采用了Kay窗函数加权.

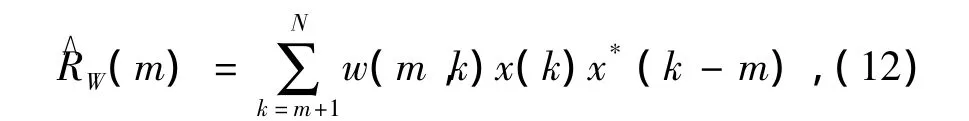
其中

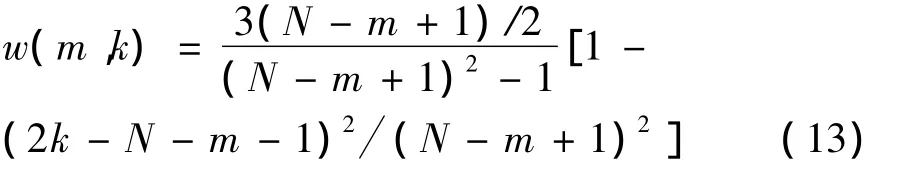
是对Kay窗函数w(k)的推广.特别地，当m=1时，w(m，k)等于Kay窗函数w(k)，因此不妨将w(m，k)称为广义Kay窗函数.改进的Fitz算法为

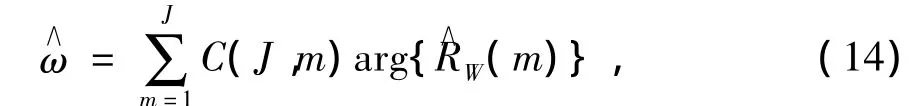
即通过计算修正自相关函数相位arg{R∧W(m)}的加权和得到频率估计值.

为方便起见，下文中将改进的Fitz算法简记为mFitz算法.对比(8)式和(14)式不难发现，mFitz算法相对于Fitz算法并未明显增加计算复杂度，但由于mFitz算法借鉴了WLP算法的思路，即在自相关函数时采用了广义Kay窗函数加权，因此有望取得较Fitz算法更佳的频率估计精度.文中的仿真分析证明了这一点.

基于修正自相关函数的mFitz频率估计器的结构图如图1所示.在实际应用中，假设信号x(n)的长度N已知，可以按照(13)式事先计算出所有的广义Kay窗函数系数w(m，k)，并保存在ROM存储器中.在利用mFitz算法估计信号频率时，直接查找相应的广义Kay窗函数系数w(m，k)即可，从而使得硬件实现系统(如DSP系统)的运算量进一步下降.

图1 改进的Fitz频率估计器

3 仿真分析

采用Monte-Carlo计算机模拟方法，对WLP、UWLP、Fitz、mFitz等时域频率估计算法进行了仿真分析.仿真条件为:数据长度 N=24，频率 ω=0.1π rad·s-1，信噪比从 -10 dB增加至40 dB，考虑3 种 J的取值情况即J=1，2，3，Monte Carlo计算机模拟次数为5000次.

图2给出了 Fitz算法的频率估计方差仿真结果.为方便对比不同仿真条件下的频率估计方差，图2及其它仿真图形中将方差大小以对数的形式表示，即10log(1/var()).图2表明:1)Fitz算法的频率估计方差随着信噪比增加而逐渐减小;2)J的取值越大，Fitz算法的频率估计方差就越接近CRB;3)当信噪比达到40 dB时，对应J=3的频率估计方差曲线与CRB之间仍然存在着约3 dB的差距.

图3对比了WLP算法与UWLP算法的频率估计方差.图3表明:随着信噪比的增加，UWLP算法的频率估计方差同样无法达到CRB;而WLP算法的频率估计方差能够随着信噪比的增加逐渐接近并最终达到CRB.

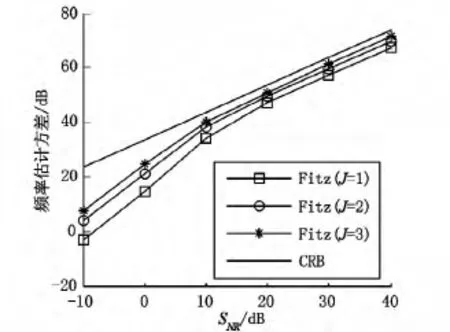
图2 Fitz算法的频率估计方差

图3 WLP与UWLP算法的频率估计方差

图4给出了当 N=24，ω=0.1π rad·s-1时mFitz算法的频率估计方差仿真结果，而图5仿真了当N=48，ω=0.2π rad·s-1时mFitz算法的频率估计方差.图4和图5表明:1)随着信噪比的增加，mFitz算法的频率估计方差逐渐减小;2)J的取值越大，mFitz算法的频率估计方差就越接近CRB;3)与Fitz算法不同，mFitz算法在信噪比足够高时，其频率估计方差能够逐渐接近并最终达到CRB.

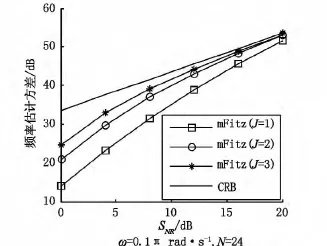
图4 改进Fitz方法的频率估计方差

图5 改进Fitz方法的频率估计方差

图6 时域频率估计算法对比

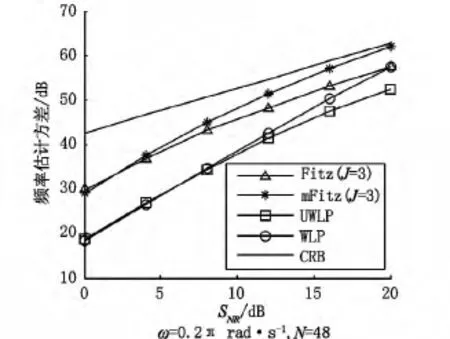
图7 时域频率估计算法对比

4 结论

时域频率估计算法具有实时性强与估计精度高等优点，已在工程中获得广泛应用.Fitz算法相对于其它时域频率估计算法具有较低的信噪比阈值，但分析表明当信噪比高达40 dB时，Fitz算法的频率估计方差仍然与CRB之间存在着较明显的差距.本文提出了一种改进的Fitz频率估计算法，首先定义一种广义Kay窗函数加权的修正自相关函数，然后计算修正自相关函数相位的加权和，最终得到复正弦信号的频率估计值.分析表明:1)改进Fitz算法相对于Fitz算法在频率估计方差方面有较明显的改善;2)改进Fitz算法的计算复杂度并未明显增加;3)在现有的时域频率估计算法中，改进Fitz算法在兼顾实时性的同时，取得了更高的频率估计精度，具有较好的工程实用价值.

［1］ Rife D C，Boorstyn R.Single tone parameter estimation from discrete-time observations［J］.Information Theory，1974，20(5):591-598.

［2］Schmidt R O.Multiple emitter location and signal parameter estimation ［J］.IEEE Transactions onAntennas and Propagation，1986，34(3):276-280.

［3］Roy R，Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques ［J］.Acoustics，Speech and Signal Processing，1989，37(7):984-995.

［4］ Quinn B G.Estimating frequency by interpolation using Fourier coefficients［J］.Signal Processing，1997，28(2):113-122.

［5］邓振淼，刘渝.正弦波频率估计的牛顿迭代方法初始值研究［J］.电子学报，2007，35(1):104-107.

［6］Tretter SA.Estimating the frequency of a noisy sinusoid by linear regression ［J］.Information Theory，1985，31(6):832-835.

［7］ Kay S.A fast and accurate single frequency estimator［J］.Acoustics，Speech and Signal Processing，1989，37(12):1987-1990.

［8］Fitz M P.Further results in the fast estimation of a single frequency［J］.Communications，1994，42(2/4):862-864.

［9］齐国清，吕健.基于自相关函数相位的频率估计方法方差分析［J］.大连海事大学学报，2007，33(4):5-9.

［10］Luise M，Reggiannini R.Carrier frequency recovery in alldigitalmodems for burst-mode transmissions［J］.Communications，IEEE Transactions on，1995，43(234):1169-1178.

［11］MengaliU，Morelli M.Data-aided frequency estimation for burst digital transmission ［J］.Communications，IEEE Transactions on，1997，45(1):23-25.

［12］Cui Yang，Gang Wei，Chen Fangjiong.An estimation-range extended autocorrelation-based frequency estimator［J］.EURASIP Journal onAdvances in Signal Processing，2009(10):961938.

［13］杨德钊，宋凝芳，林志立，等.基于自相关及相位差法的高精度频率估计算法［J］.北京航空航天大学学报，2011，37(8):1030-1033.

［14］ Fu H，Kam P Y.Sample-autocorrelation-function-based frequency estimation of a single sinusoid inAWGN［C］//IEEE 75thVehicular Technology Conference，Yokohama，2012:1-5.

［15］曹燕.含噪实信号频率估计算法研究［D］.广州:华南理工大学，2012.

［16］邹昕，叶志清.基于量子双向传态的多方量子通信网络的构建方案［J］.江西师范大学学报:自然科学版，2013，37(5):492-496.

［17］Lank G W，ReedI S，Pollon G E.A semicoherent detection and Doppler estimation statistic［J］.Aerospace and Electronic Systems，1973，9(2):151-165.

［18］吴柳雯，叶志清.用4粒子Ω纠缠态实现多粒子隐形传态［J］.江西师范大学学报:自然科学版，2013，37(6):561-564.