不同回收价格的闭环供应链收益分配问题研究

高举红 孟燕莎

（天津大学管理与经济学部 天津 300072）

0 引 言

随着对构建资源节约型、环境友好型社会要求的提高，环境问题越来越受到人们的普遍关注，企业在生产制造过程中也越来越重视对环境的伤害．产品回收再利用不仅可有效降低资源浪费等对环境的影响，也可帮助企业降低成本、树立良好的社会形象．闭环供应链作为一种新的供应链管理思想，在逐步引起国内外学者的关注［1－2］．

目前国内外有关闭环供应链的研究主要集中在闭环供应链的定价、逆向物流网络设计和库存控制等领域［3－5］．闭环供应链收益分配方面，Cattani等［6］研究了不同渠道下的批发价格策略，并通过价格实现了收益协调，体现了价格策略的重要性．郑鑫等［7］以合作博弈为研究方法，探讨了由制造商、第三方物流和零售商组成的三级闭环供应链收益分配问题；牟小俐等［8］在考虑到销售努力水平对市场需求量和回收量的影响下，讨论了不同合作方式下，由制造商、零售商和第三方回收商构成的闭环供应链上各成员及联盟的最优价格策略与收益；易余胤［9］在研究不同市场力量下再制造闭环供应链的决策时建立了由1个制造商、2个竞争零售商构成的闭环供应链，但前提是2个零售商的回收价格一致．另外，刘伟华等［10］对基于物流服务组合的2级服务供应链的利润分配模型进行了研究；Shauhan等［11］研究了基于收益共享的供应商、零售商伙伴关系模型，并利用此模型分析了不同供应链成员的收益情况；张东堂等［12］基于Shapley值法探讨了包含供产销的三级供应链的联盟博弈和收益分配问题；马士华等［13］也利用Shapley值法解决了供应链合作伙伴间的收益分配．在此之后，施国洪等［14］、刘家国等［15］、吕培培等［16］考虑了包含2个零售商的供应链系统，并从零售商分散决策和集中决策2个方面对供应链的收益情况进行分析，得到两种情形下供应商、零售商以及供应链的整体收益函数，但研究仅限于正向供应链．

通过上述文献分析可见，对闭环供应链收益分配的研究大都集中在单节点单成员的层面，即使有考虑到增加节点成员的情况，也限于正向供应链或者节点上2个成员回收价格相同．本文将正向物流与逆向物流结合，使2个零售商以不同价格负责废旧产品的回收，利用博弈论相关知识，分别研究在零售商分散决策和集中决策情况下供应链各成员及整体的最优收益，并对结果进行比较分析．

1 问题描述

考虑由一个制造商、两个竞争零售商，且零售商以不同价格分别回收的两级闭环供应链系统（如图1），三者之间信息完全对称．制造商负责生产新产品和对回收的废旧产品进行再利用，2个零售商共同负责销售新产品和从消费者手中回收废旧产品．令M，R1，R2分别代表制造商和两个零售商，相应地∏M，∏R，∏R分别表示三者12的收益函数，则闭环供应链的整体收益为∏＝∏M＋∏R1＋∏R2．制造商利用新材料和回收材料生产单位产品的成本分别是cm，cr（cm＞cr），令θ＝cm－cr，表示因回收利用废旧产品而节约的成本．对理性决策者而言，零售商的产品售价高于从制造处的批发价格，制造商从零售商处回收旧产品的价格高于零售商从消费者处回收旧产品的价格．

2 收益模型构建

2．1 模型假设

假设1 制造商对废旧品再造后的产品和利用新材料生产的产品是同质的．

假设2 制造商与零售商之间完全信息对称，零售商分散决策时为非完全信息对称，集中决策时为完全信息对称．

假设3 闭环供应链各节点均为风险中性，即决策目标均为收益函数最大化．

假设4 零售商集中决策时，两个零售商平均分配二者联盟所得的收益．

2．2 零售商分散决策

零售商分散决策情况下（见图2），供应商以相同批发价格W 批发产品给两个零售商，两个零售商各自决定商品的市场价格P1，P2，分别对商品进行回收，且分别承担回收的固定成本C1，C2．假设回收价格分别是P3，P4，则P1，P2和P3，P4是零售商的决策变量；假设制造商以相同的回收转移价格W0从2个零售商处购买废旧产品，则W，W0是制造商的决策变量．

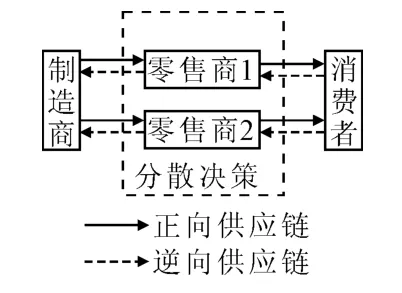
图2 零售商分散决策的闭环供应链系统

假设产品的市场需求函数为Di＝Di（Pi，Pj）＝Q－αPi＋βPj，i≠j且i，j＝1，2，表明产品的市场需求函数不仅与自身产品价格有关，还受竞争对手产品价格的影响．Q表示市场容量；α，β为常量，表示消费者对2个市场价格（P1，P2）的敏感系数，且α＞β＞0；用Di＝Di（Pi，Pj）＝N＋γPiεPj，i≠j且i，j＝3，4，表示废旧产品回收量；N表示当回收价格为0时废旧产品的回收量，体现了消费者的环保意识，N越大表明人们的环保意识越强；γ，ε为常量，表示消费者对两种市场回收价格的敏感系数，且ε＞γ＞0．

此时制造商和两个零售商的收益函数分别为

零售商分散决策下，制造商决定对两个零售商的统一批发价W 和回收价W0，目的是使自己的收益最大．由于此模型中存在两个零售商，导致零售商之间存在一种博弈关系．且零售零之间不存在信息沟通，是完全独立决策，此时二者的博弈过程可用古诺模型解释．故整个博弈的第一阶段就是两个零售商之间的博弈，二者分别决定自身的销售价格P1，P2和从消费者处回收废旧产品的价格P3，P4，以使自身收益最大化．由逆向归纳法解得：

将式（4）中各量分别代入式（1），可得

将式（5）中变量分别代入式（4），得

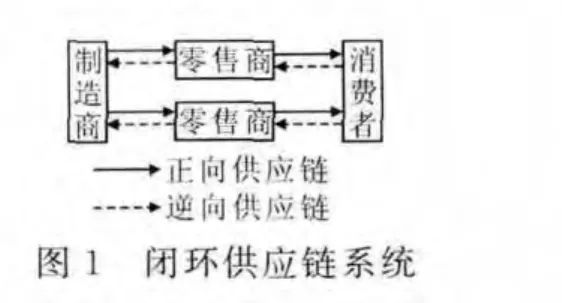
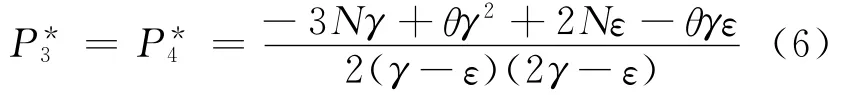
将式（5）、（6）代入式（1）－（3），得制造商和两个零售商的最优收益分别为：

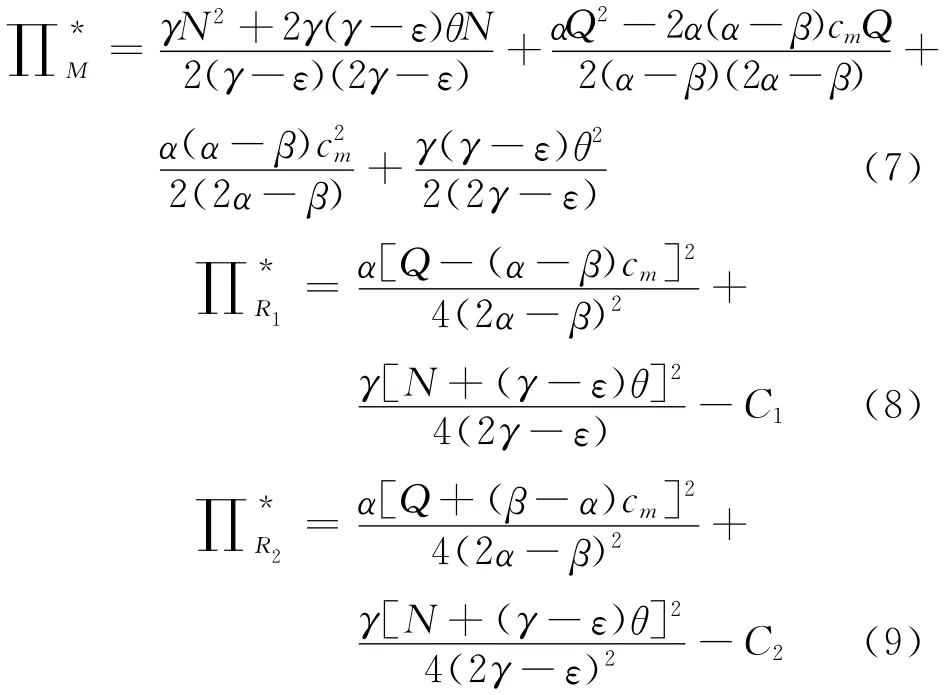
闭环供应链的总体收益为：

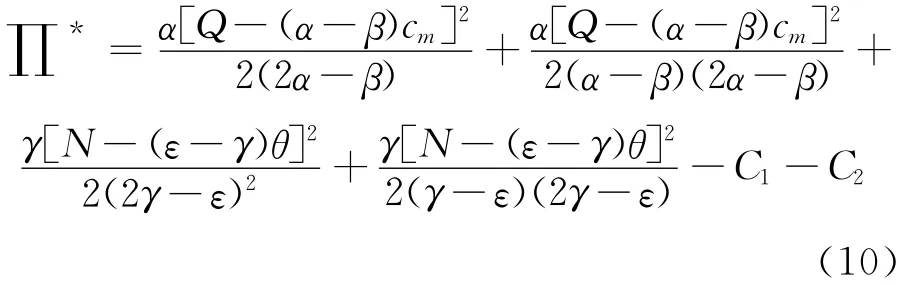
2．3 零售商集中决策

零售商集中决策时，闭环供应链模型如图3所示．除了零售商决策方式与2．2不同，其他假设均保持一致．这种博弈关系下，两个零售商首先决定他们的最优零售价格P和回收价格P0，并共同承担废旧产品回收的固定成本C，且令C＞，1C＞；根据Stackelberg博弈的假设，制造商将2由零售商的市场售价来决定其对零售商的批发价格W 和回收价格W0．此时产品的市场需求函数为D（P）＝Q－αP＋βP，废旧产品回收量为D0（P0）＝N＋γP0－εP0．

图3 零售商集中决策的闭环供应链系统

同2．2解法可得，零售商集中决策时零售商和制造商的收益分别为：

则两个零售商的收益均为：

此时，供应链的整体收益为：

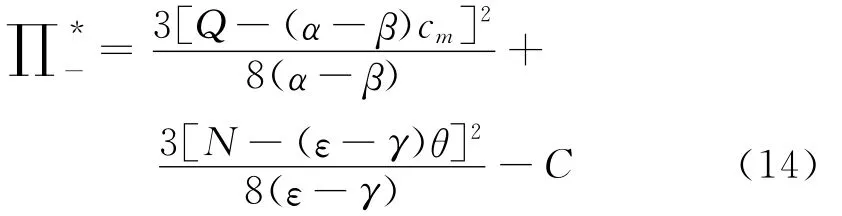
3 模型分析

最后比较这两种决策方式下供应链的整体收益：

即在两种决策方式下，供应链的整体收益存在差异．如果式（15）大于0，说明供应链的整体收益在零售商集中决策时较大；如果式（15）小于0，说明供应链的整体收益在零售商分散决策时较大．

4 数值算例

某电子产品在回收再利用过程中，由两个不同零售商负责，通过一个制造商再制造流通销售．根据式（7）～（10），（12）～（14）的模型要求，令α＝50，β＝2，ε＝10，γ＝1，cm＝30元，cr＝10元，N＝100，C1＝80元，C2＝70元，C＝40元（部分参数来源：文献［7］），得到不同市场容量Q下闭环供应链各成员及供应链整体的收益情况，见表1．

表1 不同市场容量Q下闭环供应链各成员及整体收益的计算结果 元

对表1中供应链上各成员和整体在零售商分散决策和集中决策情境下所得收益求差，并对差值作图．

令制造商在零售商分散决策和集中决策情境下的收益差为Δ∏M＝∏M分散－∏M集中，结果如图4所示．曲线在横轴上方，即为正值，故制造商在零售商分散决策情境下取得较大收益，且市场容量Q越大，制造商选择零售商分散决策的优势越明显．

图4 制造商在零售商分散决策与集中决策情境下的收益差

令零售商1在分散决策和集中决策下的收益差为Δ∏R＝∏R分散－∏R集中，同理，零售商1112的收益差为Δ∏R＝∏R分散－ ∏R集中，结222果如图5和图6所示．两条曲线均在横轴下方，故零售商在二者集中决策情境下取得较大收益，且市场容量Q越大，集中决策的优势越明显．

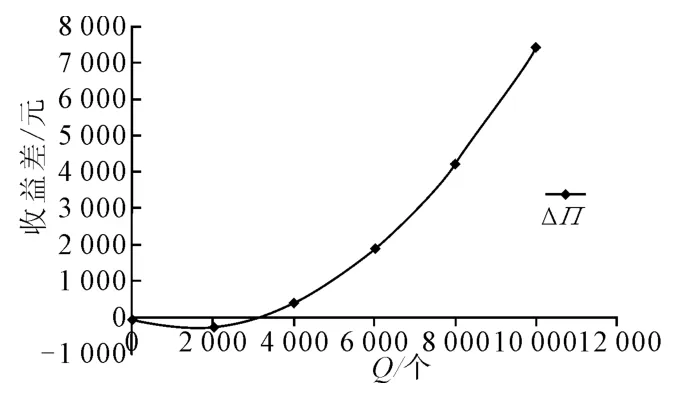
图5 零售商1在2种决策情境下的收益差

图6 零售商2在2种决策情境下的收益差

图7 零售商分散决策与集中决策情境下供应链整体收益差

曲线与横轴交点Q≈3 107处，此时两种决策情境下供应链整体收益相同．由图7，当Q＜3 107时，供应链的整体收益在零售商集中决策时较优；当Q＞3 107时，供应链的整体收益则在零售商分散决策时较优，且随着Q的增加，优势越明显．

5 结束语

本文构建了包含一个制造商和2个零售商的闭环供应链系统，零售商可以选择分散决策与集中决策2种决策方式．与以往研究不同的是，本文结合实际情况，对2个零售商回收废旧产品的价格进行了区分．研究发现，信息完全对称时，零售商决策方式不同，供应链中各节点收益情况和供应链整体收益也不同．制造商的收益在零售商分散决策时优于零售商集中决策时，零售商的收益则受益于零售商间的合作，并且闭环供应链的整体收益在市场容量较大时选择零售商分散决策获得的收益较高，而在市场容量较小时选择零售商集中决策获得的收益较高．

本文在进一步研究中，将同时考虑制造商从两个零售商处的回收价格也不相同的情境，进而探讨闭环供应链中各成员及供应链整体的收益分配的影响因素与收益波动规律．

［1］JAYARAMAN V，GUIDE V D R，Srivastava R．A closed－loop logistics model for remanufacturing［J］．Journal of the Operational Research Society，1999，50（5）：497－508．

［2］GINSBURG J．Manufacturing：once is not enough［J］．Business Week，2001（16）：128－129．

［3］SAVASKAN R C，BHATTACHARYA S，Van WASSENHOVE L N．Closed－loop supply chain models with product remanufacturing［J］．Management Science，2004，50（2）：239－252．

［4］FLEISCHMANN M，KRIKKE H R，DEKKER R，et al．A characterization of networks for product recovery［J］．Omega，2000，28：653－666．

［5］尤建新，隋明刚，杜 鹃．闭环供应链中可修理库存优化模型与算法［J］．同济大学学报：自然科学版，2004，32（11）：1534－1539．

［6］CATTANI K D，GILLAND W，SWANMINATHAN J M．Boiling frogs：pricing strategies for a manufacturer adding a direct channel that competes with traditional channel［J］．Production and Operation Management，2006，15（1）：40－56．

［7］郑 鑫，朱晓曦，马卫民．基于Shapley值法的三级闭环供应链收益分配模型［J］．运筹与管理，2011，20（4）：17－22．

［8］牟小俐，梅宝林．努力水平影响下三级闭环供应链收益分配问题探讨［J］．商业时代，2012（29）：40－41．

［9］易余胤．不同市场力量下的再制造闭环供应链决策研究［J］．商业经济与管理，2008，7（7）：24－30．

［10］刘伟华，季建华，张 涛．基于物流服务组合的两级物流服务供应链利润分配模型［J］．武汉理工大学学报：交通科学与工程版，2008，32（4）：589－592．

［11］SHAUHAN S S，PORTH J M．Analysis of a supply chain partnership with revenue sharing［J］．International Journal of Production Economics，2005，97（1）：44－51．

［12］张东堂，武 东，周永务，联盟博弈下基于shapley值法的三层供应链协调机制［J］．工程数学学报，2011，8（6）：763－769．

［13］马士华，王 鹏．基于Shapley值法的供应链合作伙伴间收益分配机制［J］．工业工程与管理，2006（4）：43－49．

［14］施国洪，朱孔华．基于价格与服务竞争的供应链收益分配模型的研究［J］．科技管理研究，2012（17）：225－228．

［15］刘家国，李 俊．基于零售商决策的供应链收益分配及风险弹性研究［J］．哈尔滨工程大学学报，2012，33（3）：398－402．

［16］吕培培，王炬香．两个在线零售商参与的供应链收益分配问题研究［J］．青岛大学学报：自然科学版，2012，25（2）：77－82．