基于LOG算子边缘检测提取特征点的平显振动算法研究
2014-01-16王涛
王涛
(中航工业洛阳电光设备研究所 河南 洛阳471009)
平显图像的抖动将直接影响飞行员的视觉效果。目前,评估平显成像系统质量一般都是通过人眼对振动情况下平显图像的长时间观察做出判断,主观因素较大,容易产生误判。因此,研究一套实时客观的平显图像振动检测系统具有重要意义。
1 运动估计算法的选取
运动估计是图像振动检测技术的核心,获得精确的图像序列帧间偏移向量的方法就是运动估计[1-2]。运动估计的准确性与实时性极大的影响着整个系统的性能。
前后相邻的两幅图像的映射关系是由前一帧图像和偏移量共同作用的函数,即

其中,Im g(i)表示前一帧图像,g(d x,d y)表示偏移量,Im g(i+1)表示后一帧图像。
运动估计算法在振动检测、电子稳像、视频压缩等领域广泛被使用[3]。关于运动估计的算法有很多,包括块匹配法、灰度投影法、特性匹配法等[4-5]。
通过对各种运动估计算法的研究与分析,比较它们的优缺点,得到表1。

表1 运动估计算法的比较Tab.1 Comparison of motion estimation algorithm
由表1可知,特征匹配的优越性高,而且对于其缺点可以采取一些算法补救,来提高匹配的精度。所以本文采用基于特征匹配的振动检测算法。
2 特征匹配算法的选取
2.1 基于特征点的振动检测算法分析
振动检测算法的重要思路之一就是“特征匹配”,它的实质就是构造出某种相关的运算机制,然后得到图像帧与帧间的运动向量。它主要依赖于图像的某个或某些特征,因此有比较高的精度。这里的特征包括点特征、线特征、面积特征等。点特征是应用范围最广的一种特征量,与直线特征相比较,点特征具有易提取、计算量小的优点。可以通过多个特征点来保证算法的稳定性和精确性。特征点匹配算法的原理是分别在参考帧图像和当前图像选取一些特征点,然后对特征点进行相关的匹配,最后求出运动向量。
本文是要满足实时振动检测的要求,即在实现振动检测的同时达到很好的实时性,选择基于特征点匹配,是因为它具有以下的特点:
1)精度高
本系统的目的就是检测出振动的幅度,检测出图像序列间的不规则运动,使观察者观察、分析起来更加方便,因此较高的精度是必不可少的。而特征点是个局部的特征,它的匹配对位置的变化相对比较敏感,当选取多个特征点进行匹配时,可大大提高匹配精度。
2)实时性好
实时性好的实质是帧处理率高,即每一帧图像的处理速度快,这样在检测系统中能够及时反映实际中的变化。图像的特征点的个数比图像的整个像素点的个数少很多,因此,可以大大提高匹配时的速度。
2.2 特征点提取算法的分析
一般常用的提取特征点的方法有:基于角点提取,如Susan法、Harris法等;基于兴趣点提取,如Moravec操作数、Forstner操作数等;基于边缘提取,如Log算子、Canny算子等。
2.2.1 基于角点提取算法
图像中的角点一般指图像边界上曲率高 (即曲率变化明显)的点。基于角点的算法有很多,如Susan法、Harris法、Kitchen法等。Harris算子[6]是1988年C.Harris和M.J.Stephens提出的基于信号强度的点特征提取算子。该算子引入了信号处理中自相关函数理论,将图像的局部自相关函数与角点检测紧密的结合在一起,最后是通过对特征值的分析判断待检测点是否为角点。该算子计算量相对小,因为它只用到灰度的一阶差分以及高斯滤波。由于用到图像的一阶导数,所以当图像存在旋转、灰度变化或视点变化时,不影响角点提取的效果,而且Harris算子的稳定性也比较高。利用Harris算子对平显图像进行特征点提取结果如图1所示。
2.2.2 基于兴趣点提取算法
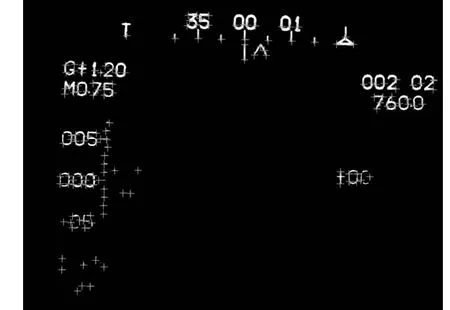
图1 Harris算子提取特征点图Fig.1 To extract the feature points by Harris
相对于领域表现出某种奇异性的点称为兴趣点,例如一些在局部区域中各个方向上灰度变化最大的像素点。它们容易提取,并且对信号的噪声、数据采集时参数变化和图像变换等具有很好的鲁棒性。一般常用的算法有Moravec算子、Forstner算子、Hannah算子等。
Moravec在1977年提取利用灰度方差提取特征的方法,随后这种方法被称为Moravec算子。该算法是沿着图像中的每一个像素点的4个方向,即水平、垂直、对角线和反对角线计算其灰度差,选取最小值作为响应值,最后通过局部非极大值抑制检测出特征点[7]。该算法思想简单,但是也造成它的局限性,即只利用4个方向计算,这样导致该算法在方向性上的缺陷。而且该算法对噪声的抑制性差,容易把一些孤立点和边缘点当做角点提取出来,准确率不高。基于此算子提取特征点情况如图2所示。

图2 Moravec算子提取特征点图Fig.2 To extract the feature points by Moravec
2.2.3 基于边缘检测提取特征点
一幅图像的边缘实质上意味一个区域的截止另一个区域的开始,它是以图像局部特征不连续性的形式出现,故边缘具体是指与其周围像素灰度有阶跃变化的像素点的集合。边缘检测是利用图像一阶导数的极值或二阶导数的过零点信息来提供判断边缘点的基本依据。因此,选取边缘点作为特征点,同样可以保证特征点定位的准确性和鲁棒性。
下面对比几种常见的边缘检测算子:
1)Roberts算子
由Roberts提出的一种算子,其原理是在2×2邻域上计算对角导数作为差分算子寻找边缘写成模板为:

由于Robert算子通常会在图像边缘附近的区域内产生较宽的响应,故采用上述算子检测的边缘图像常需做细化处理,而且边缘定位的精度不是很高。所以通过Robert算子图像处理后结果边缘不是很平滑。
2)Sobel算子
Sobel提出一种将方向差分运算与局部平均相结合的边缘检测方法。Sobel算子的原理是在3×3的邻域内做灰度加权和差分运算,利用像素点上下左右相邻点的灰度加权算法,依据在边缘点处达到极值这一现象进行边缘检测。
它采用的模板如下:

Sobel算子利用快速卷积函数使得它具有简单有效的特点,得到广泛的应用。但是,Sobel算子并没有严格地区分图像的背景和主体,即Sobel算子没有基于图像灰度进行处理,提取的图像轮廓有时并不能达到很好的效果。
3)LOG算子
Marr和Hildreth将高斯滤波和拉普拉斯边缘检测算法有机结合,提出了拉普拉斯边缘检测算子,形成了LOG(Laplacian of Gaussian)算法。之前叙述的算子都是利用边缘处的梯度最大来进行边缘检测,而拉普拉斯边缘检测是利用拐点处二阶导数为0,也就是寻找边缘可以通过寻找二阶导数的零交叉点来完成。以模板形式表示如下:

由于一阶导数对噪音敏感,二阶导数对噪音就更敏感,因而不稳定。所以LOG算法就是在用拉普拉斯算子之前,先用高斯滤波器对图像进行平滑。该算子具有以下特点:
①节省计算时间。其它的微分法,需要计算不同方向的微分,而LOG算法无方向性,不用计算不同方向的微分,因此可以缺省这部分计算量,从而节省计算时间;
②由于LOG算法先对图像进行平滑,这样尺度小于σ(高斯分布的均方差)的图像强度变化可以被消除;
③边缘连续性好、定位精度高,可以提取对比度较弱的边缘点。
综上所述,Robert算子通常会在图像边缘附近的区域内产生较宽的响应,由于边缘定位的精度不是很高,所以通过其对图像进行处理后结果边缘不是很平滑;Sobel算子并没有将图像的主体与背景严格地区分开来,它没有基于图像灰度进行处理,故提取的图像轮廓有时并不能令人满意;LOG算子在边缘检测中是让图像与高斯滤波器进行卷积,这样既对图像进行了平滑又降低了噪声,并且LOG算子定位精度高,边缘连续性好,也可以较好提取对比度较弱的边缘点。利用3种检测算子分别对平显图像进行边缘检测,结果如图3~5所示。

图3 Robert算子Fig.3 Robert

图4 Sobel算子Fig.4 Sobel

图5 LOG算子Fig.5 LOG
综上所述,本系统采取LOG算子对图像进行边缘检测。
在对图像进行边缘检测后,将图像分成互不重叠的r×s大小的区域,在覆盖的图像区域中选取灰度最大的点作为特征点。
3 基于边缘检测提取特征点的振动检测算法
由于基于角点提取和基于兴趣点提取都是对整幅图像来进行搜索计算,所以算法比较复杂,计算量大,耗时长,不利于系统的实时处理。而基于边缘检测提取特征点是在边缘点中进行选取,这样无形中提高了特征点提取速度。
另外,当选取LOG算子对图像进行边缘检测还能弥补平显图像预处理中利用中值滤波去噪的缺陷。由于中值滤波对高斯噪声无能为力,但是LOG算子的特点就是对图像进行高斯滤波然后再边缘检测,所以,当平显图像中包含高斯噪声,利用边缘检测也能达到去噪的效果。因此,本文选取基于边缘检测提取特征点。
但是基于边缘检测提取特征点算法在对图像进行边缘检测后,选取图像区域中灰度最大的点作为特征点,而根据本系统采集的平显图像(如图6所示)特征来看,灰度变化不明显,而且之前已经对图像进行二值化处理,整幅图像只有两种灰度值(0或255),显然利用灰度最大提取特征点已经不合理。因此,需对边缘检测提取特征点算法加以改进。

图6 原始图像Fig.6 Original image
3.1 边缘检测提取特征点算法改进
由于不能在已经进行阈值分割的图像中选取灰度值最大的点作为特征点进行提取,也就意味着不能从灰度变化这个方面对平显图像进行特征点提取。所以,需选取基于角点的原理提取特征点。具体方法是在对图像进行边缘检测处理后,利用基于角点提取特征点的方法对图像进行特征点提取,这样做不仅能克服不能直接利用边缘检测提取特征点,还能缩短基于角点提取特征点的时间,因为这里的角点都是在图像边缘上选取。具体计算过程如下:
1)LOG边缘检测。利用LOG算子进行边缘检测步骤:
①在一定范围内对图像做平滑滤波处理;
②利用差分算子检测在相应尺度上的图像边缘。使用的差分算子是各向同性的拉普拉斯二阶差分算子。常用5×5的LOG算子模板为:

图像与上述模板进行进行卷积后,提取边缘如图7所示。
2)角点提取。角点提取特征点的步骤:
①计算图像在边缘点上的梯度,也就是在水平X方向和垂直Y方向的差分Ix和Iy;
②构造一个与自相关函数相联系的矩阵C^,该矩阵的特征值λ1,λ2是自相关函数的一阶曲率,其公式为:


图7 LOG算子边缘检测Fig.7 Edge detection by LOG
其中Ix为x方向的差分,Iy为y方向的差分,I^表示为对I做高斯滤波,式(2)表示对操作的图像中的像素点,计算其在横向和纵向的差分,以及二者的乘积,这样得到的新的图像上的像素对应的值就是和IxIy,然后再对其进行高斯滤波。
③ 提取特征点:如果特征值 λ1,λ2是极大值,即两个一阶曲率值都高,那么该点就被认为是特征点。计算公式如下
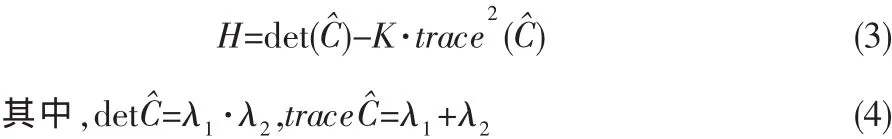
式(4)中 λ1,λ2为自相关矩阵C^的两个特征值。 det(C^)代表求矩阵行列式,trace(C^)代表求矩阵的迹,K是常数。其中k的经验取值范围为0.04至0.06。K·trace2(C^)是修正,目的是为了抑制边缘点的误检。
计算完后,将图像分成互不重叠的r×s个区域Ak,在Ak覆盖的图像区域中选取H最大的点作为特征点。选取结果如图8所示。

图8 改进算法后提取特征点图Fig.8 To extract the feature points by Improved algorithm
利用角点检测法对边缘进行特征点提取具有较高的鲁棒性和稳定性,能够在图像旋转、噪声干扰等情况下准确的检测特征点,具有较低的误检率。
4 结束语
本文首先对运动估计算法进行研究并对其进行比较,并研究了3种特征点提取算法,针对平显图像的特点,对基于边缘检测提取特征点算法进行改进,并在VC6.0环境下对其做了实验,分别计算了改进前和改进后提取特征点的时间,试验结果验证了改进算法的优越性。利用该算法提取图像序列的特征点后并进行特征点匹配,根据特征点对位移量计算图像序列的振动量,完成图像的振动检测。
[1]赵红颖,金宏,熊经武.电子稳像技术概述[J].光电精密工程,2001,9(4):353-358.ZHAO Hong-ying,JIN Hong,XIONG Jing-wu?.Overview of the electronic image stabilization technology[J].Optics and Precision Engineering,2001,9(4):353-358.
[2]周同.基于改进Canny边缘检测算子的电子稳像算法研究[D].苏州:苏州大学,2010.
[3]高晓明.电子稳像系统主要算法的研究 [D].西安:西安科技大学,2008.
[4]Pourreza H R,Rahmatt M,Behazin F.An electronic digital image stabilizer based on stationary wavelet transform(SWT)[J].ICIP 2003(2):383-386.
[5]Erturk S Dennis T J.Image sequence stabilization based on DFT filtering.IEEE Proc.On Image Vision and Signal Processing,2000(127):95-102.
[6]刘宇斌.一种分阶段的高精度亚像素特征点提取方法[J].南华大学学报:自然科学版,2006,20(2):54-57.LIU Yu-bin.A method of extracting highly accurateSubpixel Features by stages[J].Journal o fN anhuaUn iversity(Sc ience and Technology),2006.06,20(2):54-57.
[7]郭飞飞.基于特征点的图像配准方法及其应用 [D].重庆:重庆大学,2010.
