嵌入式横流风扇翼型CFD分析方法

王苏娅

（西安铁路职业技术学院 陕西 西安 710014）

近年来，一项能够大幅提高翼型升力，减小阻力的新概念流动控制技术在国外得到了广泛的研究。这项技术是在翼型中嵌入安装横流风扇（cross-flow fan，CFF），依靠横流风扇的主动吸气，使翼型上表面分离的气流重新附着在翼型表面，达到提高升力系数，防止失速的目的。

推进翼飞行器的发明填补了固定翼飞机和直升机之间的空白。与固定翼飞机和直升机相比，该飞行器具有许多显著地优点[1]：

1）噪声低；

2）失速迎角大；

3）短距起降；

4）良好的低速大载荷特性。

随着CFD分析方法的进步，特别是非稳态雷诺平均N-S方法的提出，使得横流风扇内部流场的模拟成为可能。国内外都加快了对该领域的研究。

国外关于横流风扇翼型的理论研究工作也是刚刚起步，Kummer和Dang建立了横流风扇翼型的CFD分析模型和计算方法，比较了不同构型的横流风扇翼型在不同迎角下的气动特性，通过对比风扇转与不转时翼型周围的流场变化，显示了横流风扇显著的流动控制作用。之后Dygert通过水洞实验测量了Kummer和Dang设计的横流风扇翼型在不同工作状态下的流场特性，实验结果和理论计算取得了较好的一致性[2]。

我国现阶段关于此项理论的研究正处于起步阶段，还有待于进一步进行这方面的研究和讨论。

1 CFD分析方法

1.1 理论建模

横流风扇叶轮内部的流动可以看作是二维粘性紊流流动，叶轮的旋转和表面的曲率效应所产生的离心力使叶轮内部的流动非常复杂[3]。此外，横流风扇叶轮有限片数的影响及叶片的空间扭曲、流道的扩散等都容易产生流动的分离及二次流。因此针对横流风扇的特点，采用基于雷诺平均的NS方程和标准的Κ-ε湍流模型，对横流风扇叶轮内部的二维紊流流动进行CFD分析。

将NS方程进行雷诺平均，再将其中的雷诺应力项计入湍流模型，从而建立一组湍流平均量的封闭方程组，作为叶轮内部流场CFD分析的基本方程组，用笛卡尔张量形式表示为[4]：

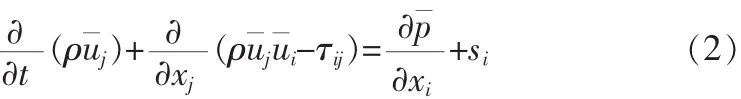
式中：t为时间；xi为笛卡尔坐标 （i=1，2，3）；u¯i为 xi方向流体的速度时均值；p¯为表压力的时均值；ρ为密度；sm为质量源项；si为动量源项；τij为质量张量项。

κ-ε湍流模型：

式中 Cε1、Cε2、Cε3、Cε4均为经验系数，分别为：Cε1=1.44，Cε2=1.92，Cε3=0.0 或 1.44（pB＞0），Cε4=-0.33。

1.2 几何建模

为了减小三维效应，一般都在扇翼飞行器机翼两端加挡板，因此对机翼的数值模拟可简化为对其翼型的数值模拟。本文计算的扇翼飞行器的翼型如图l所示。

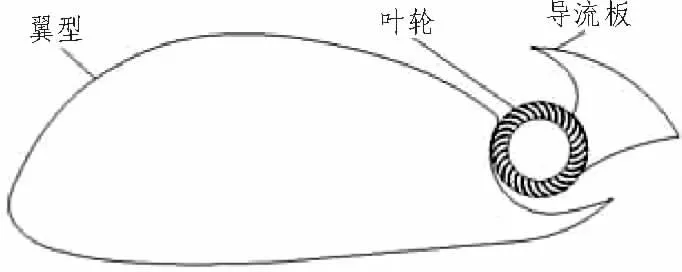
图1 嵌入式横流风扇翼型总体构型Fig.1 Embedded cross-flow fan airfoil overall conformation

为了充分发挥横流风扇的作用，需要保证足够的安装尺寸，所以横流风扇推进式飞行器一般采用厚翼型，翼身融合设计。厚翼型内部空间充裕，装载量大，如果不采用加装横流风扇的措施，即使在低迎角情况下，厚翼型的尾流区也会非常大，在很小的迎角下就会发生气流分离，这导致厚翼型对大多数飞行器来说并不适用。但是加装了嵌入式横流风扇以后，尾流被风扇吸入，气流重新附着在翼型表面，从而消除了气流分离，并产生了很高的升力系数。CFD仿真结果表明40°迎角时加装横流风扇的GOE570翼型在风扇转动时其升力系数可以达到6以上。这就大大减小了飞行器起飞速度，缩短了滑跑距离。

本文中分析所用的几何模型总体构造如图1所示，使用后缘截断的GOE570翼型，展长为1.38 m，弦长选为633 mm，风扇半径49.6 mm，30个叶片，出气口高度36 mm，叶片为双圆弧结构，最大厚度为1.5 mm。

图2所示为本文中翼型内部风扇腔体的构造形式以及导流板的运动情况，进气口高于翼型气动表面，通过抬高进气口可以消除翼型厚度对风扇尺寸的限制，风扇上缘高出翼型表面也可增强吸气效果，提高流动控制能力。后端导流片可上下偏转，保证尾流沿来流方向喷出，可有效减小尾流区域，并可提供矢量推力。对于气流的控制则通过导流板以及襟翼的运动来达到目的。

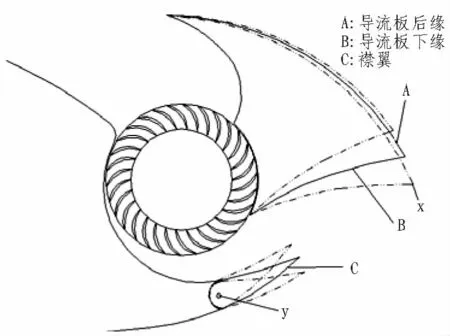
图2 横流风扇翼型内部腔体结构Fig.2 Cross-flow fan airfoil interior cavity structure

导流板后缘A与下缘B在x处铰连，襟翼C通过轴y连接在机翼上。襟翼通过舵机实现偏转运动，为了简化出气口的气流状态，C与导流板在两边挡板处用平行四边形结构连接，通过C的转动带动导流板的偏转。A采用可伸缩结构，当B转动时，A能够跟随运动。这样，在出气口高度不变的情况下，实现出气口角度的偏转，进而实现对飞行器飞行姿态的影响。

1.3 网格划分

为了获得准确的计算结果，应该保证有足够大的计算区域，这里采用边长为20C×15C的长方形计算区域，先在CATIA中绘制横流风扇翼型和外部的方形计算域，导入Gambit进行布尔运算后，以翼型弦线中点为圆心，长轴为1.7C，短轴为0.9C，确定一个椭圆，包围翼型，计算区域的分界线设为interior类型，不会影响计算结果。

最终的分析模型由236 017个网格单元组成，如图3和4所示，由于叶片尺寸较小，四边形边界层网格对叶片外形的影响较大，因此在绘制网格中全部采用三角形网格，在二者的计算结果中差别不大，因此采用三角形网格完全能够满足计算要求。

图3 叶片周围网格生成Fig.3 Blade weeks bounding mesh generation

该分析模型涉及叶轮的转动，需要建立多重坐标系进行计算，所以在叶片所在的环形区域的内侧和外侧各定义一个交接面，通过这两个交接面，将腔体内部划分为3个网格区

图4 翼型表面网格生成Fig.4 Airfoil surface mesh generation

域：叶片区域、外腔和内腔。其中叶轮区域设为转动的，逆时针转动为正，外腔和内腔相对于叶轮区域是静止的，叶轮区域的气流流动通过两个交接面传递给内外腔体内的气体，从而影响整个计算域内的气流流动。因为叶片区域流动最为复杂，为了准确描述流场，此处网格应该较为密集，内外腔体内的网格可以布置得较为稀疏，如图5所示。

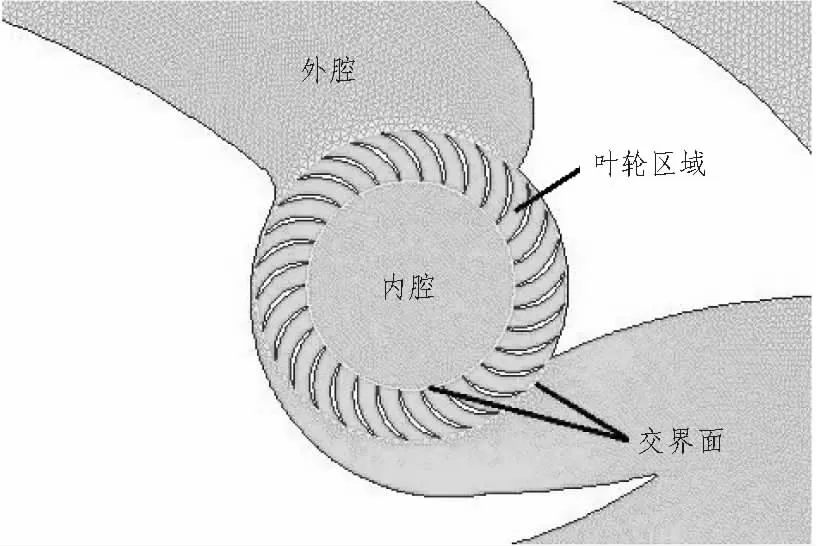
图5 叶轮周围网格生成Fig.5 Impeller weeks bounding mesh generation

翼型后端靠近风扇处流动非常复杂，既有紊乱的尾流，又有横流风扇的吸气作用，相比而言，翼型前端的流场要简单得多。所以在翼型表面布点时，前端稀疏后端紧密，如图6所示。椭圆内部气流流动受翼型影响较大，网格较密；椭圆外部流场受翼型影响较小，网格划分非常稀疏，如图7所示，这种设置可以提高计算速度，而不会对计算结果产生显著影响[5]。

图6 翼型周围网格生成Fig.6 Airfoil weeks bounding mesh generation

图7 整个计算区域网格生成Fig.7 The entire computational domain mesh generation

因为腔体内部构造较为复杂，采用结构化网格难度较大，所以该分析模型采用了自适应的非结构化网格，通过CFD仿真计算和实验结果的比较表明此种网格模型能够较好地模拟翼型表面以及横流风扇内部的气流流动，并且具有较高的计算准确度。

1.4 边界条件和初始条件设定

计算区域以左下方为速度入口，右上方为压力出口为边界条件，因为这里研究的是低速飞行，采用不可压流，而且需要考虑定常的水平来流，所以在入口处选用速度入口边界条件。这一边界条件用于定义流动速度和流动入口的流动属性相关的标量，适用于不可压流。出口边界设为压力出口，其静压值设为环境压强，因为该分析模型在出口处没有产生回流，所以不需要指定出口处的回流条件。

横流风扇翼型的流场分析属于非稳态问题，所有计算变量在开始计算以前都应该有一个初始值，这样才有可能根据时间步长计算场变量随时间的变化，在这里初始计算区域选为in。

1.5 选定计算模型

CFD计算采用二阶双精度求解方法，该模型适用于不可压流动，而且对精度有特殊要求，所以选择二阶隐式求解器。湍流模型采用标准κ-ξ两方程模型，κ-ξ模型是针对湍流发展非常充分的湍流流动来建立的，但是在近壁区内的流动，湍流发展并不充分，使用κ-ξ模型进行计算会出现问题，所以应该选择增强壁面措施加以解决。

因为涉及转动模型，所以采用非稳态解法，运动模型选为多重坐标系。湍流强度设为1%，湍流粘性比设为5，Joseph Kummer通过研究表明虽然入口湍流参数对于单独的翼型计算，尤其在准确预测翼型失速特性时非常重要，但在这里，因为嵌入式横流风扇的吸气效果和流动控制能力，湍流参数的选取对最终的计算结果影响并不大[6]。

1.6 时间步长和收敛准则

非稳态的模拟仿真需要选择合适的时间步长，以及每个时间步长的收敛标准。对于横流风扇流场仿真，一个时间步长设为叶片通过周期的1/20（例如，30个叶片的横流风扇一个转动周期内包含600个时间步长），这样的设置可以较好地记录非稳态流动并获得非常好的收敛解。

在一个时间步长内，迭代过程不断进行，直至升力系数及阻力系数等均达到收敛状态。因为计算区域为20C×15C，叶片转动时腔体内气流环境非常复杂，而且横流风扇吸入的是高度紊乱的翼型尾流，在来流和风扇吸气的综合作用下，翼型表面气流要达到稳定需要很长的计算时间。

1.7 计算模型的检验

为了检验本文建立的CFD分析模型是否正确，先计算40°迎角2 000 rpm时横流风扇翼型的气动特性，得出此时翼型周围流场的速度等值线如图8所示。Syracuse大学的Joseph Kummer率先做过横流风扇翼型的CFD分析，翼型弦长为4.572 m，风扇直径为0.64 m，40°迎角时来流速度设为15 m/s，风扇转速为1 250 rpm，计算得到的翼型周围流场的速度等值线如图9所示。和Kummer计算40°迎角风扇转动时的速度等值线图较为接近，但本文与Kummer的设计还有一定差距，由图8可以看出，在靠近进气口的翼型表面依然存在轻微的气流分离，而且翼型的尾流区域明显比Kummer的分析结果大，表现在气动特性上，就是本文得到的升力系数比Kummer算得的大了5.96%，而净推力大了13.4%，见表1。

图8 本文40°迎角风扇转动时的速度等值线Fig.8 The 40°Angle of Attack the Fan Rotation Speed Isoline

图9 40°迎角风扇转动时Kummer计算的速度等值线Fig.9 40°Angle of attack the fan rotates speed isoline of kummer calculation

表1 本文CFD分析结果和Kummer计算结果的比较Tab.1 CFD Analysis Results Comparison Between This Paper And Kummer

本文在CFD分析参数的设置上和Kummer的设置完全相同，考虑到具体设计参数的差异，以及网格划分方法的不同，两者计算结果的差距是很小的，所以本文建立的CFD分析模型能够正确模拟横流风扇翼型周围的流场特性。因为本文设计为小型飞行器，因此我们在此基础上缩小了该模型并分析了飞行器在不同飞行姿态下的气动特性，为将来的设计工作提供理论指导，可以显著缩短研制周期，降低研制成本。

2 结束语

本文主要进行了基于横流风扇技术的小型推进翼飞行器在不同控制参数下流动控制对飞行姿态影响的分析。该飞行器在机翼后缘安装嵌入式横流风扇，机翼上表面的气流被吸入腔体内，经加速后从后缘喷出产生推力[7]。本文采用计算流体力学方法，建立了推进翼飞行器机翼流场的二维计算模型，用多重坐标系法建立分析方法，并和相关实验结果取得了较好的一致性。

本文CFD计算部分使用商业计算流体力学软件Fluent完成通过Fluent软件分析了不同导流板角度以及横流风扇在不同转速下的气动特性并进行了相关计算，通过对计算结果的分析确定了这两个参数对飞行器飞行姿态的控制影响。

[1]Koo H M.Experimental study of the noise and the performance of cross-flow fans in room air-conditioning systems[J].Noise Control Engineering Journal，2000，48（2）：41-47.

[2]杨波，钟芳源，袁辉靖.横流风机内部流动试验研究机 [J].机械工程学报，2000，36（6）:68-70.YANG Bo，ZHONG Fang-yuan，YUAN Hui-jing.Crossflow experimental study of flow fan machine[J].Chinese Journal of Mechanical Engineering，2000，36（6）:68-70.

[3]陈次昌.横流式风机内部流动的研究[J].农业机械学报，1995，26（4）:90-94.CHEN Ci-chang.Study on the internal flow of cross-flow fan[J].The Chinese Society of Agricultural Machinery，1995，26（4）:90-94.

[4]赵京华，万淑敏.横流风机工作性能的试验研究[J].天津商学院学报，1995，15（4）:1-6.ZHAOJing-hua，WANShu-min.Experimental study on working performance of the cross-flow fan[J].Journal of Tianjin University of Commerce，1995，15（4）:1-6.

[5]Lazzaretto A，Toffolo A，Martegani A D.A systematic experimental approach to cross-flow fan design[J].Journal of Fluids Engineering TransactionsoftheASME，2003，125（4）：684-693.

[6]曾烘江，黄聪.机械设计从入门到精通进阶篇[M].北京：中国青年出版社，2004.

[7]韩占忠，王敬，兰小平.流体工程防真计算实例与应用[M].北京:北京理工大学出版社，2004.