一组高效LDPC码空间通信方案设计与实现
2014-01-16马明晓安军社
马明晓 , 安军社
(1.中国科学院 国家空间科学中心,北京 100190;2.中国科学院大学 北京 100190)
Gallager[1]于1962年首次提出基于稀疏校验矩阵的LDPC(低密度奇偶校验)码,但受限于当时的硬件实现水平和译码理论水平,并未得到足够的重视。20世纪90年代之后,编码界对置信传播算法展开广泛研究,LDPC码的重要性被重新发现。Mackey[2]于1999年证明在采用基于置信传播的迭代译码时,LDPC码的性能逼近香农极限,随后LDPC码迅速成为各种研究的热点。
已被应用于多个领域的LDPC码因其性能优异,为很多协议所采用,其中 CCSDS(空间数据系统咨询委员会)于2006年和2007年分别发表了文档号CCSDS 131.1-O-1的白皮书和文档号CCSDS131.1-O-2的橙皮书,二者的编码矩阵有所差别,但均为准循环码。在2011年8月CCSDS发表了文档号CCSDS 131.0-B-2的蓝皮书中,确定了一套分别适用于近地和深空通信的编码标准协议。这一系列协议都预示着LDPC码在未来的空间通信领域将扮演更为重要的角色。
文中主要结合CCSDS蓝皮书推荐的(8160,7136)码,从数学角度深入阐述基于欧氏几何的LDPC码的数学模型、建立过程及优异性能,提出了此类LDPC码的普适性构造方法。同时,结合航天任务中对资源、功耗、码速率的严格要求,提出适用于空间卫星通信的完备编码方案,并使用FPGA进行了实现。
1 基于欧氏几何的QC-LDPC码的构造
不同LDPC码的差异主要取决于其校验矩阵H。QCLDPC码可以由行列数相同的稀疏循环方阵阵列的零空间给出[3]。 若正整数 c 与 t满足 c≤t,对于如下 c×t的 GF(2)上 b×b循环方阵阵列:

其有如下两个结构特征:1)每个循环方阵Ai,j的重量相对于行列数b而言很小;2)Hqc中任意两行(或列)相同位置是 1的数目不大于 1, 称之为 “行列约束”(row-column constraint)[4]。特征1)决定了Hqc中的每个循环方阵都是稀疏矩阵,因此Hqc是稀疏矩阵。特征2)行列约束保证了Hqc任意一个子阵的4个角上不能同时为1。于是Hqc的零空间定义了长度n=tb的QC-LDPC码Cqc,其Tanner图不含有长度为4的环,围长至少为6[5]。
而对于定义在GF(2)上的m维欧氏几何空间EG(3,23),其共有(2ms-1)/(2s-1)个 1 维平行子空间集合,其中每个平行子空间集合由2(m-1)s条平行线构成。我们可以利用欧式空间上1维平行子空间集合构造QC-LDPC码的校验矩阵,进而构造出生成矩阵,建立QC-LDPC码。
1.1 校验矩阵H的建立
考虑定义在 GF(23)上的 3 维欧式空间 EG(3,23),该空间共含有512个点和4 672条线,每条线由8个点组成;其中,73条线通过空间原点,剩下的4 599条线不通过原点。
定义EG(3,23)上一条不经过原点的线L[6]的关联向量为vL=(v1,v2,…,v511),其中,vL中的每一个元素与中除原点以外的点一一对应。EG(3,23)上不通过原点的4 599条线的关联向量可以分为 9个循环族 Q1,Q2,Λ,Q9,其中每个族含有 511个关联向量。每个族内的关联向量可以由其中的任意一个关联向量循环移位得到。 对于每个族 Qi(1≤i≤9),以 Qi中的关联向量为行,可以得到一个 511×511的循环方阵 Z1,Z2,…,Z9。这样便产生了9个行重与列重均为8的511×511循环方阵。由于欧氏几何中的两条线要么平行要么相交于一点,故它们的关联向量中相同位置是1的数目不大于1。由于Z1,Z2,…,Z9中的各行与各列均为 EG(3,23)中线的关联向量,因此循环方阵 Z1,Z2,…,Z9满足成对行列约束,即两个不同的循环方Zi阵Zj与,按行排列与按列排列均满足行列约束。
对于 1≤i≤9,令fi为第 i个循环方阵Zi的第一列,将 fi分裂为 两个长度 相同的新 列 fi,1和 fi,2,且 fi,1和 fi,2平 分 了 fi的重量,将 fi,1和 fi,2循环下行移位 510次,分别可以得到两个新的 511×511 循环方阵 Ai,1和 Ai,2,每个行重与列重均为 4。 由此可得循环方阵阵列=[Ai,1,Ai,2],称之为 Zi的列分解[5]。 对于 1≤j≤2,令 qi,j为 Ai,j的 第一行 ,将 qi,j分 裂为 两 个长度相同的新行平分了q i,j的重量,将循环右行移位510次,分别可以得到两个新的511×511循环方阵,每个行重与列重均为2。由此得到的循环方阵阵列称为Ai,j的行分解[5]。 对于j=1,2,将Z*i中的循环方阵Ai,j替换为其行分解,得到一个由4个511×511的循环方阵组成的2×2阵列:

Ji称为 Zi的阵列分解[5,7],Ji中的所有循环方阵都是 Zi的子阵。循环方阵Z1,Z2,…,Z9的阵列分解形成了一组循环阵列J={J1,J2,…,J9}。 由于 Z1,Z2,…,Z9满足成对行列约束,它们的子阵也一定满足成对行列约束。因此,J中的各阵列也一定满足成对行列约束。基于J中的循环阵列可以构造(8176,7154)LDPC码。
(8 176,7154)码建立在 J 的前 8 个阵列 J1,J2,…,J8的基础之上。阵列


于是便形成了如下由511×511循环方阵构成的2×16阵列:

1.2 生成矩阵G的建立
考虑(1)中给出的校验矩阵 Hqc,具体形式已由上面式(5)得出。 设其秩为r=cb,令矩阵

其与Hqc有着相同的秩cb,假设 Hqc的前(t-c)b列对应于(t-c)b个信息位,则我们需要构造Cqc的生成矩阵具有如下结构:
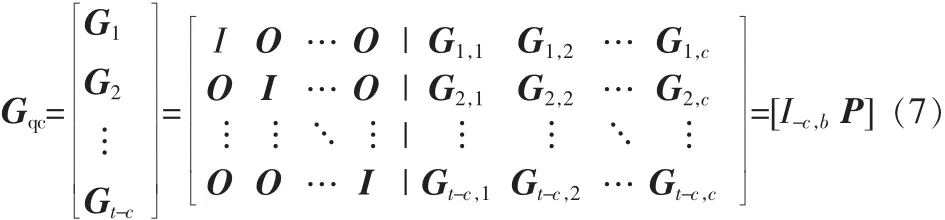
其中,I为b×b单位矩阵,O为b×b全零矩阵且对于 1≤i≤t-c 及 1≤j≤c,Gi,j为 b×b 循环方阵。 这种形式的生成矩阵Gqc称为系统循环形式(SCform),由左侧的单位矩阵It-c,b和右侧矩阵P构成。P为由b×b循环方阵组成的(t-c)×c阵列。这种结构允许使用简单的移位寄存器对QC-LDPC编码进行实现。
Gqc成为Cqc的生成矩阵的充分必要条件为[O],其中[O]为 cb×(t-c)b 的全零矩阵。 对于 1≤i≤t-c 及 1≤j≤c,令 gi,j为循 环 方 阵 Gi,j的 首 行 (或 首 列 ),一 旦 gi,j确 定 ,则 Gi,j可通过由 gi,j循环移 位的方式 得 到 , 故称 gi,j为 Gi,j的生 成 矢量。 于是,只要 Gqc中各个 Gi,j的首行(或首列)确定了,Gqc便能完全确定。
令各含有 b 个元素的向量 u=(1,0,…,0)O,=(0,0,…,0),对于 1≤i≤t-c,子阵 Gi的首行为

其中,u位于gi的第i个位置上。若Gqc为Cqc的生成矩阵则对于 1≤i≤t-c,必有=0。 令 zi=(gi,1,gi,2,…,gi,c),那么由=0 可得如下方程:

因为D为满秩的方阵,故D非奇异且有逆矩阵D-1,则由(9)式可得:

解(10)式,对于 1≤i≤t-c 可以得到 z1,z2,…,zt-c,由 z1,z2,…,zt-c进一步可以得到Gqc中个循环方阵的首行,进而Gqc可以被完全建立。
2 性能测试
对于由以上方法产生的(8 176,7 154)非规则QC-LDPC码[8],使用Matlab工具进行译码测试其误码性能,结果如下面两幅图所示。

图1 误比特率性能Fig.1 Bit-error-rate performance

图2 误分组率性能Fig.2 Frame-error-rate performance
以上结果均通过置信度传播算法进行80次迭代译码得出。从图1和图2可以看出,基于欧氏几何EG(3,23)构造的(8176,7154)码在编码增益、误码平台等方面有着优异表现。
3 QC-LDPC码的FPGA实现及航天应用方案
当今的飞行器和地面系统只能处理32-bit倍数结构的数据,显然(8176,7154)码并不满足这个条件。为了在实际的空间通信系统中获得应用,需将(8176,7154)码缩短和修整为(8160,7136)码并在编码时进行扰码、添加帧头[9]等操作,之后才能进入调制等之后的环节。
针对以上要求,本文设计了如图3所示的整合LDPC编码器,将数据分组、LDPC编码、扰码、添加帧头等操作整合到一个编码器中实现,极大地提高了FPGA资源的利用率,这一点在航天任务中尤为重要。
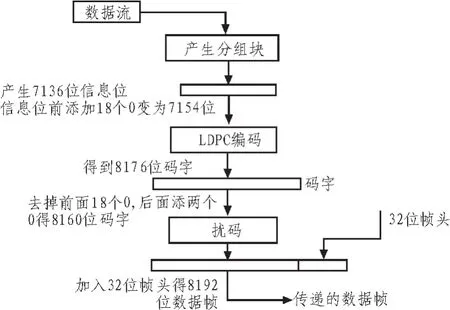
图3 编码器设计图Fig.3 The encoder design
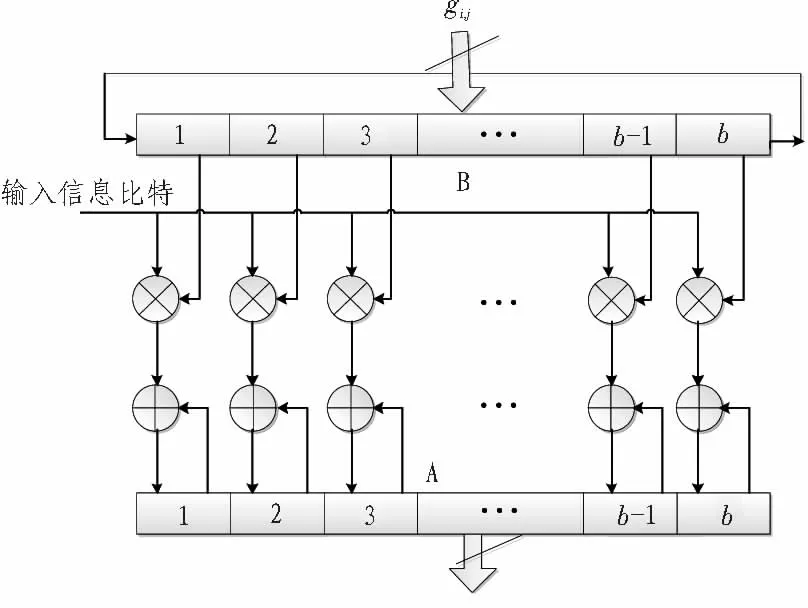
图4 移位寄存累加编码单元Fig.4 Shift-register-adder-accumulator
3.1 编码电路原理
根据Gqc中P矩阵的循环结构设计编码电路单元。设a=(a1,a2,…,a(t-c)b)为待编码的信息序列,将此序列分割为(t-c)个等长的序列 a=(a1,a2,…,at-c),其中,对 于1≤i≤t-c,ai=(a(i-1)b+1,a(i-1)b+2,…,aib)。 信息序列 a 所对应的码字为 v=aGqc且 v 为系统形式 v=(a,p1,p2,…,pc),其中对于 1≤j≤c,pj=(pj,1,pj,2,…,pj,b)为一段b位的校验位序列。对于1≤j≤c,由v=aGqc可知:


由(11)(12)可知,随着信息序列a逐位进入编码器,第j段校验位序列pj可以逐步的算出。对于1≤k≤t-c,在第k步, 累加和 sk,j=a1G1,j+a2G2,j+…+akGk产生并且存储于寄存器中。在第 k+1 步,部分和 ak+1Gk+1由(12)式算出并累加到 sk,j以形成下一个累加和 sk+1,j。 在(t-c)步结束后,由累加和 st-c,j便可得到第j段校验位pj。
基于上述编码过程,采用如图4所示的移位寄存累加电路单元(shift-register-adder-accumulator, SRAA)[4]。 此移位寄存累加编码单元中包括一个b比特的寄存器A,用于存储异或运算的结果;一个b比特的循环移位寄存器B,用于存储与生成循环子矩阵的行向量;b个两输入的与门和b个两输入的异或门。
3.2 串行编码方案
对于串行编码电路,其原理就是不断输入信息位,同时逐步计算校验位,信息位完全输入后,最终校验位便也得到。由此串行计算方式得到所有的校验位 p=(p1,p2,…,pc),共需c组SRAA电路,其原理图如图5所示。
对于由(8176,7154)码缩短所得的(8160,7136)码,采用Xilinx Virtex-4 FPGA进行调试,最高码速率可达210 Mbps以上,能够满足空间通信要求。

图5 串行编码电路Fig.5 Serial-encoding circuit
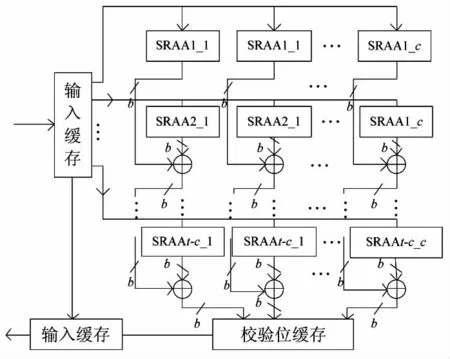
图6 并行编码电路Fig.6 Parallel-encoding circuit
3.3 并行编码方案
为满足图像传输等高速数据通信场合,还可用SRAA电路构建并行编码器。其基本思想是同时用(t-c)个SRAA电路完成式(17)中(t-c)个被加项的计算,如此只需b个时钟周期就能得到pj。用c组这样的并行SRAA电路,便能同时计算所有校验位,并行编码器结构图如图6所示。
并行计算会用到(t-c)个不同位置上的输入信息,因此需一组信息元完全输入后方能开始编码。另外,还需要一个码字的延迟时间方能得到连续平稳的输出码流,因此并行编码器的输出延迟为两个码字。经硬件测试知并行编码器最高输出码速率可达2 Gbps左右。与串行编码器相比,其速率的提高与所耗费的硬件资源是成比例的。为在速度与硬件资源之间取得折中,还可以设计并行路数为1与(t-c)之间的部分并行编码电路。
4 结束语
文中对一类基于欧氏几何的QC-LDPC码的数学基础及性能进行了分析,提出了该类码的普适性构造方法。并结合CCSDS 所推荐的(8 176,7 154)码和(8 160,7 136)码,对此类QC-LDPC码的硬件实现展开研究,采用SRAA电路单元分别设计了串、并行编码方案,并使用FPGA进行了实现,达到了很高的码速率,具有相当高的应用价值,适用于资源、功耗、码速率要求严格的空间通信系统。
[1]Gallager R G.Low density parity check codes[J].IRE Transactions on Information Theory,1962,8(1):21-28
[2]Mackay D J C.Good Error-Correcting Codes Based on Very Sparce Matrice[J].IEEE Transactions on Information Theory,1999,45(2):399-431.
[3]J.Xu, L.Chen,L.-Q.Zeng, L.Lan, S.Lin.Construction of low density parity-check codes by superposition [J].IEEE Transactions on Communications, 2005,53(2):243-251
[4]Li Z, Chen L, Zeng L, S.Lin.Efficient Encoding of Quasi-Cyclic Low-Density Parity-Check Codes[J].IEEE Transactions on Communications,2006,54(1):71-81.
[5]Yu K,Lin S,Fossorier M.Low density parity check codes based on finite geometries:A discovery and new results[J].IEEE Transactions on Information Theory,2001,47 (11):2711-2736.
[6]Lin S,Daniel J.Costello J.Error Control Coding:Fundamentals and Applications, 2nd ed.[M].Upper Saddle River, NJ:Prentice-Hall,2004.
[7]L.Chen,J.Xu,S.Lin.Near Shannon Limit Quasi-Cyclic Low-Density Parity-Check Codes [J].IEEE Transactions on Communications,2004,52(7):1038-1042.
[8]CCSDS 131.1-O-2.Low density parity check codes for use in near-earth and deep space applications[S].Washington D.C.,2007.
[9]CCSDS 131.0-B-2.TM synchronization and channel coding[S].Washington D.C.,2011.
