基于归一化方法的协同过滤推荐算法

陈小辉,高 燕,刘汉烨

（榆林学院 信息工程学院，陕西 榆林 719000）

随着计算机网络技术迅速发展，越来越多的人类活动依赖于互联网，人们可以通过网络购买各类商品，获取生活资讯，寻求合作和协助等等，但是面对海量的互联网信息，普通用户越来越难以及时获取有效的信息，在这种情况下能够提供高效的个性化的信息推荐显得尤为重要[1]。协同过滤推荐算法是目前应用最成功的推荐算法之一，在许多领域得到了广泛的推广。

协同过滤（Collaborative Filtering，CF)是根据用户的兴趣爱好、历史数据寻找与用户在这些方面有一定相似性的邻居，并且根据邻居的一些行为或评价数据对用户进行推荐。与基于内容的推荐系统不同，协同过滤推荐算法仅仅是依据用户对项目的评价寻找评价相似的若干邻居，而忽略数据详细内容，一般也不提取项目的文本特征向量，因为一般情况下如果不同用户对一些项目给出的评价相近，那么这些用户对其他项目的评价也会相似[2]。协同过滤推荐算法一般分为两类：基于内存的协同过滤(Memory-based CF)和基于模型的协同过滤(Model-based CF)。基于内存的协同过滤算法是目前应用最广泛的推荐方法，又可以进一步分为基于用户的协同过滤推荐和基于项目（item）的协同过滤推荐以及综合考虑用户和项目的推荐技术。基于用户推荐算法是依据邻居用户对某个项目的评分来预测当前用户对该项目的评分，基于项目的推荐算法则根据邻居项目的评分值来预测当前项目的评分[3]。

对于协同过滤推荐算法来说，核心是计算用户或项目之间的相似度，而在传统的相似度计算过程中，往往不能妥善处理用户评分向量（或项目评分向量）之间的向量空间长度差异，而且往往忽略邻居用户共有的评分项目（或多个用户对邻居项目的评分）的数值差异或者是严重弱化数值差异，为了解决这一问题，笔者提出了一种基于归一化方法的协同过滤推荐算法(NDCF)，该方法在计算相似度之前首先将用户对每一项目的评分值归一化到一个统一的值域范围，然后采用基于用户的协同过滤推荐算法对归一化后的不同向量空间中的用户向量进行相似性度量形成最近邻居，并产生归一化的项目评分预测，最后再根据当前用户在其他项目上的评分完成项目最终的评分预测，并进行推荐。

1 传统的协同过滤推荐原理

协同过滤推荐方法中最流行应用最为广泛的是基于内存的推荐算法，其实现原理最为直观。以经典的基于用户(User-based)的协同过滤推荐算法为例，它的基本思路是通过寻找与当前用户相似度最高的k个邻居，然后依据邻居对某个项目的评分来预测当前用户对该项目的评分[4]。这种推荐算法可分为3个实现步骤：数据定义、用户相似度计算和项目评分预测与推荐。

1.1 数据定义

数据定义实际就是定义用户评分矩阵R，R是一个n*m的矩阵，n和m分别代表矩阵中的用户数和项目数。矩阵中的元素值代表用户对项目的评价值，包括显式评分和隐式评分两种，显式评分一般指用户直接对项目的评价值，隐式评分则是根据用户的浏览行为如浏览频率、时间、购买等间接推测出的数值[5]。矩阵的用户向量（水平向量）代表特定用户对项目的评价值，项目向量（垂直向量）代表某个具体项目得到的用户的评价值。如果存在用户ux对项目iy的评分rxy，则评分矩阵R中有R[x,y] = rxy，用户评分矩阵R如式(1)所示。

1.2 相似度计算

协同过滤推荐本质是基于近邻的搜索方法，其实现核心是对用户或项目间的相似性的度量。常用的计算相似性方法主要有向量空间相似性度量方法（VSS）和皮尔森相似性度量方法（PCC）两种。向量空间相似性度量方法是把用户对项目的评分看作是一个n维向量，用户间的相似性是通过计算两个用户向量之间的余弦夹角来决定[6]。用户u和v之间的相似度SIM(u, v)计算如式（2）所示，式中Iuv表示用户u和用户v共同评分的项目集合。

皮尔森相似性度量方法是用来衡量变量的线性关系，是在向量空间相似性度量方法的基础上考虑了用户评分的数值差异，使用用户评分的偏差作为评分值参与计算，用户u和v的相似度SIM(u, v)计算如式（3）所示，其中代表用户u和用户v对各自已评分项目的平均评分，Iuv代表用户u与用户v共同评分项目的集合。

1.3 项目评分预测与推荐

使用式(2)或式(3)计算得到任意两两用户之间的相似值以后，对于特定的目标用户，可以得到与其相似度最大的N个邻居用户，需要进行预测的目标用户的某一未评分项目，可以按照一定的计算方法根据这些邻居对该项目的评分来得到，为提高预测准确度需要考虑到不同用户的评分尺度的不同，计算时候需要考虑用户对所有项目的平均评分，可利用公式(4)进行评分的预测，式中 表示用户u对项目i的评分用户u和用户v对各自已评分项目的平均评分，N(u)代表目标用户u的邻居用户集。在计算得到当前用户对于未评分项目的预测评分后，可以根据评分值对这些未评分项目排序，然后选择评分最高的若干项目进行推荐。

2 基于归一化方法的协同过滤推荐

2.1 传统协同过滤推荐算法的不足

传统的基于内存的协同过滤推荐因为其算法简单实用在较多领域得到了应用，但是仍然存在较多问题。特别是在相似度计算过程中，VSS算法和PCC算法都是基于用户对项目评价的数值进行直接统计去计算相似度，而没有考虑用户向量的差异与评分的数值大小[7]。例如图1，对于一个简单的用户评价矩阵，它包含5个用户和5个评分项目，用户对每一个项目的评分值在1和6之间。

图1 用户项目评分矩阵Fig.1 Scoring matrix of users and items

如果要预测用户u2对于项目i5的评分，采用VSS和PCC相似度算法可以得到Sim(u1，u2)的值为0.954 8和0.660 3，得到Sim(u2，u3)的值为 0.865 3 和 0.492 6，显然 Sim(u1，u2)＞Sim(u2，u3)根据这个计算结果，u1与u2的相似度比u2与u3的相似度大。而从图1可以看出u1的评分区间是[1,6]，而u2和u3的评分区间是[1,4]，所以u1与u2的相似度应当比u2与u3的相似度小，在计算u2对i5的评分时候应当参照的邻居是u3对i5的评分而不是u1。这个矛盾是因为皮尔森算法不能对处于不同向量空间的用户向量的评分风格差异进行有效处理，而向量空间算法则只关注用户向量之间的空间夹角，会忽略用户向量间的长度差异因此有必要寻找更合理有效的，符合实际情况的相似度计算方法从而改善推荐性能。

2.2 基于归一化方法的相似性度量方法

为了克服传统协同过滤推荐算法的不足，笔者尝试在传统算法中引入归一化数据处理过程。在形成用户评分矩阵以后，首先将所有用户的项目评分值归一到统一的值域空间，该处理过程假设任一用户向量对所有项目的评分不能全部相等。在实现过程中，对于评分矩阵R的每个行向量，使用该用户的最高评分值和最低评分值来归一化每一个项目评分，最后项目评分值位于区间[0,1]，归一化处理后用户u对项目i的评分 r'ui计算方法见式(5)。

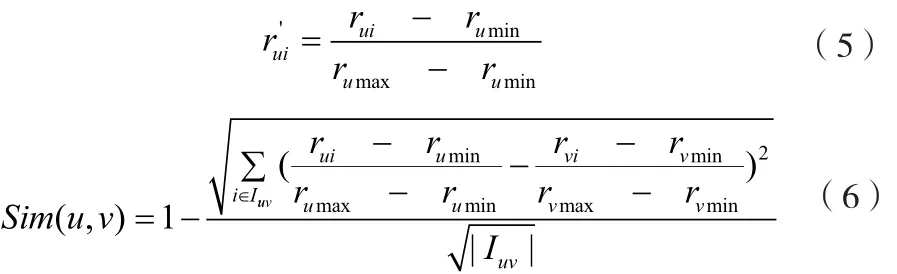
根据式（6）计算得到的Sim(u,v)∈[0,1]，值越大则用户u和用户v越相似，当等于0时表示两个用户完全不同，取1时表示两个用户相同。对于图1中用户评分矩阵数据计算可得Sim(u1，u2)和Sim(u2，u3)的值分别为0.791 5和0.855 7，则该相似性结果与事实相符。特殊情况当某个用户对所有项目的评分都完全一样的时候，会出现零除数的情况，但是由于所有的项目会涉及到推荐系统的各种商品、服务，有效用户的评分不会全部相同，所以可以忽略该情况。

为度量被评分的项目之间的相似性，可通过对原始评分矩阵R的每个项目的所有评分值（每一列）进行归一化处理，同样归一处理后矩阵中每列的值都在区间[0，1]上，式（7）给出了度量项目i和j之间相似度Sim(i,j)的计算方法，式中Uij表示对项目i和项目j都做出了评价的用户集合，|Uij|表示集合中用户的个数，rimin和rimax表示用户对项目i的最小和最大评分值，rjmin和rjmax表示用户对项目j的最小和最大评分值。

特殊情况当所有用户对某个项目的评分都完全一样的时候，会出现零除数的情况，但是由于对单个项目的评分会涉及到推荐系统的各类用户，评分在现实情况下不会全部相同，所以可以忽略该情况。

2.3 基于归一化方法的项目评分预测和推荐

基于2.2节提出的相似性度量算法，本节给出一种新的基于内存的协同过滤方法,当需要预测用户u对项目i的未知评分值时，该方法会根据用户的原始评分尺度来进行预测。在基于用户的项目评分值预测中用户u对项目i的预测评分可以通过式（8）计算，式中U表示与用户u相似度最高的同时对项目i进行了评分的k个用户的集合。

3 实验与分析

3.1 实验数据集

为了验证算法的有效性，采用Group Lens研究小组提供的Movielens 电影评分公开数据集（http://www.grouplens.org）对算法进行验证和评估。该数据集采集于一个电影推荐网站，包含了943位用户对1 682部电影的100 000个评分，用户评分矩阵的稀疏度为93.7%。实验中从原始评分矩阵中随机修改一部分评分项目，形成了10个数据密度分别为2%，4%，6%，8%，10%，12%，14%，16%，18%和20%的稀疏矩阵，使用稀疏度较高（数据密度较低）的原因是实际中的评分矩阵通常非常稀疏。

3.2 评价标准

为了检验项目评分的预测准确度，使用被广泛采用平均绝对误差（Mean Absolute Error，MAE)来衡量预测的有效性。MAE是预测值与真实值之间的绝对偏差的平均值，式（10）给出了MAE的计算方法，式中rui是指用户u对项目i的实际是指预测得到的用户u对项目i的评分值，N是被预测值的数量，MAE值越低，则说明预测的准确度越高。

3.3 实验方案

为了比对归一化处理协同过滤算法的有效性，采用了5种传统协同过滤方法与基于用户的归一化协同过滤推荐算法（NDCF）进行了对比实验：基于用户的平均数法（UMEAN)，该方法在计算未知项目的评分时，使用用户对所有项目的评分均值表示；基于项目的平均数法(IMEAN)，该方法在计算未知用户评分时，使用所有对当前项目评分用户的评分均值；使用PCC的基于用户的协同过滤（UPCC）；使用PCC的基于项目的协同过滤（IPCC）；混合使用UPCC和IPCC实现的一种协同过滤方法（WSRec）。实验采用五折交叉验证方法，对于10个稀疏矩阵中的每个评分矩阵，将用户评分记录按照4 : 1的比例划分为训练集和测试集，而且分别进行了5次划分，分别依据训练集中数据来预测计算测试集中数据并计算相应MAE值，最后统计得出5次实验的平均MAE值。实验中邻居规模数k分别取10,20,30,40和50，图2～图3给出了邻居规模为10和50情况下的实验结果。

图2 邻居数为10时性能比对图Fig.2 Performance comparison chart of 10 neighbors

图3 邻居数为50时性能比对Fig.3 Performance comparison chart of 50 neighbors

从实验结果比对中可以看出，基于归一化方法的协同过滤推荐（NDCF）的MAE值明显优于其他传统推荐算法，但是随着用户评分矩阵密度的增长NRCF相对于其他方法的MAE值变化不大，分析原因是优于评分矩阵越稀疏，用户向量的维度就越趋于多样，这导致NDCF在地密度评分矩阵上相比于其他方法拥有越好的性能。由于现实环境下的协同推荐系统中有效的用户评分矩阵一般都会非常稀疏。同时我们也观察到和其他推荐算法一样，随着邻居规模K值的增加MAE值在下降。图4描述了取评分矩阵密度density=0.1，邻居规模K从10增大到50对NDCF算法MAE值的影响，说明邻居数越多NDCF的预测精度越好，但是当K值增到到40到50之间时，MAE曲线已经趋于平缓，如果K值进一步增大会逐渐使噪声邻居增加，影响预测的准确性。总体来看相对于其他推荐方法，基于归一化方法的协同过滤推荐方法能够适应更宽泛的数据稀疏度，评分预测的性能也明显提高。

4 结束语

针对传统的协同过滤推荐算法的不足，本文提出了一种基于归一化方法的协同过滤推荐算法（NDCF），用于解决个性化的项目评分的预测和推荐问题。所提出的NDCF方法中包含了一种新的用户（项目）相似度计算方法，能够更加准确地找到相似的邻居用户或邻居项目，进而提高预测及推荐的性能。实验结果显示与传统推荐算法相比，NDCF方法能够明显提高评分预测的性能。

图4 邻居数对MAE值的影响Fig.4 Influence of neighbor number on MAE value

[1] 李聪，梁昌勇，马丽．基于领域最近邻的协同过滤推荐算法[J]．计算机研究与发展，2008,45(9): 1532-1538.LI Cong, LIANG Chang-yong , MA Li. A collaborative filtering recommendation algorithm based on domain nearest neighbor[J]. Journal of Computer Research and Development,2008,45(9): 1532-1538.

[2] 张光卫，康建初，李鹤松．面向场景的协同过滤推荐算法[J].系统仿真学报, 2006，18(22)：595-601.ZHANG Guang-wei, KANG Jian-chu, LI He-song. context based collaborative filtering recommendation algorithm [J].Journal of System Simulation, 2006，18(22)：595-601.

[3] Sun H, Zheng Z，Chen J, et al. NE.CF: A Novel collaborative collaborative filtering method for service recommendatioii[C]//2011 IEEE International Conference on Web Services (ICWS), 2011:702-703.

[4] ZHAO Zhi-Dan , SHANG Ming-Sheng . user-based collaborativefiltering recommendation algorithms on Hadoop[J]. Third International Conference on Knowledge Discovery and Data Mining, 2010:478-481.

[5] Salakhutdinov R, Mnih A, Hinton G. Restricted Boltzmann machines for collaborative filtering[C]// Proceedings of the 24th international conference on Machine learning, 2007: 791-798.

[6]Banerjee S, Ramanathan K. Collaborative filtering on skewed datasets[C]//Proceedings of the 17th international conference on World Wide Web, 2008:1135-1136.

[7] Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model[C]//Proceeding of the 14th ACM SIGKDD international conference on Knowledge discovery and Data Mining, 2008: 426-434.

[8] Sun H, Peng Y, Chen J, et al. A new similarity measure based on adjusted euclidean distance for memory-based collaborative filtering[J]. Journal of Software, 2011, 6(6): 993-1000.