3种大坝安全监控智能模型的比较
2014-01-16杨晓晓
王 泉,杨晓晓,王 超,刘 彪
(1.河海大学水利水电学院,江苏南京,210098;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京,210098;3.河海大学水资源高效利用与工程安全国家工程研究中心,江苏南京,210098)
0 引言
水利工程中,建立合理的大坝安全监控模型可实时在线监测大坝的安全状态,防患于未然,同时可以指导施工、反馈设计[1]。大坝安全监测项目主要包括应力、变形、裂缝、渗流等[2]。目前,大坝安全监测资料分析主要有回归统计法、神经网络理论、时间序列法、灰色理论、模糊数学、确定性模型和混合模型。传统的统计回归法需考虑因子的多重共线性,使用不便,有时效果欠佳;确定性模型和混合模型在大坝运行多年后无法准确考虑坝体和坝基的弹性模量;而神经网络以其智能化、可视化、网络化、易于实现等特征发展较快。未来,随着计算机技术的迅猛发展,神经网络具有强大的发展前景和生命力。目前,苏怀智[3]和宋志宇[4]对大坝安全监测的智能方法做了系统性研究;吕蓓蓓[5]、周洪波[6]和张飞[7]将神经网络模型用于大坝变形分析;张伟等[8]、谈小龙[9]和蒋国芸等[10]将支持向量机模型用于大坝安全监测中;潘华贤[11]、胡义涵[12]对极限学习机做了研究和应用,但目前极限学习机方法还未应用于大坝安全监控中。基于某混凝土坝实测资料,以极限学习机(ELM)为重点建立大坝安全监控模型,并详细分析、比较了它与BP神经网络和支持向量机回归(SVR)模型的运行性能差异。
1 基本原理
近几年,由于计算机技术和智能的迅猛发展,智能算法也发展较快。基于Matlab[13-15]平台工具,智能算法在大坝安全监控模型中能得到很好的应用。编制智能模型学习算法[16]的主要思路步骤为:产生训练集、创建训练模型、仿真测试、性能评价、预测。笔者着重介绍ELM的基本原理。
1.1 BP神经网络
BP神经网络由Rumelhard和McClelland于1986年提出,从结构上讲,它是一种典型的多层前向型神经网络,具有一个输入层、数个隐含层和一个输出层。层与层之间采用全连接的方式,同一层的神经元之间不存在相互连接。隐含层中的神经元多采用S型传递函数,输出层的神经元多采用线性传递函数。传统的BP神经网络采用误差反向传播算法作为有导师指导的学习算法,其指导思想是权值和阈值的调整要沿着误差函数下降最快的方向——负梯度方向。
1.2 SVR算法
支持向量机(Support Vector Machine,简称SVM)利用非线性变换将原始变量映射到高维特征空间,在高维特征空间中构造线性分类函数,能保证模型具有良好的泛化能力,又解决了“维数灾难”问题。SVM算法将转化为一个二次规划问题,从理论上讲可以获得全局最优解,从而解决了传统神经网络无法避免的局部最优问题。将SVM应用于回归拟合问题,得到回归型支持向量机(Support Vector Machine for Regression,简称SVR),取得了很好的性能和效果。
1.3 ELM
极限学习机(Extreme Learning Machine,简称ELM)是专门针对单隐含层前馈神经网络的新算法,改善了传统学习算法(如BP算法)固有的缺点:梯度下降算法需多次迭代而训练速度慢;容易陷入局部极小点;学习率η的选择敏感等问题。
典型的单隐含层前馈神经网络结构由输入层、隐含层、输出层组成,输入层与隐含层、隐含层与输出层神经元间全连接。其中,输入层有n个神经元,输出层有m个神经元。设输入层与输出层间的连接权值ω,隐含层与输出层间的连接权值β,隐含层神经元的阈值b,见公式(1)。
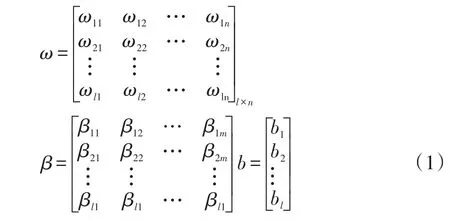
设具有Q个样本的训练集输入矩阵X和输出矩阵Y分别为
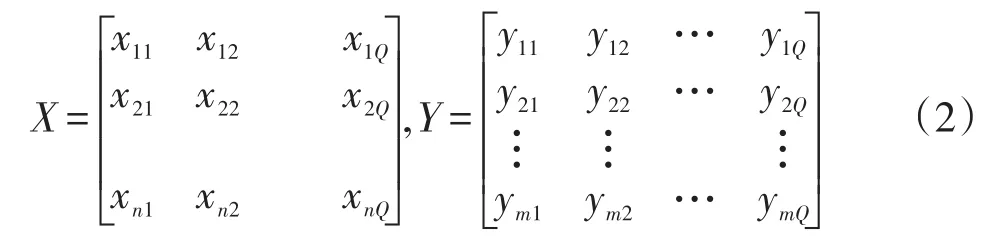
设隐含层神经元的激活函数为g(x),则网络的输出为
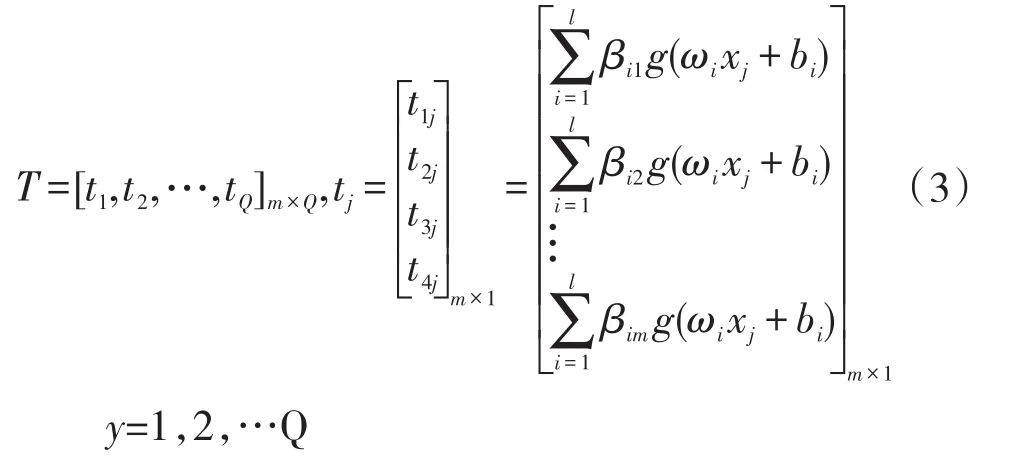
其中,ωi=[ωi1,ωi2,…,ωin],xj=[x1j,x2j,…xnj]T
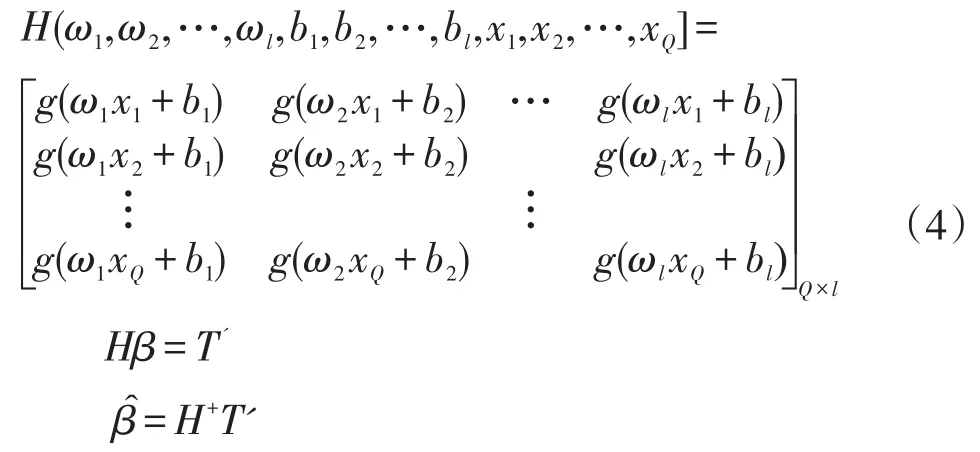
其中:T'为矩阵Τ的转置;H为神经网络的隐含层输出矩阵;H+为H的Moore-Penrose广义逆。
2 大坝安全监控模型
2.1 工程概况
某混凝土重力拱坝最大坝高76.3 m,坝顶宽8 m,最大底宽53.2 m,分为28个坝块,坝顶弧长419 m。在施工及运行过程中,坝体混凝土陆续出现了大量裂缝。大坝下游面105 m高程附近水平裂缝长300余m,横贯24个坝块,其中河床坝块的裂缝深度超过5 m;下游面115.5 m高程附近水平裂缝贯穿了16个坝段,经检测裂缝深度约为12 m;105 m检查廊道顶部和坝顶分布有纵向铅直裂缝,已经开展了工程修复。但未来裂缝监控仍是大坝安全监测重点。以该大坝实测裂缝开度资料为例,分别建立大坝裂缝开合度的BP神经网络、SVR和ELM模型。
2.2 样本输入量
实际工程中,大坝运行条件复杂,坝体的裂缝开合度受温度、水位、降雨、时效、施工、混凝土性能等多种因素的影响。根据现有的裂缝开合度模型[17],主要考虑温度、水位、时效因子。
水位因子:温度因子:

时效因子:
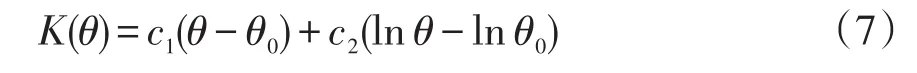
其中,H为监测日对应的上游水头,即上游水位与坝底高程之差;t为监测日到始测日的累计天数;θ为从始测日算起,每增加1天,θ增加0.01。
综上得,样本输入量为水位H、H2、H3、温度、时效θ、lnθ。
2.3 智能模型分析
实际建模时,选择2011~2012年监测序列作为样本,总共有729组数据,前680组为训练数据,能够完整反映裂缝开度的变化趋势,后49组为预测数据。
(1)实际训练BP神经网络时,隐含层的神经元个数对BP神经网络的性能影响较大。若隐含层神经元个数较少,则网络不能充分描述输入和输出变量之间的关系;若隐含层神经元个数较多,则会导致网络的学习时间变长,甚至会出现过拟合问题。在经验公式的基础上,确定隐含层神经元个数为10,其他采用默认参数。BP模型训练集拟合结果如图1所示,BP模型训练集拟合效果较好。
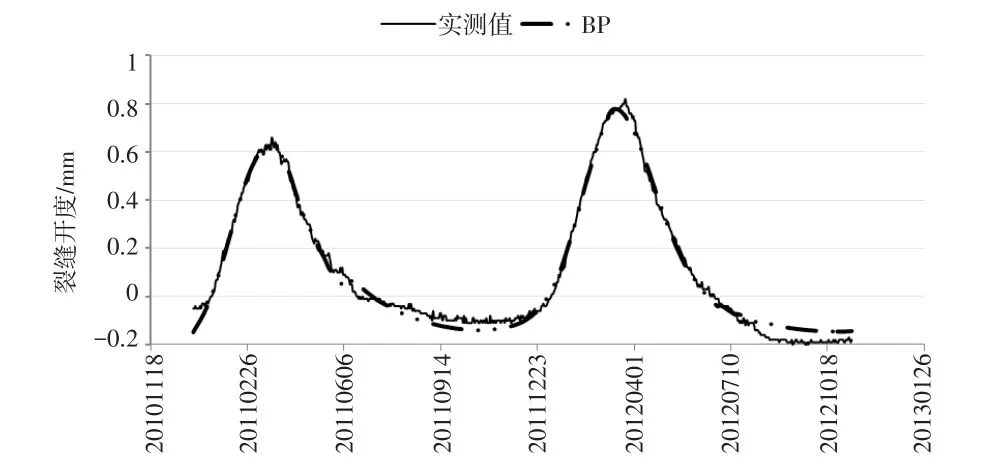
图1 BP神经网络训练结果对比Fig.1 Comparison between the BP neural network training re⁃sult and the measured data
(2)由于数据集中各个变量的差异较大,不属于同一个数量级,因此,必须对样本数据进行归一化处理。实际分析发现,隐含层神经元个数对ELM性能影响较大,ELM模型中神经元个数取70,训练和仿真效果最好。由图3分析得,ELM训练集拟合曲线基本与实测曲线重合,ELM模型拟合效果很好。
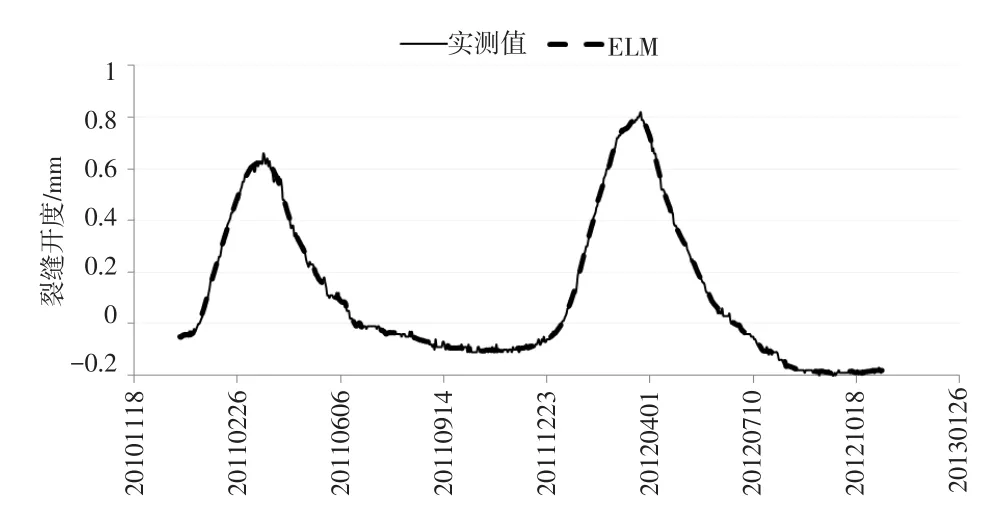
图2 ELM训练集结果对比Fig.2 Comparison between the ELM training result and the measured data
ELM模型在训练过程中只需设置隐含层神经元的个数,便可以获得唯一的最优解,与传统的BP模型相比,调节参数少、学习速度快、效率高。同BP神经网络一样,算法随机产生输入层与隐含层间的连接权值及隐含层的阈值,训练和仿真结果不稳定,需进行多次训练,取其最优结果。
(3)SVR模型进行数据训练时,先要对样本数据进行归一化处理。实际训练时,核函数对模型性能有较大影响,RBF核函数对应的模型泛化能力最好,与线性及Sigmoid核函数相比,尽管多项式核函数对应的模型训练性能较好,但其泛化能力较差。由图3知,SVR模型训练拟合效果非常好,精度很高。
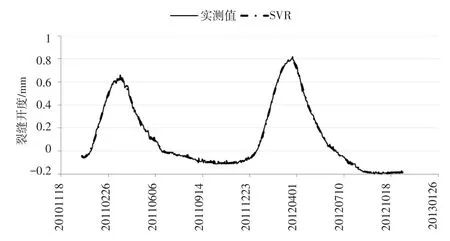
图3 SVR训练集结果对比Fig.3 Comparison between the SVR training result and the measured data
SVR的拓扑结构由支持向量决定,不像神经网络那样具有随机性,避免了传统神经网络需要反复试凑,确定网络结构的问题。
(4)BP、SVR、ELM模型的预测精度如表1所示:3种模型的决定系数R2都较高,均方误差MSE都比较小,符合要求;SVR模型的决定系数R2要略高于 BP神经网络和 ELM 模型(0.928>0.919>0.916)。在运行时间方面,ELM模型训练和仿真速度最快,只有0.161 s,大大快于BP和SVR。BP神经网络为8.618 s,而SVR模型实际上是个二次规划问题,训练实质是不断优化的过程,运行时间较长,为517.820 s。分析比较得,ELM学习速度性能最优,SVR预测精度最高,但由于其运行速度限制,目前适合于处理小规模问题。

表1 BP、SVR、ELM模型预测精度对比Table 1 Comparison of the prediction accuracies of BP,SVR and ELM model
(5)BP、SVR、ELM模型的预测结果对比如图4所示。比较曲线,BP神经网络预测曲线趋势与实测曲线“一致”,这是由于BP通过“记忆”训练样本的趋势来预测后面的趋势,能预测较长时间序列;SVR模型总体预测效果最优,与实测值曲线最“靠近”;ELM模型预测临近短时间内测值精度很高,但预测曲线的趋势渐渐偏离实测值,只适合预测短期序列。
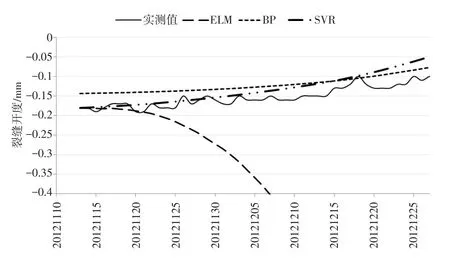
图4 BP、SVR、ELM预测结果对比Fig.4 Comparison of the prediction results of BP,SVR and ELM model
3 结语
由BP神经网络、ELM、SVR分别建立大坝裂缝开合度模型,通过对比分析得到以下结论:
(1)智能算法应用于大坝安全监控模型,结合计算机技术优点,精度较高,运算效率快,具有较好的发展前景。
(2)SVR模型拓扑结构稳定,预测精度较高;ELM模型调节参数少、学习速度快、泛化性能好,应用方便;BP神经网络能很好记忆数据的趋势,长期序列预测效果好。
(3)根据ELM模型预测短期序列较优的特点,可探索在线学习ELM方法,根据更新的实测数据及时动态进行预报;继续探索SVR求解大规模问题算法,提高其运行速度。
[1]梅一韬,何鹏.3种混凝土坝坝基扬压力监控模型的比较[J].河海大学学报(自然科学版),2010,38:361-364.
[2]顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.
[3]苏怀智.大坝安全监控感智融合理论和方法及应用研究[D].河海大学,2002.
[4]宋志宇.基于智能计算的大坝安全监测方法研究[D].大连理工大学,2007.
[5]吕蓓蓓,杨远斐.偏最小二乘法与神经网络耦合的大坝监测模型[J].人民黄河,2013(3):84-85,89.
[6]周洪波.基于人工神经网络的大坝变形监测正反分析研究[D].武汉大学,2004.
[7]张飞.基于粒子群的BP神经网络在大坝变形预测中的应用研究[D].辽宁工程技术大学,2011.
[8]张伟,吴丹,李小奇,胡晓雨.基于最小二乘支持向量机的大坝应力预测模型[J].水利与建筑工程学报,2011,9(1):26-29.
[9]谈小龙.基于边坡位移监测数据的进化支持向量机预测模型研究[J].岩土工程学报,2009(5):750-755.
[10]蒋国芸,郄志红,王东君,张俊杰.大坝安全监测的鲁棒最小二乘支持向量机模型[J].水利水电技术,2012(2):86-89.
[11]潘华贤,程国建,蔡磊.极限学习机与支持向量机在储层渗透率预测中的对比研究[J].计算机工程与科学,2010(2):131-134.
[12]胡义函.基于稳健估计的极限学习机方法研究[D].湖南大学,2012.
[13]史峰,王辉,胡斐,郁磊.Matlab智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.
[14]谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010.
[15]王薇.MATLAB从基础到精通[M].电子工业出版社,2012.
[16]ZHU Q Y,QIN A K,SUGANTHAN P N,et al.Evolutionary Extreme Learning Machine[J].Pattern Recongnition,2006,70:489-501.
[17]黄红女,周琼,华锡生.大坝安全监控理论与技术研究现状综述[J].大坝与安全,2005(2):54-57,71.
[18]吴中如.大坝的安全监控理论和试验技术[M].北京:中国水利水电出版社,2009.
