遗传扩展蚁群算法用于马斯京根模型参数估计

赵红杰，柏继云，马力

（1.东北农业大学理学院，哈尔滨 150030；2.东北农业大学工程学院，哈尔滨 150030）

遗传扩展蚁群算法用于马斯京根模型参数估计

赵红杰1，柏继云1，马力2

（1.东北农业大学理学院，哈尔滨 150030；2.东北农业大学工程学院，哈尔滨 150030）

文章针对扩展蚁群算法收敛速度慢，易陷入局部最优缺点，对扩展蚁群算法提出改进策略，引入遗传算法产生初始解，加入局部细搜策略。根据解的权重改进解存储器中每个解权值，增加解的方向性，快速获得最优解，通过多个典型函数寻优确定方法有效性。利用改进后算法解决洪水演算马斯京根模型参数估计问题，通过与现有马斯京根模型参数估计方法对比，验证算法具有更好优化性能，为精确估计马斯京根模型参数提供更有效方法。

遗传算法；扩展蚁群算法；连续空间优化；马斯京根模型；参数估计

Dorigo等首次提出用于求解连续空间优化问题的最新蚁群优化算法—扩展蚁群算法（Extended ant colony algorithm-ACOE）[1-2]，该算法通过引入解存储器作为信息素模型，将基本蚁群算法的离散概率选择方式连续化，将蚁群算法扩展到连续空间优化问题上。ACOE按照蚁群算法框架设计，简单易行。但ACOE仍然采用随机方式产生初始解，初始信息素匮乏，仅通过一次搜索中解存储器中解的目标函数值的大小构建信息素，解方向不够明确，易陷入局部最优。因此，本文针对ACOE算法的缺点进行三点改进，引入能产生丰富解的遗传算法[3]产生初始解，并加入局部细搜策略避免陷入局部最优，根据解的重要性改进解存储器中每个解权值，增加解方向性，快速获得最优解，将此改进算法称为改进遗传扩展蚁群算法（Genetic algorithmextended ant colony optimization，GAACOE）。

马斯京根模型是河道洪水预报的重要模型并广泛应用[4]。马斯京根模型参数估计是运用马斯京根模型进行预报的前提。传统确定模型参数方法主要有试错法[5]、图解法[6]、最小二乘法[7]等计算量大、计算过程繁琐、受经验制约等，结果精度不高。近年来，智能优化算法逐步应用到流域水文模型参数的率定优选上。常用的有遗传算法、粒子群算法等[8-11]，这些算法克服水文系统受天文、气象、气候、下垫面、人文活动等众多因素影响而表现出的高维、多峰值、非线性、不连续、非凸性和带噪声等复杂特征，对流域水文模型参数进行全局优选，寻找最优解。本文采用改进的遗传扩展蚁群算法优化参数，并与这些智能算法对比，验证其优越性和实用性。

1 遗传扩展蚁群算法

1.1 扩展蚁群算法简介

ACOE算法主要包括初始化解存储器、通过高斯核概率密度函数构造可行解及信息素更新3个步骤[1-2]。

1.1.1 解存储器初始化

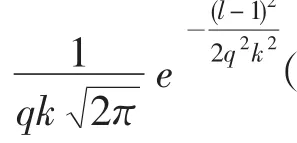
表1 ACOE的解存储器结构Table 1 Archive of solutions kept by ACOE

1.1.2 对高斯核概率密度函数采样构建可行解

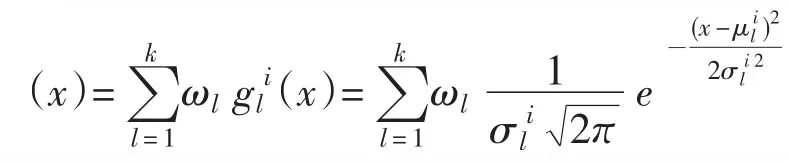
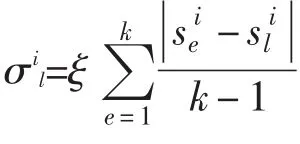
1.1.3 信息素更新

将上面m只蚂蚁采样得到的m个解向量与原解存储器T中的解一起组成一个临时解向量，并将这个临时解向量按目标函数排序，取前K个解向量加入解存储器T里，以保持其长度K不变。确保只有最优解能够存储在解存储器中，使解存储器里的解能更好地引导搜索。

1.2 改进遗传扩展蚁群算法

1.2.1 利用遗传算法产生初始解

遗传算法[3]是以达尔文的生物进化论和孟德尔的遗传变异理论为基础构建的一种概率搜索算法，将问题的可行解编码为一个二进制串，称之为染色体。遗传算法首先生成多个初始染色体种群，并基于种群反复迭代执行选择、交叉、变异的遗传操作获得问题的最优解[12]。遗传操作可以使问题很快收敛到问题的较优解，但遗传算法缺少反馈操作，很难获得全局最优解。因此本文利用遗传算法产生ACOE算法的初始解信息，利用遗传算法快速的全局搜索特性，获得ACOE算法的初始解存储器。

设置遗传算法迭代次数为t（tb＜t＜tc），其中tb为最小遗传迭代次数，tc为最大遗传迭代次数。计算每次迭代时的进化率R=-fi（s）--fi+1（s），如果连续3代进化率R均满足0＜R＜Rmin，则终止遗传算法，进入蚁群算法。其中-fi（s）为遗传算法第i次迭代后得到的适应度函数平均值，Rmin为给定的最小阈值。

1.2.2 在ACOE算法中增加局部细搜索

ACOE算法的另一个缺点是算法容易陷入局部最优，为避免算法陷入局部最优，同时也为增加搜索精度，本节引入变尺度局部细搜索策略，在迭代的每一步对ACOE算法迭代最优解进行局部细搜。

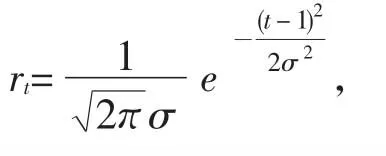
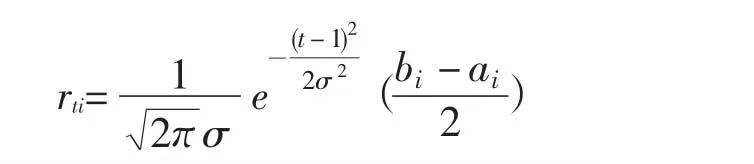
式中，t为迭代次数，aj≤Xj≤bj，j=1，2，…，n是优化问题解空间，很显然，rti会随着迭代次数的增加而单调递减，因而称为变尺度搜索，然后，在搜索区域内利用均匀分布随机产生一定数量的解，对刚产生的自变量，进行函数值比较，若找到优于全局的最优蚂蚁，则设为全局最优蚂蚁。

1.2.3 解存储器的构建和更新

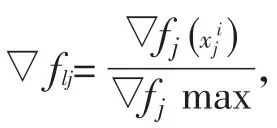
1.3 遗传扩展蚁群算法（GAACOE）流程

Step1：GA初始化：选取种群规模M，概率Pc和Pm，最大迭代次数、最小迭代次数、最小进化率R，以随机分布产生M个初始种群。

Step2：对个体进行适应度评价，适应度函数取为目标函数值；

Step3：进行遗传操作产生新的群体；

Step4：返回Step2，对新群体解码进行适应度评价；

Step5：由最小最大迭代次数或最小进化率决定算法终止时刻，若满足条件，转Step6，否则转Step3；

Step6：将遗传算法获得的最优解作为ACOE解存储器的初始解：在遗传算法最后一代选择适应函数最高的K/2个个体组成一个矩阵S1，同时以均匀分布随机产生K/2个个体组成矩阵S2，与S1合成一个维数为K×N的新矩阵S，N为决策变量的维数；

Step7以矩阵为解存储器的初始解，利用扩展蚁群算法ACOE求解，在每一次迭代后，利用式（4）求半径执行局部细搜策略，运行ACOE算法G代。

2 仿真分析

本文应用改进扩展蚁群算法（GAACOE）和扩展蚁群算法（ACOE）以及标准遗传算法（SGA），选用典型函数进行仿真实验，所有仿真均在奔腾4 CPU和MATALAB 7.0环境下运行。为了便于比较，本文仍然选择文献[1]实例。

2.1 参数选择

对照文献[1]，ACOE算法初始参数选择：蚂蚁数目m=70，解存储器容量K=45，参数ξ=1，q= 0.001。SGA参数：种群规模为M=50，轮盘赌选择，单点交叉，单点变异，交叉概率pc=0.90和变异概率pm=0.10-[1:1:M]·（0.01）/M。GAACOE参数选择：遗传部分参数取种群规模为M=35，交叉概率pc=0.90和变异概率Pm=0.10-[1:1:M]*（0.01）/M，最大迭代次数200、最小迭代次数100、最小进化率R=10；ACOE算法部分蚂蚁数目m=70，解存储器容量K=45，参数ξ=1，q=0.0001。限定步数均为max= 400。

2.2 Rosenbrock（R5）函数

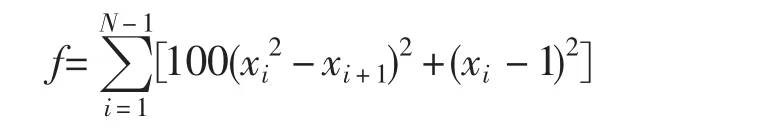
N=5，-10≤xi≤10，该函数形势复杂，决策变量较多，搜索空间较大，当xi=1时取得全局最小值0，当函数值为0.0001时取得成功。

分别用GAACOE、ACOE、SGA对该函数求全局最小值进行10次仿真，仿真结果对比见表2。

图1是利用GAACOE算法对Rosenbrock（R5）函数做400次寻优，从图中可以看出，GA和改进ACOE算法在110代进行了交接，算法利用GA产生的最优种群和一部分随机产生的种群，构成ACOE算法的初始解存储器，利用加入局部细搜策略的ACOE算法进行余下迭代。ACOE算法利用GA提供的丰富初始种群信息，迅速获得Rosenbrock（R5）的最优解，加入的局部细搜策略使迭代速度更快。

为比较算法优劣，利用GAACOE、ACOE、SGA方法分别对Rosenbrock（R5）函数做10次试验，每次仍然迭代400次，图2是利用3种方法获得的平均性能曲线。由图2可知，遗传算法产生的初始解非常丰富，平均值并不低，但是当采用扩展蚁群算法进行迭代后，丰富的初始解产生作用，ACOE很快收敛到最优解，说明初始信息素积累的重要性。表明，经过遗传算法确定初始种群后的改进扩展蚁群算法方向明确，收敛速度快，而且搜索全局最优解的能力很强。

表2 函数极值问题优化结果(10次试验)Table 2 Optimization results of function extremum(10 experiments)

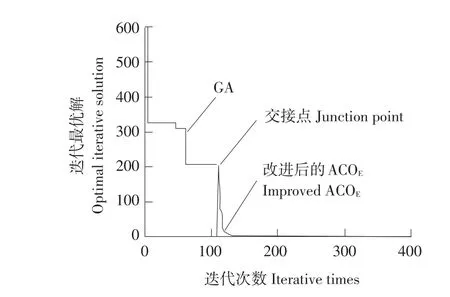
图1 最优解曲线Fig.1 Optimal solution curve

当决策变量数量更多时，取N=10，即Rosenbrock（R10）函数，运行ACOE算法10次，每次迭代1 000次，最优解│f1（x）│≤0.02的次数为0次，迭代2 000次，获得最优解的次数是3次；运行GAACOE算法迭代1 000次，运行算法10次，获得最优解的次数是8次，说明GAACOE算法对于求解维数较多的连续函数具有较强的寻优能力。

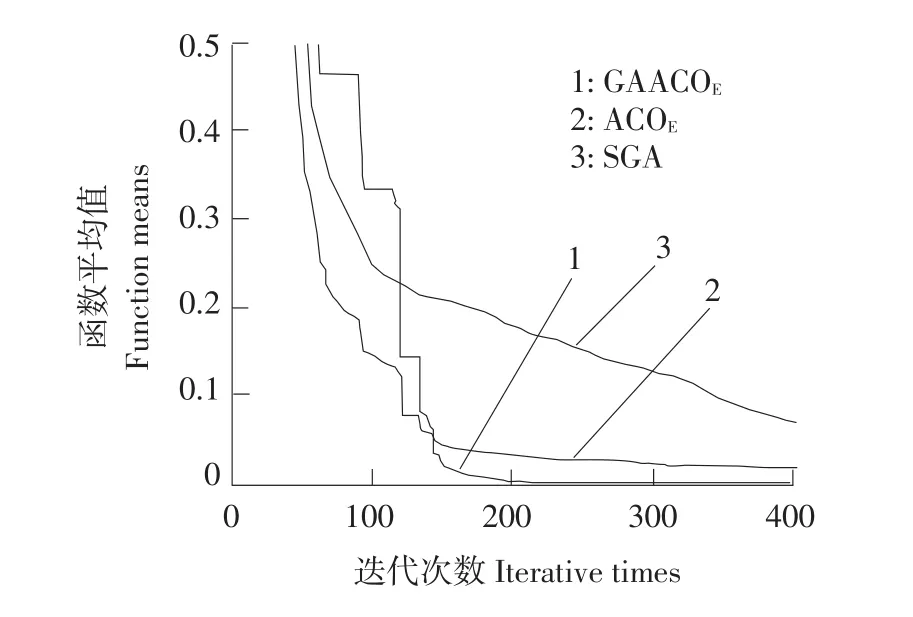
图2 平均适应度曲线Fig.2 Average fitness curve

3 马斯京根模型参数优化

3.1 马斯京根模型介绍

河道洪水演算包括水力学和水文学两类方法。水力学方法以圣维南方程组的求解为基础，适用于有准确河道地形和河床观测数据的河段，当这些资料条件缺乏时，水文学方法就成为洪水演算的另一种重要方法。在水文学中，马斯京根（Muskingum）法是河道洪水演算的一种重要方法。马斯京根法由Mc.Carthy提出，并在美国马斯京根河上首先应用，马斯京根法依据的基本原理为水量平衡方程和槽蓄方程[8-11]，基本方程为：

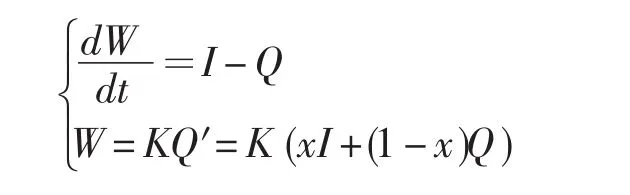
式中，W为河段的槽蓄量，t为时间，I和Q分别为河段的入流量、出流量，Q为储流量，x和K分别为流量比重因子和槽蓄系数。将上式的微分方程离散化后得到离散的差分形式为：

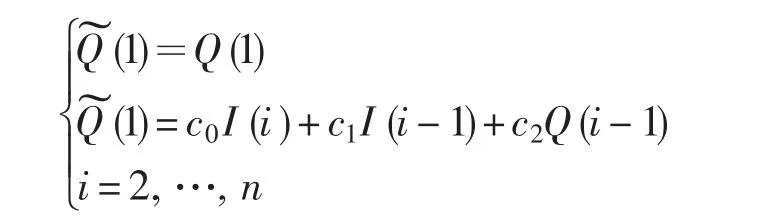
式中，Q（i）和Q（i）分别为第i个演算时段的演算出流量和实测出流量，I（i）为第i个演算时段的入流量，n为演算时段个数，c0，c1和c2为流量演算系数，且满足c0+c1+c2=1。显然，使用马斯京根模型的一个重要问题是模型参数c0，c1和c2的估计，并且该最优估计问题是一个非线性的参数优化问题。

3.2 马斯京根模型参数优化对比

本文选用与文献[8-11]相同的适应度函数，并采用相同的实例，进行比较。

3.2.1 优化的适应度函数

优化模型：

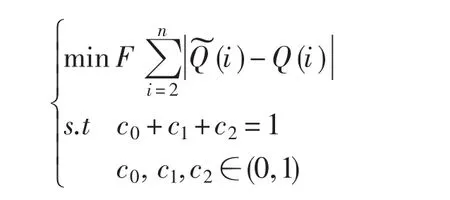
优化的适应度函数：

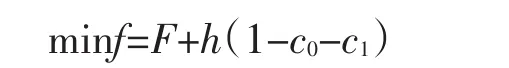
上式中，h（1-c0-c1）为惩罚项，当约束条件1-c0-c1∈（0，1）满足时其取值为0，否则取值为106。

3.2.2 应用实例

以文献[13]中的例2南运河称钩湾至临清段河段1960年8月的一次洪水过程资料为例，该河段长83.8 km，中间无支流汇入，两岸有大堤控制，在输水时沿岸有堤水灌溉，较大降雨时有涝水排入，但对洪水的影响很小，演算时段取12 h。

GAACOE初始参数选择：蚂蚁数目m=70，解存储器容量K=45，参数ξ=1，q=0.0001，转角步长初值θ0=0.05π，变异概率pm=0.05。限定步数仍为Max=500。重复运行10次。

将优化结果与文献[8-11]中的改进粒子群算法（APSO）、免疫粒子群算法（IPSO）、蚁群算法（ACO）进行对比，结果见表3。

从表3中所列的各项指标看，遗传扩展蚁群算法（GAACOE）演算流量的平均绝对误差和平均相对误差都较其他算法有大幅度减少。由此可见，使用遗传扩展蚁群算法对马斯京根模型参数进行优化的精度很高。

表3 马斯京根模型各参数估计方法的结果比较（1960年）Table 3 Parameters of Muskingum model by using different methods(1960 year)

根据1960年的洪水分析得到三组流量演算系数对1961年称钩湾的入流过程进行演算，将文献[8-11]的方法改进粒子群算法（APSO）、蚁群算法（ACO）、多智能体遗传算法（MAGA）和本文方法的计算结果列于表4。从表4中所列的各项评价指标来看，本文方法比其他算法具有更好的优化性能，求得的适应度函数值、平均绝对误差和平均相对误差等评价指标均小于其他算法。

由表3、4可见，改进遗传扩展蚁群算法就演算出流量过程与实测出流量过程的拟合综合效果而言，本文算法的求解结果明显优于改进粒子群算法（APSO）、免疫粒子群算法（IPSO）、蚁群算法（ACO）、多智能体遗传算法（MAGA）等优化方法，可应用于各种自然灾害模型的优化问题。

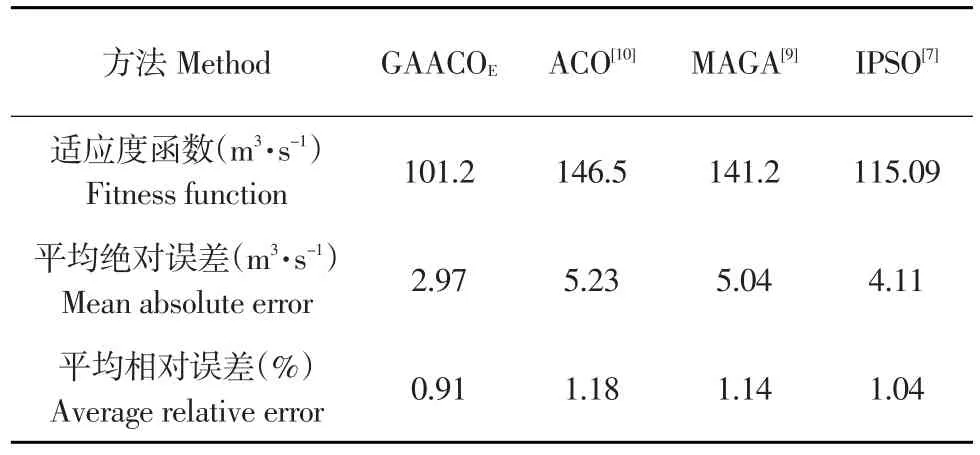
表4 南运河称钩湾至临清段河段各参数估计方法的流量演算结果比较（1961年）Table 4 Flow routing results of the Nanyunhe River by using different methods(1961 year)

4 讨论与结论

本文结合遗传算法和扩展蚁群算法优点，提出新的改进遗传扩展蚁群算法（GAACOE）。遗传扩展蚁群算法使用遗传算法产生初始解，避免解单一性。本文针对扩展蚁群算法仅通过解存储器中解的目标函数值大小构建信息素的不足，根据解重要性给出解存储器中每个解权值以增加解方向性，使算法能快速获得最优解，并在每次迭代中加入变尺度局部细搜策略，能够快速有效地跳出局部最优解。

本研究结果表明，GAACOE算法在收敛速度和收敛精度上均优于ACOE、SGA算法。本文将这种算法应用于洪水演算马斯京根参数估计最优化问题。设计非参数优化估计模型，利用扩展蚁群优化寻优，演算出流量过程与实测出流量过程的拟合程度为优化准则，使演算流量接近实际。

[1]Socha K,Dorigo M.Ant colony optimization for continuous domains[J].European Journal of Operational Research,2008,185 (3):1155-1173.

[2]李士勇,柏继云.连续函数寻优的改进量子扩展蚁群算法[J].哈尔滨工程大学学报,2012,33(1):80-84.

[3]Holland J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan Press,1992.

[4]芮孝芳.Muskingum法及其分段连续演算的若干理论探讨[J].水科学进展,2002,13(6):682-688.

[5]王光生,宁方贵,肖飞.实用水文预报方法[M].北京:中国水利水电出版社,2008.

[6]长江水利委员会主编.水文预报方法[M].北京:水利电力出版社, 1993.

[7]翟国静.马斯京根模型参数估计方法探讨[J].水文,1997(3):40-43.

[8]李明明,李承军,张铭.改进PSO法在马斯京根模型参数估计中的应用[J].人民长江,2008,39(3):60-62.

[9]甘丽云,付强,孙颖娜,等.基于免疫粒子群算法的马斯京根模型参数识别[J].水文,2010,30(3):43-46.

[10]鲁帆,蒋云钟,王浩,等.多智能体遗传算法用于马斯京根模型参数估计[J].水利学报,2007,38(3):289-294.

[11]詹士昌,徐婕.蚁群算法在马斯京根模型参数估计中的应用[J].自然灾害学报,2005,14(5):20-24.

[12]王晓红.蚁群算法与遗传算法结合使用方法论[J].中国水运, 2008,8(8):131-132.

[13]翟国静.马斯京根流量演进系数的直接优选法[J].河北工程技术高等专科学校学报,1996(2):6-11.仪器仪表学报,2005:1135-1139.

Genetic extended ant colony algorithm for parameter estimation of Muskingum routing model

ZHAO Hongjie1,BAI Jiyun1,MA Li2(1.School of Science, Northeast Agricultural University,Harbin 150030,China;2.School of Engineering,Northeast Agricultural University,Harbin 150030,China)

According to extended ant colony algorithm converging slowly and easily falling into local optimum,it presented some improved strategies:introduced genetic algorithm to produce the initial solution and join the local fine search strategy to avoid ants in local optimum and the weight of each solution improved by its'importance of the memory to get the optimal solution quickly and increase the direction.This paper used the improved algorithm to solve flood routing problem by parameter estimation of Muskingum routing model，by comparison with the existing parameter estimation of Muskingum routing method,validated algorithm has better optimize performance,and provide a more effective way to accurately estimating the parameters of Muskingum routing model.

genetic algorithm;extended ant colony algorithm;optimization of continuous space; Muskingum routing model;parameter estimation

TP18

A

1005-9369（2014）08-0118-06

2013-04-24

黑龙江省青年科学基金（QC2011C045）

赵红杰（1977-），女，讲师，硕士，研究方向为应用数学。E-mail:zhaohongjie77@163.com

时间2014-7-18 15:02:04[URL]http://www.cnki.net/kcms/detail/23.1391.S.20140718.1502.009.html

赵红杰,柏继云,马力.遗传扩展蚁群算法用于马斯京根模型参数估计[J].东北农业大学学报,2014,45(8):118-123.

Zhao Hongjie,Bai Jiyun,Ma Li.Genetic extended ant colony algorithm for parameter estimation of Muskingum routing model[J].Journal of Northeast Agricultural University,2014,45(8):118-123.(in Chinese with English abstract)