基于MapGIS的含量-面积法确定地球化学异常下限

陈杜军，张 恒，张玉宝

(内蒙古地质矿产勘查院，内蒙古呼和浩特 010011)

0 引言

地球化学异常下限的确定是勘查地球化学矿产勘查和资源预测的一项基本内容，也是环境地球化学异常辨析与环境评价的重要依据。传统的均值标准差法要求数据符合正态分布或对数正态分布，并人为剔除离群点，一般采用平均值与n倍标准差之和作为异常下限，即T=X+nSd(n=1－3)。新的研究表明元素的地球化学分布并不局限于正态分布或对数正态分布［1］，李长江等(1995)揭示地球化学景观是具有低维吸引子(D=2.9)的混沌系统，具有典型的分形特征，可以进行分形处理［2］。

1 分形模型原理及含量-面积法

设分形模型:

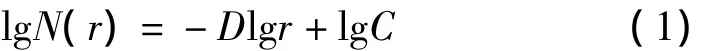
式中:r为特征尺度;N(r)为尺度大于等于r的和数;C＞0，为比例常数;D ＞0，为分维数。

将观测数据N(ri)和ri两组数据代入，散点大致分布在两段直线上，用最小二乘法分段拟合的方法，找出合适的分界点r0，使各区间拟合的直线与原始数据之间的剩余平方和Ei(i=1，2)在两个区间的总和为最小，即:

式中:ri0为分界点;D1和D2分别为相应区间的斜率，即分维数。通常，应对每个回归方程进行相关系数及方差分析检验，以此检验回归方程的显著性［3］。

成秋明等(1994)基于分形的观点提出了确定地球化学异常的含量-面积法［4］，其模型为:

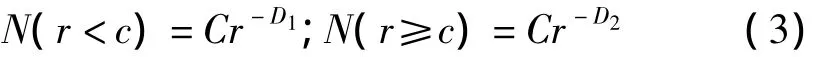
式中:c为元素含量值;r为分界点，其地球化学意义在于元素含量在空间上至少存在两个层次的分布，即存在背景分形分布和异常分形分布［5－6］，分界点 r对应的元素含量值即为异常下限值。

2 含量-面积法应用实例

2.1 均值标准差法计算异常下限

内蒙古阿拉善某测区共取得土壤化探样品2 525件，以Ag元素数据为例，采用Q-Q图进行正态分布检验(图1)，原始数据及其自然对数值均偏离正态分布。

对原始数据进行离群数据(最高值、最低值)的迭代处理后用异常下限公式T=X+nSd(n=2)计算Ag元素异常下限为0.25 ng/g。

2.2 含量-面积法计算异常下限

通过MapGIS的DTM分析模块，绘制元素含量的平面等值线图，生成一个包含起始值、终止值和面积属性的区文件。通过MapGIS的空间分析模块的检索和属性统计功能，选取不同的起始值r，统计各r值所围成的平面面积N(r)。空间分析系统求出的Ag元素数据(n=2 525)的N(r)见表1。

对表1中不同r值及其对应取的面积数据N(r)取对数，用相关软件(如Excel、Grapher等)对数据进行处理。用最小二乘法拟合成两段直线，所得的直线方程分别为:

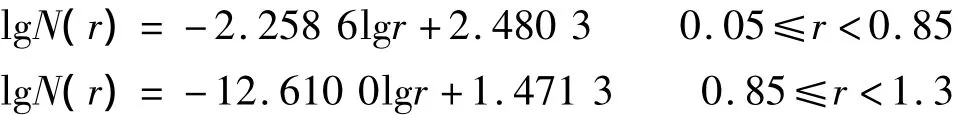
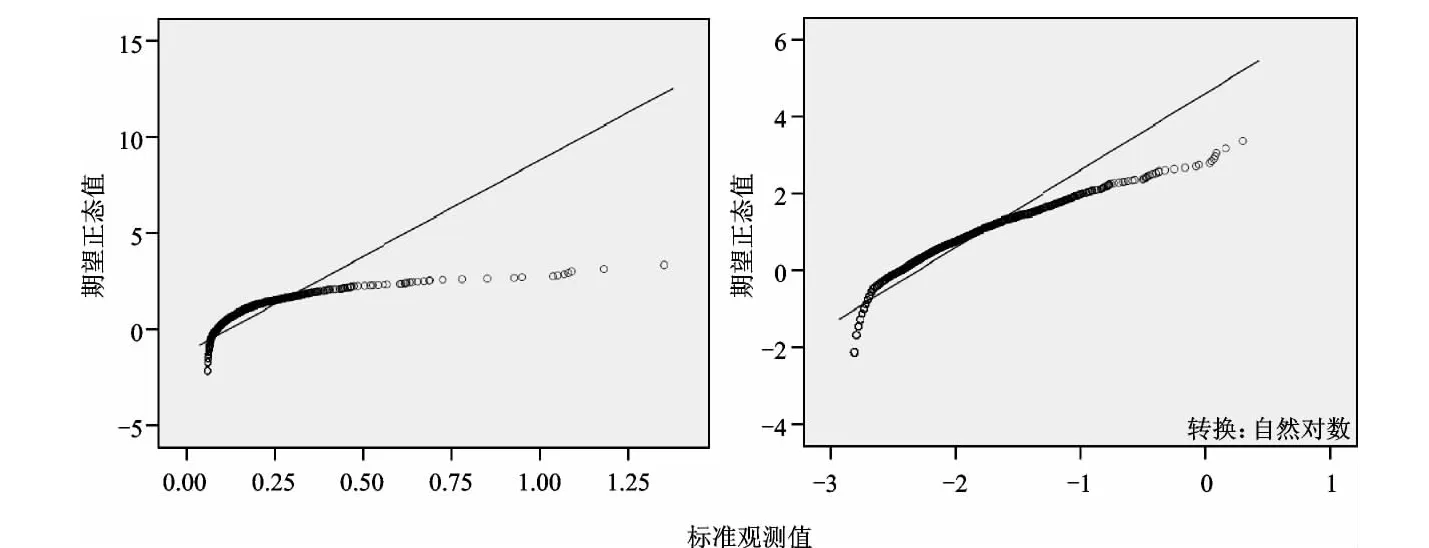
图1 Ag元素数据Q-Q图Fig.1 Q-Q diagram of Ag data

表1 空间分析系统求出的Ag元素数据的N(r)Table 1 The N(r)of Ag data calculated by spatial analysis

两个区间的剩余平方和(E=E1+E2)为0.461，其中分界点为 r16，分维数 D1=2.258 6，D2=12.610 0。lg r－lg N(r)分布直线拟合见图2。

图2 Ag元素lg r－lg N(r)分布直线拟合图Fig.2 The lg r－lg N(r)distribution fitting plot of Ag data

对以上两个方程进行显著性检验，拟合直线的相关性判定系数R2分别为0.984 0和0.954 1，表明所拟合的直线能够很好地反映元素的分形分布趋势。在含量-面积分布曲线上，两段拟合直线的过渡阶段有明显突变，表明该区土壤Ag含量数据具有背景分形分布和异常分形分布的临界点。两段直线交点所对应的Ag含量为0.68 ng/g，即为该区土壤Ag的异常下限值。

为得到更加精确的计算结果，适当加密拐点两侧分类的面积数，将r值步长由0.05加密至0.01(r=0.80～0.90)。加密区间 lg r－lg N(r)分布直线拟合见图3。经校正，计算该区土壤Ag异常下限为0.6 ng/g。

2.3 应用效果对比

以测区Ag、Cu两种元素为例，对比均值标准差法与含量-面积法确定的异常下限及圈定的异常区域，效果见图4。

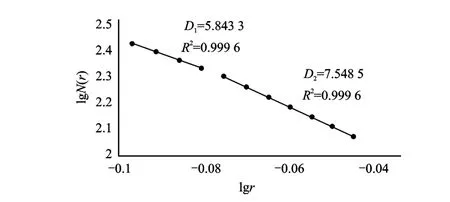
图3 加密区间Ag元素的lg r－lg N(r)分布直线拟合图Fig.3 The lg r－lg N(r)distribution fitting plot of Ag data in concentrated area

由图4可知，均值标准差法所确定的异常下限值低于含量-面积法所确定的异常下限，表明前者本身有缺陷，离群点的剔除减小了异常下限的值。此外，测区南部大面积的第四系覆盖降低了元素平均值，含量-面积法仅将低值数据形成的面积限定在小范围内，可以避免同一测区中不同地球化学景观对元素空间分布造成的影响差异。

在化探异常显著的情况下，含量-面积法可以提高对区域异常的分辨力，减少异常查证的面积进而迅速定位靶区，但有可能在化探异常不显著的情况下漏掉有用的弱异常信息。结合区域地质背景和成矿条件，本区化探异常主要受下元古界二道凹群、二叠系下统大红山组、三叠纪花岗(斑)岩体和北东及北北东向断裂构造控制，下元古界二道凹群地层作为各元素富集的矿源层，二叠系下统大红山组是Ag、Cu、Zn等元素成矿的有利赋存层位，三叠纪花岗(斑)岩中主成矿元素丰度高、分异性强，易富集成矿。紧邻本测区的下元古界二道凹群和二叠系下统大红山组火山岩地层中已发现Ag、Cu、Mo等多金属矿点、矿化点多处，图4中测区北部Cu元素弱异常不应被忽略。

3 讨论

(1)传统的均值标准差法要求地球化学数据呈正态分布或对数正态分布;含量-面积法基于数据服从分形分布，更能体现地球化学数据的原始特征。

图4 均值标准差法与含量-面积法效果对比Fig.4 Comparison of effects of mean-standard deviation method and content-area method

(2)均值标准差法与含量-面积法所确定的异常下限有一定的偏差，均值标准差法在数据处理时人为剔除离群点减小了异常下限的值;而含量-面积法将离群数值所形成的面积限定在小范围内，仅影响周围，不对数据整体产生重大影响。

(3)为得到更加精确的计算结果，可适当加密拐点两侧分类的面积数。

(4)含量-面积法可以减少异常查证的面积进而迅速定位靶区，但也可能漏掉有用的弱异常信息。在实际工作中，应结合区域地理地质背景，使用多种方法共同确定异常下限。

［1］ 韩东昱，龚庆杰，向运川.区域化探数据处理的几种分形方法［J］.地质通报，2004(4):714－719.

［2］ 李长江，麻土华，朱兴盛，等.矿产勘查中的分形、混沌与 ANN［M］.北京:地质出版社，1999:1－140.

［3］ 李随民，姚书振.基于MAPGIS的分形方法确定化探异常［J］.地球学报，2005，26(2):187 －190.

［4］ 成秋明.多维分形理论和地球化学元素分布规律［J］.地球科学，2000，25(3):311 －318.

［5］ 孙忠军.矿产勘查中化探异常下限的多重分形计算方法［J］.物探化探计算技术，2007，29(1):54 －57.

［6］ 戴慧敏，宫传东，鲍庆中，等.区域化探数据处理中几种异常下限确定方法的对比——以内蒙古查巴奇地区水系沉积物为例［J］.物探与化探，2010，34(6):782 －786.