边界元法计算复合材料的双向拉伸强度①

蔡登安，周光明，曹 然，黄 翔

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

0 引言

纤维增强复合材料以其轻质、高强、抗疲劳、减振、耐高温及可设计等一系列优点，在航空航天、能源、交通、机械和建筑等部门日益获得了广泛应用。一般而言，构件中复合材料多受双向或多向应力状态［1］。复合材料的测试技术已能准确表征纤维增强复合材料的单向力学行为。然而，同样的试验方法并不能完全适用于复合材料多向甚至只是双向响应问题［2］。对于受复杂应力状态的复合材料，仅仅研究其单向载荷下的强度是远远不够的。因此，不管是对强度准则进行试验验证，还是从损伤角度探讨复合材料在复杂应力状态下的破坏，都需要对复合材料试样进行双向加载研究。获得双向应力状态的传统方式是采用圆管形试件，目前更多的研究者把焦点放到了十字型试样上［3－4］，其优点在于十字型试样双向拉伸试验能直观地反映板壳复合材料的双向受力状态，因而成为当下最受重视的一种双向拉伸试验方法。

边界元法(BEM)是一种将研究的连续体区域的边界划分成有限个单元的数值方法，在某些领域已经成为工程设计的重要工具［5－6］。相比有限元法(FEM)，边界元法针对一些问题的分析有着独特的优点。Lachat和Watson［7］为边界元法作为一种有效数值方法的研究作出了贡献:他们提出了一种类似于有限元法的等参方法，并证明边界元法可作为解决具有复杂构型问题的一种有效工具。借助边界元方法，Pineda León等［8］研究了在不同温度和应力状态下材料的蠕变分析模型;刘云忠等［9－10］提出了正交各向异性复合材料裂纹问题的边界元分析方法;商欣萍等［11］用边界元法从理论上分析非织造土工织物的拉伸性能，与实验结果有较好的一致性;Araújo等［12］针对碳纳米管增强复合材料的微观结构分析，编写了边界元并行计算程序，并据此提出了一种可扩展的复合材料边界元并行计算代码;基于线性夹杂模型，Wang等［13］将边界元方法应用于纤维增强复合材料的3D大尺度热分析问题的研究中。

针对十字型试样双向拉伸实验研究，本文采用边界元法，从理论上研究了交织玻璃纤维增强复合材料的双向拉伸强度。建立复合材料双向拉伸边界元分析模型，并与有限元结果及试验结果进行比较，以期为复合材料双向拉伸强度研究提供一些理论依据。

1 边界元模型

1．1 基本方程

与长、宽尺寸相比，交织玻璃纤维增强复合材料十字型试样的厚度很小，故可将其看作是平面正交各向异性材料。平面正交各向异性问题的基本方程可描述如下:

平衡方程:

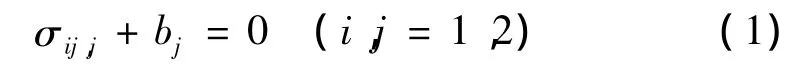
几何方程:

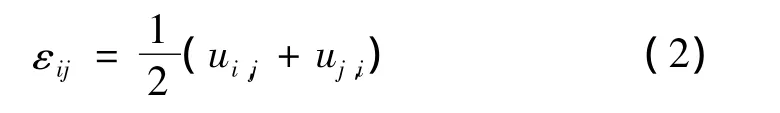
物理方程:

或

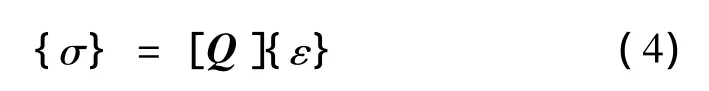
式中 ［S］和［Q］分别表示柔度矩阵和刚度矩阵，且［Q］=［S］－1。

平面正交各向异性材料有4个独立的弹性常数，即 E1、E2、ν12和 G12，分别表示交织玻璃纤维增强复合材料2个方向拉伸时的弹性模量、泊松比和剪切模量。交织玻璃纤维增强复合材料的柔度矩阵［S］可表示为

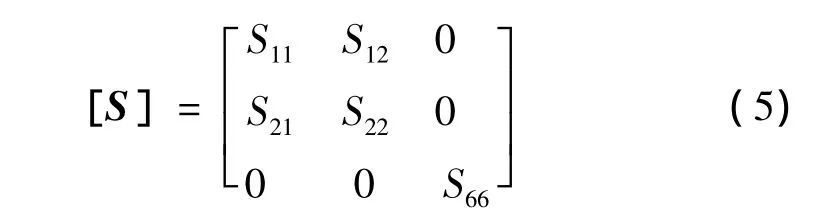
边界条件:

应力边界条件

位移边界条件

1．2 边界积分方程与基本解

边界元法的基础是用Fredholm［14］积分方程的位势积分来表示问题的解，它是将支配物理现象的微分方程转化成边界上的积分方程，然后再进行离散求解的数值计算方法。

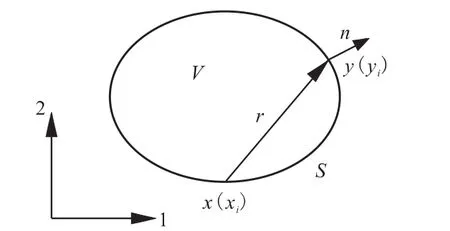
图1 平面区域V和边界SFig．1 Planar region V and boundary S

对于平面正交各向异性材料，如图1所示，由边界S所包围的平面区域上的任意点x的位移分量ui(x)，在不考虑体积力时，可由边界上各点y的位移分量和面力分量通过以下边界积分方程求得［5，11］:

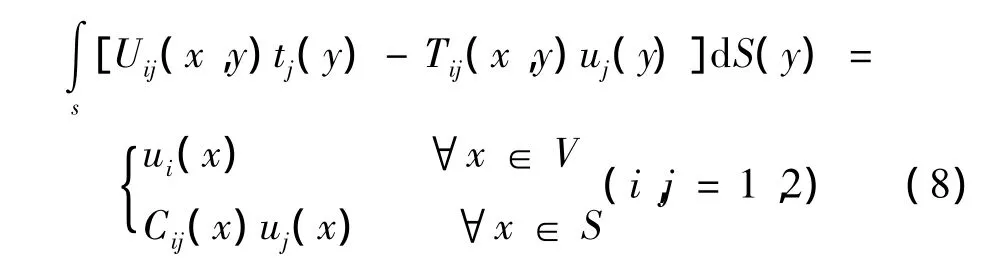
式中 ui和ti分别为位移和面力;Uij(x，y)和Tij(x，y)分别为平面正交各向异性材料的位移基本解分量和面力基本解分量。

系数Cij(x)的值与x点处边界形状有关，边界S光滑时，有

对于平面正交各向异性材料，位移和面力基本解可表示为［15］

其中，Kα、Ai、αi、Mi(i=1，2)为与弹性常数有关的参数;ri和θi分别为复平面中的矢径和幅角，且有

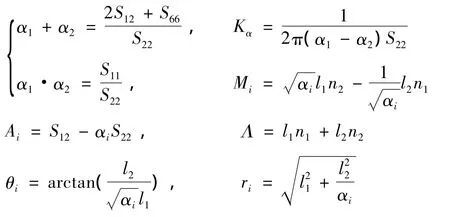
式中 l1、l2分别为y点与x点横、纵坐标之差;n1、n2分别为边界外法线的方向余弦。

1．3 积分方程离散化

通过边界积分方程，可求出边界上所有未知的位移和表面力分量。然而，通常情况下很难用解析方法求解积分方程，只能采用数值解法。将区域的边界划分成N(N=N1+N2)个简单单元。其中，N1个边界单元属于表面力已知，N2个边界单元属于位移已知，以N个边界单元上的积分之和表示整个边界上的积分。各边界单元上的位移和表面力，可通过插值函数与边界单元上有限个节点的位移和表面力以多项式近似。本文采用常单元将边界积分方程离散，单元节点取为边界单元中点，边界单元的位移和表面力等于单元节点的位移和表面力。

设 yi(i=1，2，…，N)为边界 Sj上的任意一点，对任意节点xi，边界积分方程可离散为

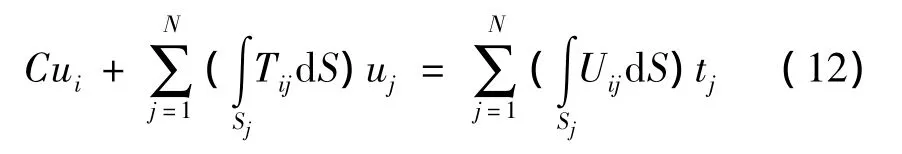
式中 下标i，j分别为第i、第j个单元。

设:

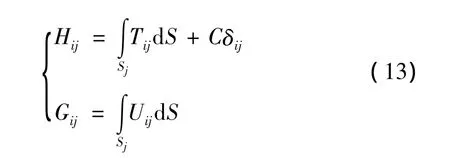
则对任意节点，边界积分方程可离散为

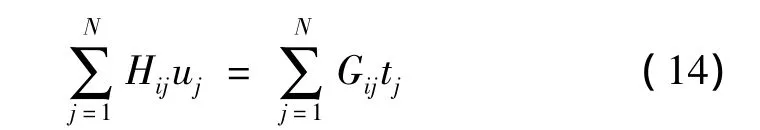
对于N个节点，根据各节点的离散化方程，可得到包含2N个方程的一次方程组，用矩阵形式可表示为

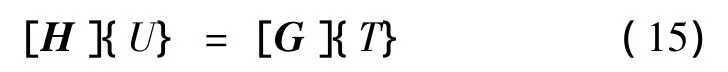
式中 ［H］、［G］均为2N×2N阶的位移和面力系数矩阵;{U}、{T}分别为边界单元节点的位移分量和表面力分量。

2 计算方法

根据以上理论分析，利用FORTRAN语言编写计算程序，来分析交织玻璃纤维增强复合材料双向拉伸强度，程序的计算流程见图2。计算前，要输入试样4个独立的弹性常数(纵向和横向的弹性模量、泊松比及剪切模量);同时，要输入试样的强度参数、几何尺寸、各单元的坐标以及边界条件。

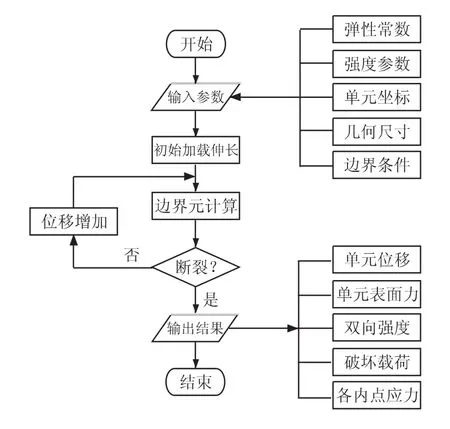
图2 程序计算流程图Fig．2 Flow-process diagram of program

交织玻璃纤维增强复合材料十字型试样的几何尺寸(单位:mm)，如图3所示。十字型试样中心36 mm×36 mm的正方形区域为中心试验区，该区域满足应力分布均匀，且应力水平较高，以保证初始破坏发生在中心试验区;同时，试验区剪应力远小于正应力，以至可忽略不计。受双向拉伸时，十字型试样在实际拉伸试验过程中，试样的AB端和CD端由夹头夹持在拉力作用下移动，EF端和GH端由夹头固定。与试验不同的是边界元理论计算时，为避免附加弯矩的影响，需释放EF端在1方向的位移约束和GH端在2方向的位移约束，如图4所示。若分别给AB端和CD端一个2方向和1方向上的伸长量，通过边界元法计算程序，便可得出十字型试样各自由边上边界单元的位移、各内点的位移和应力，以及达到该伸长量所施加的双向拉伸载荷。

对十字型试样进行单元划分，由于试件完全对称，为减少计算量，只需对1/4试样划分单元，如图5所示。

图3 十字型试样几何形状及尺寸Fig．3 Geometry and dimensions of cruciform specimen

图4 十字型试样的载荷与约束Fig．4 Loads and constraints of cruciform specimen

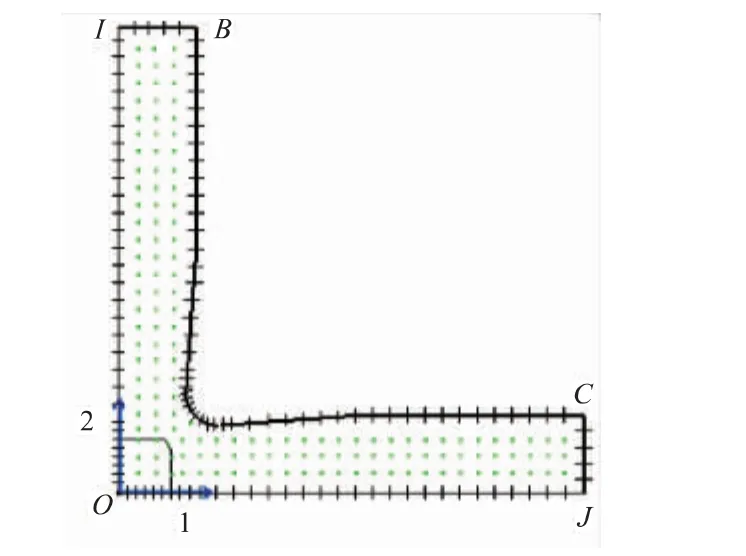
图5 十字型试样边界单元划分Fig．5 Boundary element of cruciform specimen

试样的OI边单元约束1方向的位移，OJ边单元约束2方向的位移;于IB与JC端作用原十字型试样拉伸载荷的一半。图中标记的各点为指定的内点。通过计算各指定内点的应力，可了解十字型试样在双向拉伸过程中的内力分布情况。

要计算交织玻璃纤维增强复合材料双向拉伸强度，需确定十字型试样断裂的条件，即试件在双向载荷下，拉伸到何种程度达到断裂。本文采用的强度准则为Tsai-Wu张量准则。平面应力状态下，Tsai-Wu张量准则可表述为

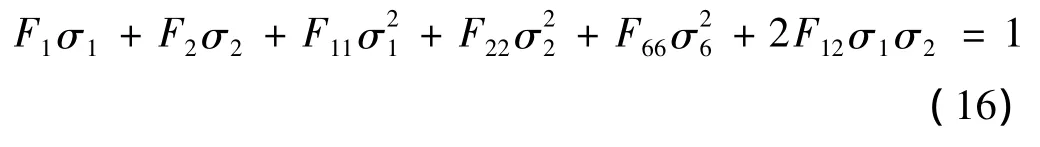
十字型试样中心试验区的剪应力较小，忽略不计，因而准则方程可简化为

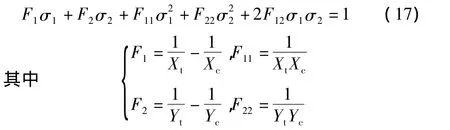
式中 Xt、Xc、Yt、Yc分别为材料纵向的拉压强度和横向的拉压强度，可由单向拉伸(压缩)试验测得;强度参数F12由试验获得双向强度后计算得到。

边界元程序计算过程中，若中心试验区的纵向和横向平均应力使准则方程左边大于等于1，则判定十字型试样断裂。

3 实验验证

3．1 基本力学性能测试

在双向拉伸试验之前，对交织玻璃纤维增强复合材料进行基本力学性能测试，从而获得交织玻璃纤维增强复合材料的工程弹性常数和纵、横向拉压强度，所得材料特性见表1。本文研究的复合材料在纵、横向具有相同的力学性能，增强相为交织玻璃纤维织物，基体为WSR618型环氧树脂。

表1 材料特性Table 1 Material properties

3．2 试验结果与分析

双向拉伸试验在SDS100电液伺服动静试验机上进行。主要进行4个载荷比(f=纵向载荷∶横向载荷=1∶1，2∶1，3∶1，4∶1)的双向拉伸试验，试验采用位移控制方式，按f×0．5mm/min的加载速率加载。

同时，对十字型试样的1/4模型，建立了有限元分析模型，获得其有限元分析结果。表2给出了边界元模型与有限元模型的比较。

表2 边界元与有限元分析模型的比较Table 2 Comparison for the models of BEM and FEM

由表2可见，针对同一个分析模型，边界元法在单元数目的划分上要远少于有限元法。因此，其模型的自由度数目也存在较大悬殊，边界元法求解方程数目明显较少，从而节约占机内存及计算时间。由此可见，边界元法在计算效率上比有限元法更具优势。

交织玻璃纤维增强复合材料的双向拉伸纵向应力-应变曲线如图6所示。从图6中可看出，不同载荷比下，材料的双向拉伸应力、应变保持着线性关系。边界元法、有限元法计算结果与试验结果趋势一致，且较为接近。说明2种数值方法的模拟结果都是比较可信的。因此，可利用边界元法，从理论上分析复合材料双向拉伸力学性能。

图6 材料双向拉伸应力-应变曲线(纵向)Fig．6 Stress-strain curve of the material under biaxial tensile(longitudinal direction)

交织玻璃纤维增强复合材料不同载荷比的拉伸强度结果比较见表3。分析表3中数据可知，十字型试样边界元模型与有限元模型计算所得的双向拉伸强度结果较接近;与试验值比较，不同载荷比下2种计算方法的误差范围分别为5．9% ～6．8%和6．4% ～7．3%，且均为正误差。可认为2种数值方法在计算精度上相当，2种方法的计算值均比试验值偏大。误差来源可能有2种:一是实际试样存在一定的缺陷和细微损伤，造成拉伸强度的降低;二是理论分析模型与实际情况不完全吻合。

同时，由表3中结果可见，交织玻璃纤维增强复合材料的双向拉伸行为存在明显的双向弱化现象:在载荷比为1∶1的加载条件下，材料的双向拉伸强度(纵向强度)仅为单向拉伸强度的60．5%;载荷比为2∶1时，双向拉伸强度为单向拉伸强度的71．5%;载荷比为3∶1和4∶1时，双向拉伸强度分别为单向拉伸强度的77．5%和81．2%。由此可见，纵、横向载荷比越小，该材料的双向弱化效应越明显，双向加载为等双拉时，双向拉伸强度最小，材料抵抗双向拉伸破坏的能力最弱。

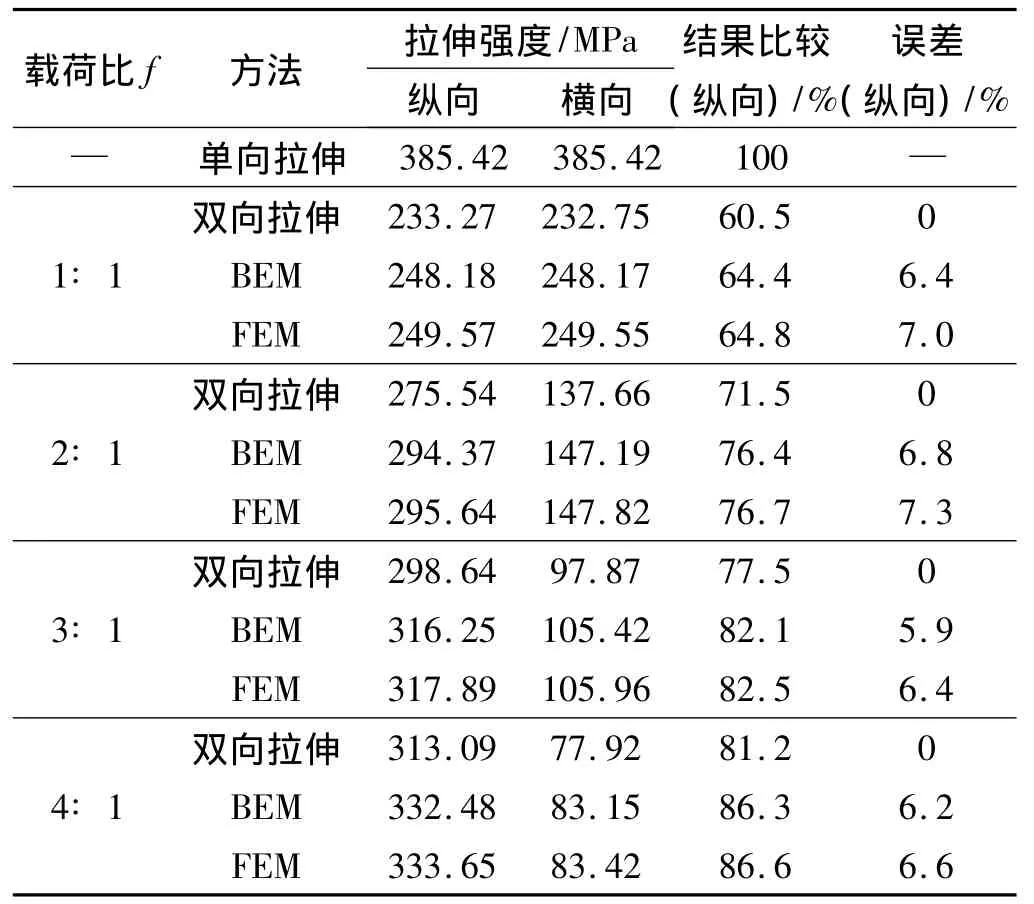
表3 拉伸强度结果及比较Table 3 Results and comparison of tensile strength

十字型试样双向拉伸的破坏形式如图7所示，破坏属于脆性断裂。

由图7可见，不同载荷比下，交织玻璃纤维增强复合材料十字型试样的破坏形式不同∶载荷比为1∶1时，试样沿试验区对角线断裂;载荷比为2∶1和3∶1时，试样裂纹产生及断裂方向与试验区对角线约成10°～15°夹角;载荷比为4∶1时，试样出现明显的分层破坏，且分层方向偏向于载荷大的加载方向。

4 结论

(1)建立了交织玻璃纤维增强复合材料双向拉伸的边界元理论分析模型，理论分析结果与试验结果具有较好的一致性。因此，可利用边界元法，从理论上分析该类复合材料的双向拉伸性能。

图7 十字型试样破坏形貌Fig．7 Fracture morphology of cruciform specimen

(2)在计算交织玻璃纤维增强复合材料双向拉伸强度时，边界元法在计算效率上优于有限元法，计算精度上两者相当;同时，2种方法的计算值均比试验值偏大。

(3)交织玻璃纤维增强复合材料的双向拉伸强度，与其单向拉伸强度相比，具有明显的双向弱化效应。纵、横向载荷比越小，材料的双向弱化现象越明显，等双拉时，材料的双向拉伸强度(纵向强度)仅为单向拉伸强度的60．5%。

(4)不同载荷比下，交织玻璃纤维增强复合材料双向拉伸的破坏形式有所不同，主要表现为试验区纤维断裂方向的不同，载荷比为4∶1时出现了分层破坏。

［1］ Lin W P，Hu H T．Parametric study on failure of fiber-reinforced composite laminates under biaxial tensile load［J］．Journal of Composite Materials，2002，36(12):1481-1503．

［2］ Smits A，Van Hemelrijck D，Philippidis T P，et al．Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates［J］．Composites Science and Technology，2006，66(7-8):964-975．

［3］ Makris A，Vandenbergh T，Ramault C，et al．Shape optimisation of a biaxially loaded cruciform specimen［J］．Polymer Testing，2010，29(2):216-223．

［4］ Serna Moreno M C，López Cela J J．Failure envelope under biaxial tensile loading for chopped glass-reinforced polyester composites［J］．Composites Science and Technology，2011，72(1):91-96．

［5］ Liu Y J．A new fast multipole boundary element method for solving large-scale two-dimensionalelastostatic problems［J］．International Journal Numerical Methods in Engineering，2006，65(6):863-881．

［6］ 陈龙，朱兴一．求解具有弱界面的复合材料有效性能的近似模型与边界元法［J］．复合材料学报，2013，30(2):137-143．

［7］ Lachat J C，Watson J O．Effective numerical treatment of boundary integral equations:A formulation for three‐dimensional elastostatics［J］．International Journal for Numerical Methods in Engineering，1976，10(5):991-1005．

［8］ Pineda León E，Samayoa Ochoa D，Rodríguez-Castellanos A，et al．Creeping analysis with variable temperature applying the boundary element method［J］．Engineering Analysis with Boundary Elements，2012，36(12):1715-1720．

［9］ 刘云忠，雷海峰．正交各向异性复合材料中裂纹问题的边界元法分析［J］．固体火箭技术，1995，18(2):52-61．

［10］ 刘云忠．边界元法计算厚板表面裂纹问题的应力强度因子［J］．固体火箭技术，1996，19(3):64-70．

［11］ 商欣萍，储才元．用边界元法分析试样宽度对非织造土工织物拉伸性能的影响［J］．东华大学学报(自然科学版)，2004，30(1):1-5．

［12］ Araújo F C，d＇Azevedo E F，Gray L J．Boundary-element parallel-computing algorithm for the microstructural analysis of general composites［J］．Computers and Structures，2010，88(11):773-784．

［13］ Wang H T，Yao Z H．Large-scale thermal analysis of fiber composites using a line-inclusion model by the fast boundary element method［J］．Engineering Analysis with Boundary Elements，2013，37(2):319-326．

［14］ Fredholm I．Sur une classe d＇équations fonctionnelles［J］．Acta Mathematica，1903，27(1):365-390．

［15］ Rizzo F J，Shippy D J．A method for stress determination in plane anisotropic elastic bodies［J］．Journal of Composite Materials，1970，4(1):36-61．