基于响应面法的喉栓式喷管型面优化设计①

成 沉，鲍福廷，刘 旸，许 昊

(西北工业大学航天学院，西安 710072)

0 引言

为提高导弹的机动性与灵活性，使得系统满足多任务需求，作为动力装置的固体火箭发动机要具备更强的推力调节能力。在喷管中嵌入一根喉栓，就能在不改变传统固体火箭发动机结构形式情况下，实现推力大小的调节［1－3］。这种推力调节技术因其推力调节比大，理论上能实现无级调节而受到越来越多的关注。

喷管优化设计是喉栓式固体火箭发动机设计中的一个重要方面。由于在喷管中嵌入的喉栓会扰乱传统喷管中的气流路径，使喷管扩张段产生复杂的激波系，甚至引发流动分离等现象，造成比冲损失。所以，喉栓式喷管的优化设计需综合考虑喉栓的型面与喷管型面的相互作用，减小因喉栓插入而引起的比冲损失。

本文通过CFD模拟对喉栓式喷管的喷管型面及喉栓型面进行综合气动优化设计，探寻两者的设计参数对比冲损失的影响，为喉栓式喷管的设计提供参考。由于CFD本身计算量较大，若直接进行优化必须进行大范围的搜索，需消耗巨大的计算量。本文采用响应面法，在设计空间内对有限的设计试验点进行CFD计算，并在此基础上建立响应面模型，再结合序列二次规划法(NLPQL)，对喷管型面及喉栓型面进行综合气动优化设计。结果表明，影响比冲效率的因素主要为喷管的设计参数，在进行喉栓式喷管的优化设计时，喷管部分完全可采用传统喷管的优化设计方法，再针对喉栓进行匹配性优化。应用响应面法，能以相对较小的计算量进行快速优化设计，满足工程优化需求，提高工程优化效率。

1 CFD模型

1．1 数学模型

采用可压缩流动的二维轴对称守恒型N-S方程。对流项采用二阶迎风格式进行离散，粘性项按照中心差分格式进行离散。湍流模型采用RNG k-ε模型，增强壁面函数。

1．2 边界条件

边界处理是流场数值模拟的重要环节之一，当喉栓从完全打开位置向着发动机喉部运动时，喉部面积减小，燃烧室压力升高，发动机入口质量流率随燃烧室压力升高而增加。因此，入口边界条件定义为自适应的质量入口，在计算过程中读入发动机燃烧室压力，自动调整入口质量流率，使其满足药柱的燃速变化规律［3］。单位面积质量流率为

式中 Ab为药柱截面积;Ain为喷管入口面积;ρp为推进剂密度;pc为燃烧室压强;n为燃速指数;a为燃速系数。

发动机喷管出口面上为超音速出口，不需给定任何边界条件，全部气流参数二阶外推即可。

2 响应面法

响应面法是试验设计与数理统计相结合的优化方法，当实验结果与已知参数间的函数关系为隐式时，在试验测量、经验公式或数值分析的基础上，对指定的设计点集合进行连续的试验，可设计实验结果与参变量间的函数关系，并求得参变量的系数，最终建立响应与参变量间的函数关系，在设计空间构造测定量的全局逼近。响应面方法计算简单，因而可仅采用简单的代数形式，依靠目标函数本身的性质确定最优解。通过回归模型的选择，可拟合复杂的响应关系，具有良好的鲁棒性［5］。本文用设计试验点的CFD数值计算结果替代实验结果生成响应面，可大大减少寻求最优解的优化计算次数。

2．1 响应面初始样本点选取方法

几乎所有的基于响应面的优化算法，第一步就是构造初始响应面，而初始响应面构造的首要问题就是初始样本点的选取，科学合理的样本点在样本空间的分布应是均匀的。本文采用中心复合实验设计(CCD)，生成初始试验样本点。CCD的主要特点是可评估因素的非线性影响。

2．2 响应面回归模型

选择适合的响应面回归模型是至关重要的。这关系到响应面模型是否能真实反映目标函数与设计变量之间的关系。

常用的响应面模型有多项式(polynomial regression surrogate，PRS)、径向基函数 (radial basis functions，RBF)、支持向量回归(support vector regression，SVR)、多元自适应回归样条(multivariate adaptive regression spline，MARS)以及 Kriging等。本文选择多项式模型及Kriging模型分别生成响应面，并进行了对比分析。

多项式模型:通常选择一阶多项式为响应面模型，但一阶模型很难反映真实的响应情况;而选择大于二阶的多项式虽然有较高的拟合精度，但它由于包含较多的项，需付出较大的计算代价，尤其是在多变量情况下，拟合响应面要花费的计算时间将是无法承受的。对于气动优化问题，相对来说二阶模型形式比较灵活，对真实响应近似程度较好。本文基于CFD的计算结果，采用完全二次多项式构造响应面模型。其一般公式为

式中 k为变量个数;ε为统计误差。

Kriging模型:Kriging方法是一种通过已知点来预测未知观察点的一种插值方法。Kriging方法利用方差的变化来表达空间的变化，且可保证由空间分布得到的预测值的误差最小。

由于Kriging方法生成的响应面经过所有的试验样本点，无法直接通过试验样本点与响应面计算值的拟合程度来评估响应面模型有效性。文中采取额外随机抽取测试样本点的方法，用测试样本点与响应面计算值的拟合程度来更好地评估响应面模型有效性。

2．4 优化算法

本文采用序列二次规划法在响应面上进行寻优。这种算法假设目标函数是连续可微的。基本思想是将目标函数以二阶拉氏方程展开，并把约束条件线性化，使其转化为一个二次规划问题。二阶方程通过Quasi-Newton公式得到了改进，而且加入了直线搜索，提高了算法的稳定性。

3 优化算例及结果分析

3．1 优化模型

本文优化的喷管型面采用双圆弧法设计，而喉栓型面为头部带小圆弧的圆锥形，喷管及喉栓构型如图1所示。一般设计喉栓式喷管时，要满足喷管长度限制的要求。为了满足发动机的内弹道要求，还需保证喷管的最大、最小等效喉部截面积(喉栓插入喷管中所形成的最小截面面积)一定。所以，本文在喷管长度和喉栓直径一定、且保证等效喉部面积恒定的条件下，为了达到比冲损失最小目标，选择了图1所示的设计参数，对喷管型面及喉栓头部型面进行了优化。

图1 喷管及喉栓型面构型图Fig．1 The contour of the pintle nozzle

其中，喷管设计参数为喷管收敛段与水平方向的夹角α，喉部小圆弧半径R1，扩张段大圆弧半径R2，喷管出口半径Re;喉栓设计参数为头部圆锥半角θ，头部小圆弧半径r。

本文以与喉栓式喷管等效喉部截面积相等的最优标准喷管(无喉栓的传统喷管)的比冲为标准，评价喉栓式喷管的比冲损失。比冲损失定义如下:

式中 Isp为喉栓式喷管的比冲;Iss为最优标准喷管的比冲。

最优标准喷管的比冲是基于响应面法对相同的喷管设计参数，在同样条件下，对标准喷管进行优化后计算得到的。

3．2 结果及分析

基于CCD方法，生成了45个初始试验样本点(DOE points)，并随机抽取了38个测试样本点(Verification points)进行CFD计算。分别用多项式模型及Kriging模型生成响应面。图2和图3分别显示了2种模型的拟合效果。图中横坐标为样本点CFD计算值，纵坐标为响应面预测值;方块表示初始试验样本点，圆圈表示测试点，样本点越接近中线，说明拟合程度越好。可看出，对于测试样本点，2种模型的预测效果都不错，多项式模型的均方根误差(Root Mean Square Error)RMSE=0．009%，Kriging 模型的 RMSE=0．005%。均方根误差RMSE(%)的定义如下:

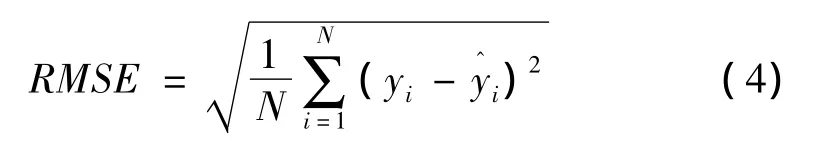
式中 yi为CFD计算的准确值;y^i为响应面模型预测值;N为评估测试点数。

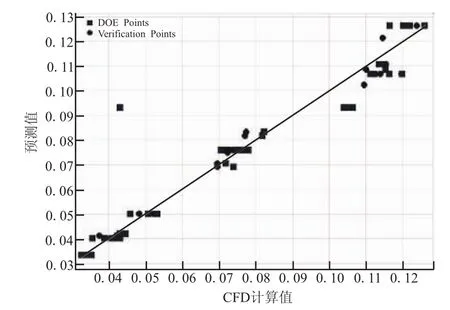
图2 多项式模型拟合图Fig．2 The response surface created by the PRS

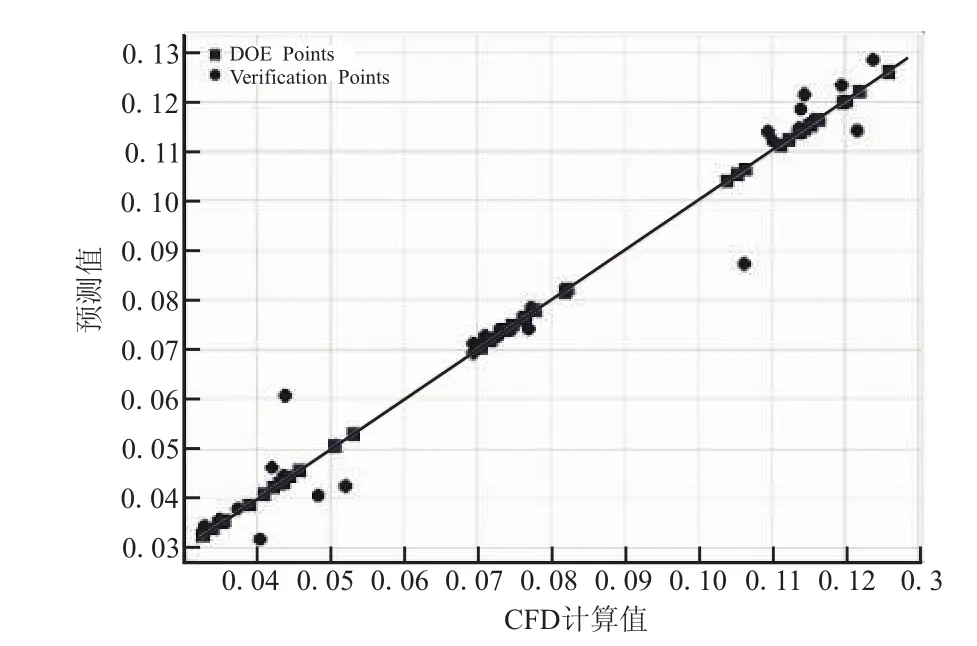
图3 Kriging模型拟合图Fig．3 The response surface created by the Kriging

可见，2种模型的精度都足以满足要求，而Kriging模型初始试验样本点全部通过响应面，多项式模型中存在偏差较大的初始试验样本点。相比而言，Kriging模型表现较好，较适用于喉栓式喷管的优化设计问题。本文优化时，选择Kriging模型。用序列二次规划法在Kriging响应面上优化的结果如表1所示。在响应面上寻优的结果，使比冲损失从9．01%降到了4．52%。对此优化点进行CFD计算，得到的比冲损失为4．52%。响应面误差为1．6%，精度满足要求。对优化点整化之后，再进行 CFD计算，得到最终的比冲损失为4．50%。图4和图5是优化前后流场的对比。可看出，优化后喉栓头部的亚音速区明显减小，从喉栓头部延伸出的斜激波强度减弱。从图6可看出，喷管出口处的径向速度明显减小。由于只有轴向速度对比冲有贡献，而径向速度越大，比冲损失越大。优化后，喉栓对流场的扰动作用减弱，流动损失自然减小了。

表1 优化结果(Kriging模型)Table 1 Optimization results(Kriging model)

图4 优化前流场马赫数云图Fig．4 Mach number contour before the optimization

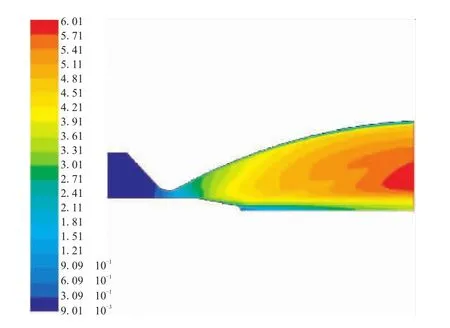
图5 优化后流场马赫数云图Fig．5 Mach number contour after the optimization

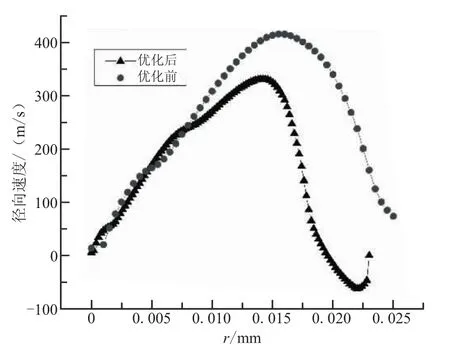
图6 喷管出口径向速度Fig．6 The radial velocity of the outlet

3．3 关键参数分析

各设计参数的敏感性如图7所示。其中，喷管设计参数扩张段大圆弧半径R2、喷管出口半径Re及喉栓设计参数头部圆锥半角θ对比冲损失的影响较大。

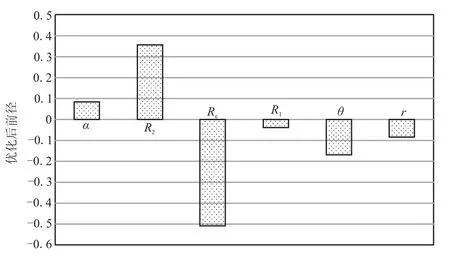
图7 参数敏感性Fig．7 The sensitivity of parameters

以优化点为基础，再进一步针对这几个参数进行单独的优化，得到的响应面如图8所示。可看出，R2小于140 mm时，比冲损失较小;超过140 mm时，比冲损失会急剧增加。比冲损失随Re的增大几乎呈线性减小，在允许范围内，Re越大越好。θ对比冲损失的影响相对前两个参数较小，小于70°时，随θ的增大，比冲损失增大的较明显;超过70°时，比冲损失几乎不变。

再对这几个参数进行单独寻优，组成新的优化点，比冲损失下降为3．63%。优化点为 α=44°，R1=3 mm，R2=120 mm，Re=26 mm ，θ=10°，r=1．3 mm。

3．4 优化方式改进

总体而言，喷管设计参数比喉栓设计参数的影响要明显一些，而喉栓的设计参数对比冲损失的影响不是很大，影响比冲效率的主要因素还是喷管的设计参数。

图8 关键参数响应面Fig．8 The response surface of the key parameters

基于上述分析，改变优化方式，先对喷管进行优化，再对喉栓进行优化。这样试验点从45个，减小到了34个，减小了计算量。优化结果与综合优化结果的对比如表2所示，分开优化得到的优化结果与综合优化的差别不大，这种优化方式能在达到同样优化效果的前提下，减小计算量。

在进行喉栓式喷管的优化设计时，喷管部分完全可采用传统喷管的优化设计方法，再针对喉栓进行匹配性优化。

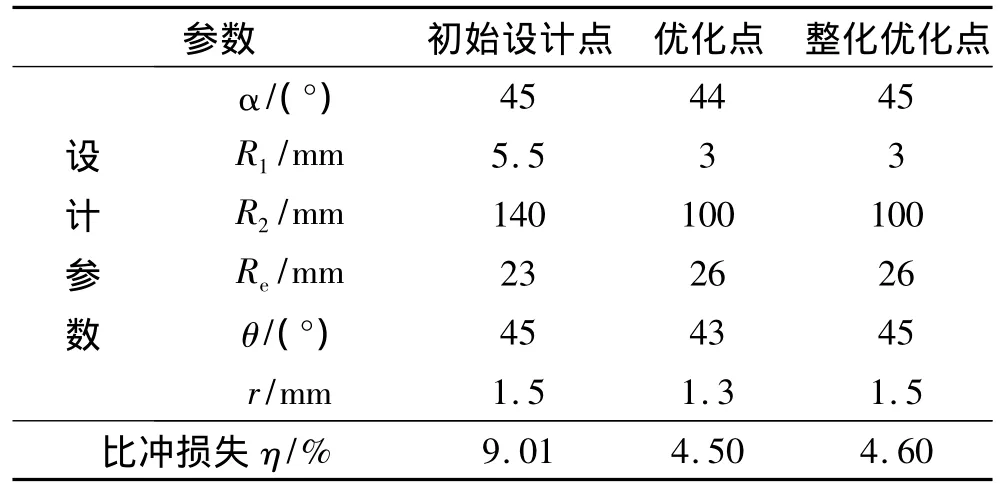
表2 改进的优化结果Table 2 Improving optimization results

4 结论

(1)喉栓式喷管的型面优化问题需综合考虑喉栓型面和喷管型面的相互影响，以得到最优气动型面。

(2)对于文中的问题，Kriging模型比完全二阶多项式模型拟合程度高，预测能力好，适用于喉栓式喷管的优化设计。

(3)基于响应面法进行喉栓式喷管的型面优化设计，计算量相对较小，计算结果的精度和可靠度相对较高，可快速进行气动优化设计，具有一定的工程实用价值。

(4)影响比冲效率的因素主要为喷管的设计参数，在进行喉栓式喷管的优化设计时，喷管部分完全可采用传统喷管的优化设计方法，再针对喉栓进行匹配性优化。

［1］ 张淑慧，胡波，孟雅桃．推力可控固体火箭发动机应用及发展［J］．固体火箭技术，2002，25(4)．

［2］ Randall Smith-kent，Hai-tien Loh，Pawel Chwalowski．Analytical contouring of pintle nozzle exit cone using computational fluid dynamics［R］．AIAA 1995-2877．

［3］ 李娟，李江．喉栓式固体火箭发动机喷管性能影响研究［J］．弹箭与制导学报，2007，27(3):154-160．

［4］ 邹林君．基于Kriging模型的全局优化方法研究［D］．武汉:华中科技大学，2011．

［5］ 熊俊涛．基于响应面方法的气动优化设计［D］．西安:西北工业大学，2005．

［6］ 王筱蓉，周长省，鞠玉涛，等．固体火箭发动机特型喷管的型面设计［J］．弹道学报，2008，20(4):77-80．