改进的螺栓连接结构建模方法及其在导弹设计中的应用①
2014-01-16王晓慧樊思思李人杰夏人伟
王晓慧,樊思思,李人杰,夏人伟
(北京航空航天大学宇航学院,北京 100191)
0 引言
导弹舱体以舱段为单位,通过连接结构将各舱段连接装配,连接结构在导弹飞行过程中承受一定强度的飞动升力和重力载荷作用。舱段连接形式的选择,是战术导弹设计中的一个重要课题。目前,国内外常用的连接形式主要有轴向盘式连接和径向螺栓连接。轴向盘式连接承载能力强,连接可靠,但结构尺寸较大,装卸不方便。径向螺栓连接则能弥补以上缺点,其形式简单,结构轻便,且装配和加工都较容易[1]。
在导弹舱段径向连接结构的有限元建模中,舱段套接配合面大、螺栓尺寸小而数目较多,为保证分析精度,在尺寸相对较细小的螺栓及螺孔区域的有限元单元细化上需要很大的计算量,导致结构单元数目庞大,计算效率低下。通常在有限元建模分析时会利用导弹舱段的轴对称特性,仅以单个螺栓区域为研究对象[2-4],但该方法只适用于载荷轴对称的情况,无法应用于其他载荷工况下的导弹结构分析问题。本文提出一种求解效率高、适用性强的舱段连接结构有限元建模方法,以便高效地实现一般载荷工况下的导弹结构分析。
本文基于非线性有限元分析方法,对存在接触、摩擦和预紧等非线性因素的导弹舱段径向连接结构进行建模方法研究,研究工作基于连接结构形式和螺栓预紧力施加方法两方面展开,通过组合得到4种连接结构有限元建模方法,通过平板连接结构算例,验证了4种方法的有效性。在此基础上,通过对某型导弹舱体径向连接结构算例的仿真研究,优选出一种求解效率高、适用性强的导弹舱段径向螺栓连接结构有限元建模方法。通过本文的研究,可实现导弹舱段径向连接结构设计的高效性,为概念设计阶段的导弹舱体设计提供依据,并为进一步的导弹结构优化设计提供技术支持[5]。
1 接触问题有限元法
接触约束算法将接触问题描述为求解区域内的位移场,使得系统势能在接触边界条件约束下达到最小,即
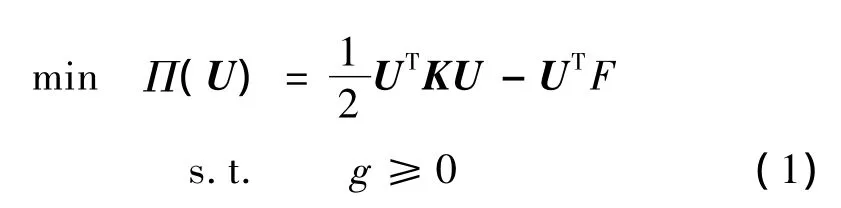
式中 K为系统刚度矩阵;F为接触力;g为间隙函数。
接触约束算法就是通过对接触边界约束条件的适当处理,将式(1)所示的约束优化问题转化为无约束优化问题。Lagrange乘子法是解决小变形、小滑移接触问题最常采用的转化方法。Lagrange乘子法通过引入乘子λ,定义修正的系统总势能为:
一般地,可将g对位移U作Taylor展开
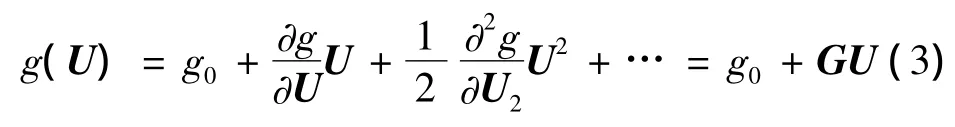
将式(3)代入式(2)后,对U和λ求变分,可得系统代数控制方程为
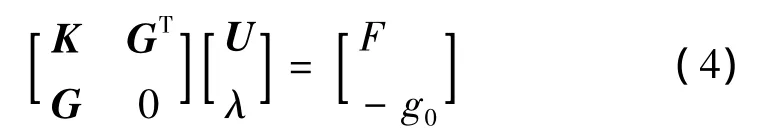
使用Lagrange乘子法需要特殊的界面单元来描述接触,以使接触条件可精确满足,进而形成控制方程,并采用非线性迭代方法求解[6-7]。
基于以上理论,对连接结构进行带接触条件的预紧力模拟有限元建模方法研究,主要包括连接结构的建模方法和螺栓预紧力的施加方法。
2 不同形式的连接结构建模方法
2.1 完全实体单元+接触条件建模方法
完全实体单元+接触条件建模方法是基于实体结构来建立模型(图1),对结构的保真程度最高。同时,这种建模方法可考虑所有部件间的接触,分析各个部件间的接触应力分布,特别是螺栓和被连接件之间的接触应力分布。但为了得到较精确的结果,需要在模型的建立上投入大量的时间;同时,由于接触对较多,计算效率较低(简称为实体单元建模方法)[2-4]。
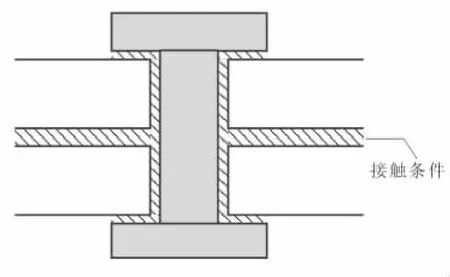
图1 完全实体单元+接触条件建模方法示意图Fig.1 Method of solid element with contact
2.2 梁单元配合MPC+接触条件建模方法
梁单元配合多点约束(Multi-point Constraints,MPC)+接触条件建模方法将螺栓用梁单元代替,再将梁单元两端用MPC与被连接件螺孔两端相连(图2)。这种建模方法可减少螺栓单元数目和接触对数目,计算效率会得到很大提高。但由于未定义梁单元与被连接件间的接触关系,这种方法不能求解被连接件与连接件之间的接触应力分布[8](简称为梁单元建模方法)。
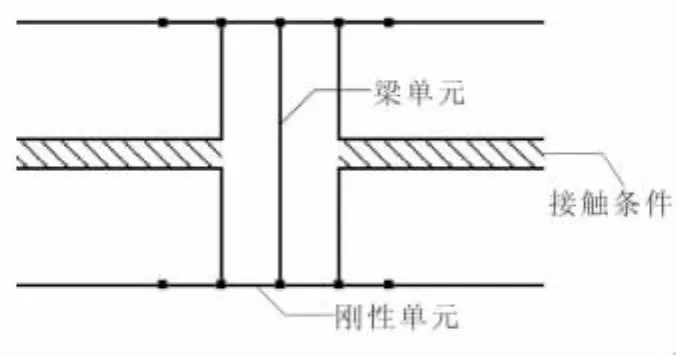
图2 梁单元配合MPC+接触条件建模方法示意图Fig.2 Method of beam element added MPC with contact
2.3 刚性连接+接触条件建模方法
刚性连接+接触条件建模方法用刚性单元将被连接件连接起来(图3),但由于是使用刚性连接来模拟螺栓连接,因此仅对刚性较强的螺栓模拟程度较高;同时,这种方法不便施加预紧力。
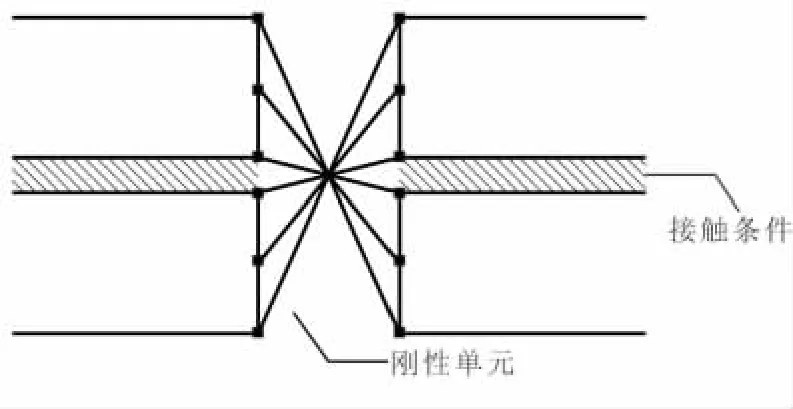
图3 刚性连接+接触条件建模方法示意图Fig.3 Method of rigid connection with contact
2.4 一体化建模方法
一体化建模方法是直接将螺栓和被连接件建为一体(图4),这种建模方法的模型简单,忽略螺栓和螺孔,易进行网格划分,但无法求解被连接部件间的接触压力分布,也无法施加预紧力,适用于对大型结构小范围局部连接的处理[5]。
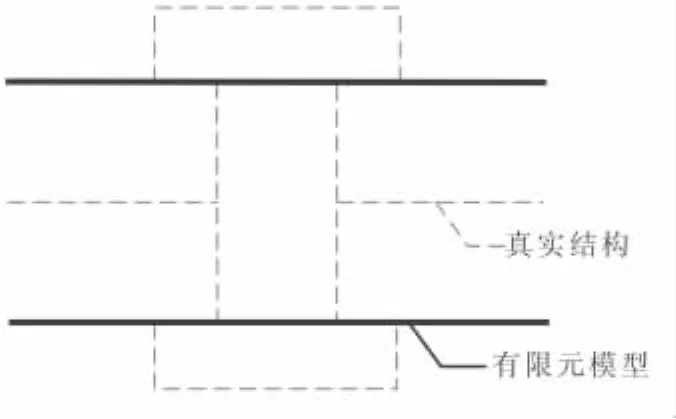
图4 一体化建模方法示意图Fig.4 Method of all-in-one
3 螺栓预紧力施加方法
3.1 直接施加法
直接施加预紧力的方法,其原理如图5所示,螺杆有限元网格被分割成两部分,裂口两边互相对应的节点通过多点约束方式连接起来,并在分离的两部分间产生间隙或重叠。分离两部分的运动被限制在产生间隙或重叠的方向上,交叠将使两部分产生拉(预)应力,间隙则引起压应力。
3.2 等效外载法
通过在被连接件两端施加一对压力外载荷来模拟预紧力的效果。压力外载值将通过刚度分配原理给出,以螺栓连接结构为例,其刚度分配方法如下:

式中 Q为被连接件两端施加的压力外载;Qb为螺栓承受的压力;Qp为被连接件承受的压力(预紧力)。
根据变形协调条件确定外载:

式中 Δlb为螺栓轴向变形;Δlm为被连接件沿螺栓轴向变形;Cb为螺栓刚度;Cm为被连接件刚度[9]。
在这种施加方法中,螺栓受压,与真实情况下螺栓受拉不同。因此,分析得到的螺栓受力不能反映真实工程中螺栓的受力,只能模拟被连接件的受力情况。
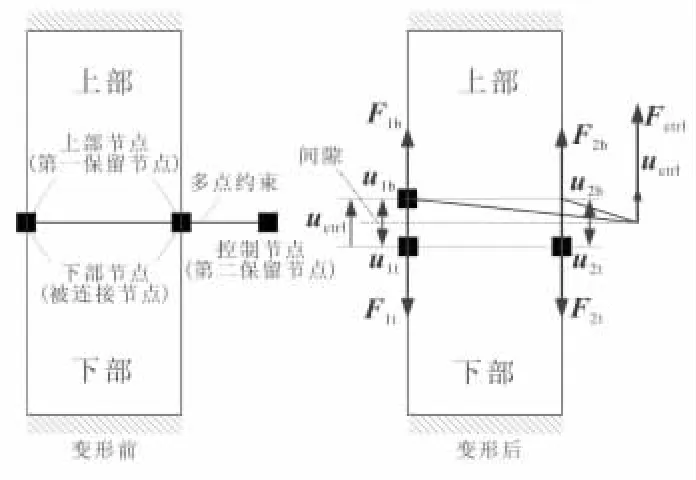
图5 直接施加预紧力原理示意图Fig.5 Method to add preload
4 建模方法对比研究
在本章中,将对以上方法进行对比研究,由于刚性连接+接触条件和一体化建模方法都省去了螺钉,故无法进行预紧力模拟。将其他2种连接结构形式建模方法与2种预紧力施加方法进行组合,得到4种组合建模方法,通过一个基础平板连接结构对4种组合方法进行对比研究,评价各方法的优劣性选择出一种合适的方法,用于导弹舱段径向连接结构中对螺钉的建模。
将2块平板用M8规格的螺栓连接,如图6所示(单位mm)。螺栓施加的预紧力为30 kN,板1左端固定,板2右端平面中心施加载荷,轴向拉力T=1 kN,剪力Q=2 kN,平板表面摩擦系数为0.1。
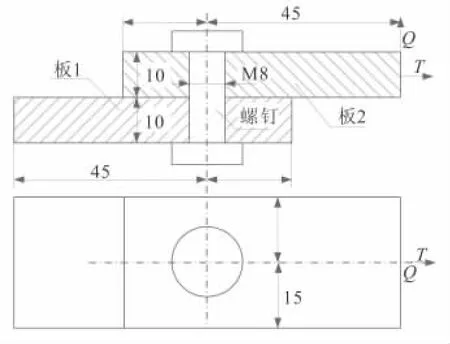
图6 平板连接结构尺寸示意图Fig.6 Detail size of the flat structure
在MSC.Patran有限元软件中,对结构进行建模。其中,采用实体单元建模方法得到的有限元模型如图7(a)所示;采用梁单元建模方法得到的有限元模型如图7(b)所示。
在4种组合方法下,分别进行结构分析,并对比接触力分布,以此作为预紧力作用效果的评价。表1给出平板连接结构在4种方法下各自的最大接触力的数值及其发生位置。表1中,位置中1/3面表示1与3的接触面。其中,1为板1,2为板2,3为螺头,4为螺母。
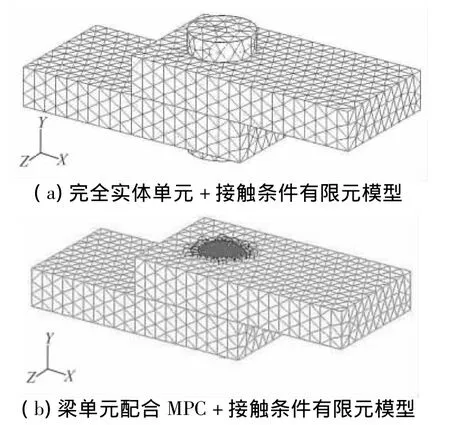
图7 平板连接结构有限元模型Fig.7 Finite element model of the flat structure
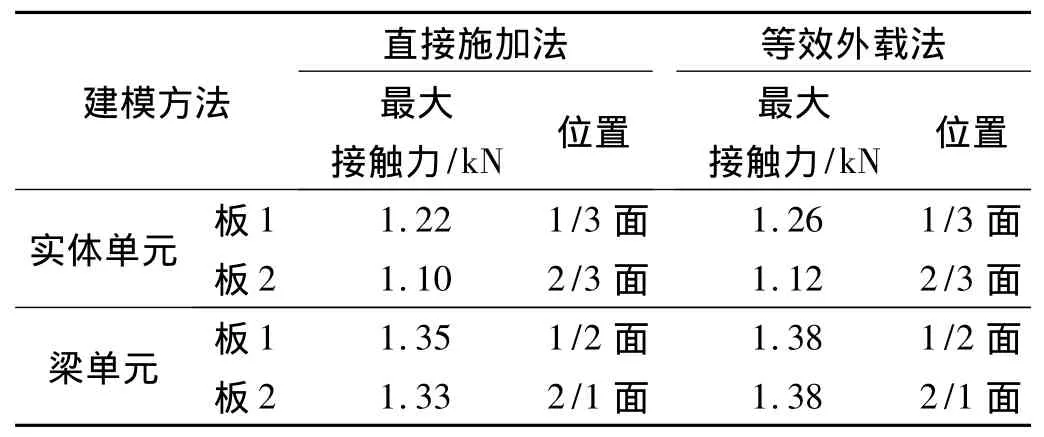
表1 4种组合方法下结构最大接触力对比Table 1 Constrast of maximum contact force between four methods
图8给出实体单元建模方法采用不同预紧力施加方法在1/3面接触力的分布情况。对同一种建模方法,采用不同的预紧力施加方法得到的接触力分布情况基本相同,最大接触力差异约在10%以内。预紧力作用在板件上的效果基本相同。
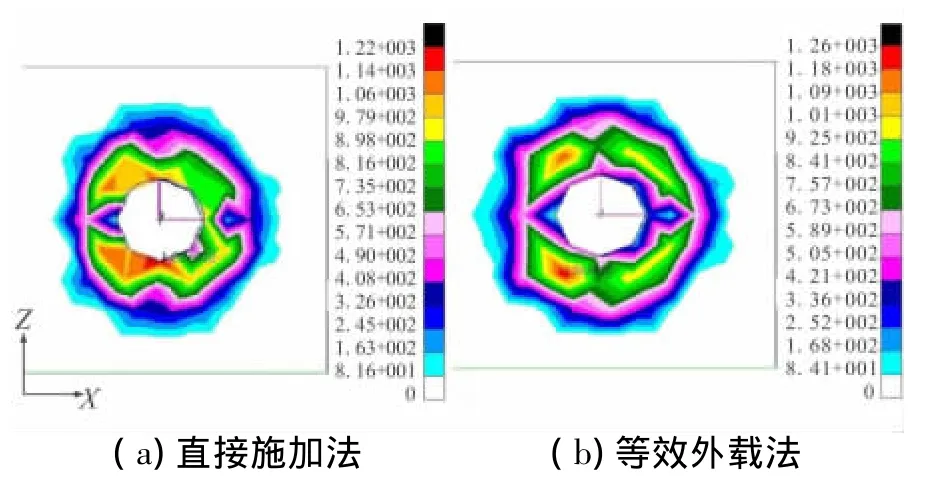
图8 实体单元建模方法板1与螺栓接触面接触力分布Fig.8 Distribution of contact force in 1/3 of solid model
图9给出梁单元建模方法在1/2面接触力的分布情况。对比图8和图9,同一种预紧力施加方法,实体单元建模方法得到的最大接触力发生在1/3面上,而梁单元建模方法由于忽略螺母部分,出现在1/2面上。
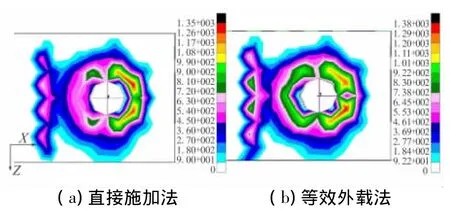
图9 梁单元建模方法板1与板2接触面接触力分布Fig.9 Distribution of contact force in 1/2 of beam model
图10给出实体单元建模方法在1/2面接触力的分布情况。图9和图10对比,梁单元建模方法忽略螺母,预紧力全部通过板1与板2间相互挤压来承担,而实体单元建模方法还可通过板件与螺栓的挤压来承担。因此,在1/2面上的接触力水平是实体单元的1.5倍,也是符合实际情况的。
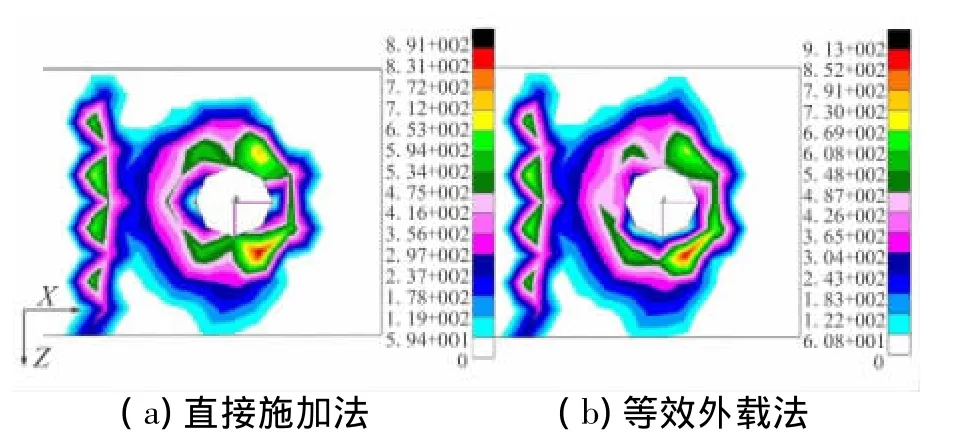
图10 实体单元建模方法板1与板2接触面接触力分布Fig.10 Distribution of contact force in 1/2 of solid model
通过平板连接结构,可验证直接施加法与等效外载法在预紧力作用效果的等效性,以及梁单元建模方法与实体单元建模方法间的等效性。
但采用实体单元建模方法对螺栓进行建模,结构分析耗时约为梁单元建模方法的5倍,计算效率较低。采用等效外载法需要通过刚度分配来确定等效外载值,存在着刚度确定难。确定准确性低的缺点,在复杂连接结构中将突显出来。
5 某型导弹舱段径向螺栓连接结构算例
通过理论及实践的分析,有4种方法适用于螺钉预紧的仿真,在处理结果上它们之间具有等价性,但彼此又存在着一定的优劣差异。其中,梁单元建模方法结合直接施加法施加预紧力是最适合于复杂连接结构的建模方法。下面将针对某型导弹舱段径向螺栓连接结构来进一步验证这一结论。
某型直径为600 mm的2个导弹舱段套接配合在一起,周向通过24个径向M8的螺栓进行连接,结构各具体参数详见图11(单位mm)。螺栓施加的预紧力为30 kN,外载荷作用在舱段2的右端轴心,弯矩M=90 kN·m,轴向拉力T=30 kN,剪力Q=60 kN,舱段1左端固定,舱段表面摩擦系数定义为0.1。
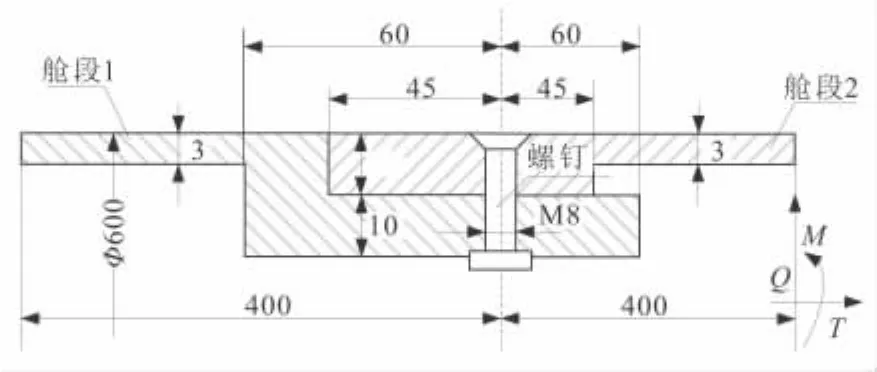
图11 导弹结构尺寸示意图Fig.11 Detail size of the missile structure
在MSC.Patran有限元软件中,对结构进行建模,采用实体单元建模方法得到的模型问题规模太大无法求解,采用梁单元建模方法得到的有限元模型如图12所示。

图12 导弹结构有限元模型图(局部剖)Fig.12 Finite element model of the missile structure
图13(a)给出了采用直接施加法的导弹舱段连接件接触力分布图,图13(b)为采用等效外载法的导弹舱段连接件接触力分布图。2种预紧力施加方法作用效果基本相同。
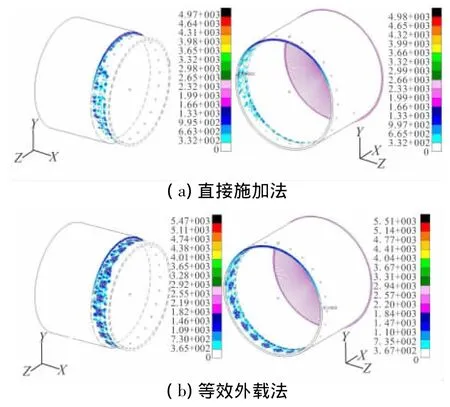
图13 导弹舱段接触力分布图Fig.13 Distribution of the contact force in two cabins
表2给出了基于梁单元模型的2种预紧力施加方法下结构最大接触力对比。从表2可看出,通过等效外载法施加预紧力得到的最大接触力较大,这主要是由于将导弹舱段等效为圆筒求解刚度[10],而忽略筒径的局部加厚及螺孔,故求得的刚度较实际偏大,导致实际施加在螺栓上的预紧力大于设定的30 kN。
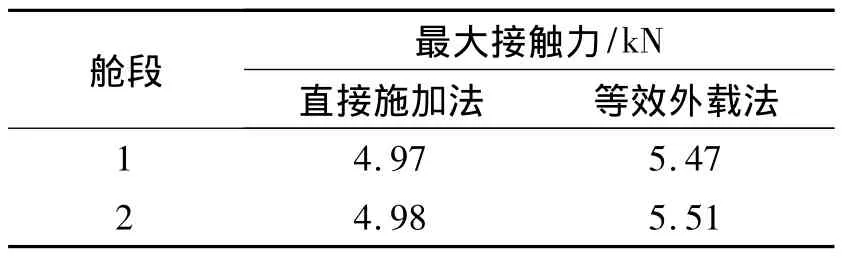
表2 2种预紧力施加方法下结构最大接触力Table 2 Maximum contact force of adding preload in different ways
综上所述,梁单元建模方法配合直接施加法的预紧力施加方法,是一种可实现导弹舱段径向螺栓连接结构高效求解的有限元建模方法。
6 结论
(1)从施加预紧力的作用效果考虑,采取螺栓用梁单元建模实现的方法和螺栓用实体单元建模实现的方法可起到相同的效果,且螺栓用梁单元建模可更好地表达被连接件之间的作用关系,同时很大程度上提高结构分析的计算效率。
(2)利用直接施加法和等效外载法,均可实现预紧力的模拟。其中,直接施加法不存在刚度分配的问题,是一种更准确和方便操作的预紧力施加方法。
(3)通过连接螺栓采取梁单元建模法和预紧力采取直接施加法的综合应用,实现了对某型导弹舱段径向螺栓连接结构的高效建模及分析。本文方法可作为导弹结构在方案设计阶段的理论基础;同时,为进一步的结构优化设计提供了有效的技术支持,在复杂工况下的机械连接结构的有限元建模方法,上具有一定的理论及应用价值。
[1] 余旭东,葛金玉.导弹现代结构设计[M].北京:国防工业出版社,2007:262-270.
[2] Rubin A M.Contact stress of connected axisymmetric cylindrical shells of different length in contact-pressure discontinuity zones[J].Russian Engineering Research,2010,30(1):17-19.
[3] Kozhevnikov V F.Contact interaction of a bolt with hole walls in a double-shear connection[J].Journal of Machinery Manufacture and Reliability,2012,41(1):43-47.
[4] Cho J R,Lee D Y,Yoo W S,et al.Numerical investigation of bolt fitting and fastening forces by elastoplastic finite element analysis[J].The International Journal of Advanced Manufacturing Technology,2013(66):71-81.
[5] 王晓慧,郑海峰,刘昊鹏,等.基于Hyperworks的折叠翼结构优化设计[J].固体火箭技术,2012,35(6):795-798.
[6] 徐超,余绍蓉,郑晓亚,等.机械螺栓法兰连接的有限元力学模型分析比较研究[J].机械设计与制造,2009(6):37-39.
[7] Zang Meng-yan,Gao Wei,Lei Zhou.A contact algorithm for 3D discrete and finite element contact problems based on penalty function method[J].Computational Mechanics,2011,48(5):541-550.
[8] 徐梓雯,那景新,张志远,等.螺栓连接有限元模型的弹性接触研究[J].中国机械工程,2012,23(15):1830-1833.
[9] Nawras Haidar,Salwan Obeed,Mohamed Jawad.Mathematical representation of bolted-joint stiffness:A new suggested model[J].Journal of Mechanical Science and Technology,2011,25(11):2827-2834.
[10] 张婷,陈五一.薄壁筒类零件刚度表述模型的研究[J].航空制造技术,2010(9):7-80.
