基于动网格的喉栓式推力可调喷管内流场数值模拟①

唐金兰，宋慧敏，李进贤，冯喜平

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

喉栓式推力可调喷管能够实现固体火箭发动机的推力连续可调，从而提升了导弹武器的机动性和突防能力，具有强烈的军事需求背景。因此，国外对喉栓式推力可调喷管发动机的相关技术在理论方面、数值模拟、试验研究以及相关的基础学科研究领域都开展了较多的研究［1］。国内对于喉栓式推力可调喷管的相关研究［2］起步较晚，且研究多集中在性能分析与流场的稳态数值模拟方面，基于动网格的喉栓式推力可调喷管内流场的动态特性的研究鲜见报道。

本文利用动网格技术，对喉栓调节运动过程中喷管的内流场进行了数值模拟和分析，分析结果对喉栓式推力可调喷管的实验器设计及实验研究具有一定的指导意义。

1 数理模型与计算方法

1．1 物理模型

由文献［3］的研究结果可知，燃气进入喷管的角度对喷管内流场的影响不大。因此，本文对轴向进气的喉栓式推力可调喷管进行轴对称二维内流场分析，以探讨喉栓调节运动过程对喷管内流场特性的影响。喉栓式可调喷管的物理模型如图1所示。

图1 可调喷管示意图Fig．1 Diagram of pintle-controlled nozzle

式(1)给出了喉栓式推力可调的基本原理。

式中 ρp、C*、a、n分别为固体推进剂的密度、特征速度、燃速系数和压强指数;Ab为推进剂药柱燃面面积;At为发动机喷管喉部面积。

对于选定的推进剂，ρp、C*、a、n可视为常量。假定推进剂药柱等面燃烧，即Ab不变，则At是唯一的变量，只要改变At就可有效地改变燃烧室的压强，从而改变了发动机的推力(F=CFpcAt)。

1．2 数学模型

1．2．1 控制方程

采用N-S方程，将雷诺守恒定律得到的质量、动量和能量守恒方程写成微分形式，就得到了考虑气体粘性和热传导等流体属性的、描述燃气流动的非线性偏微分方程组，式(2)为N-S方程的张量形式:

式中 φ 为通用变量(φ=1，u，v，w，T分别对应连续方程、动量方程和能量方程);Γφ是与φ对应的广义扩散系数;湍流脉动附加项(Γi是与 φ 对应的湍流扩散系数);S为广义源项。

1．2．2 湍流模型

采用RNG k-ε湍流模型，湍流动能k方程和湍流耗散率 ε 方程［5］如下:

湍动能k方程:

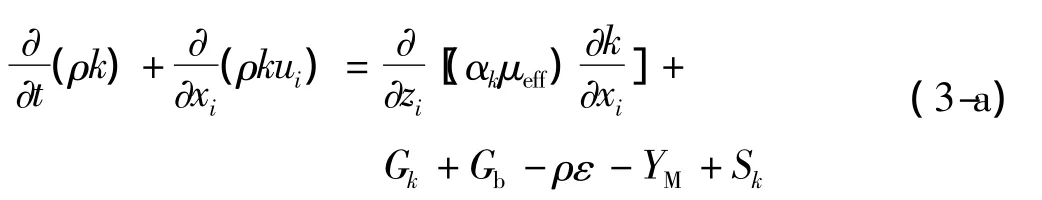
湍流耗散率ε方程:

式中 Gk是由平均速度梯度引起的湍流动能;Gb是由浮力影响引起的湍流动能;YM可压缩湍流脉动膨胀对总的耗散率的响应;C1ε、C2ε、C3ε是常量(一般取 C1ε=1．44，C2ε=1．92，C3ε=0．09);αk、αε是 k、ε 方程的湍流普朗特数(一般取 αk=1．0，αε=1．3)。

1．2．3 动网格技术

采用动网格技术后，计算区域是变化的。所以，在任意的控制体对任意广义标量φ，有积分守恒方程［6］:

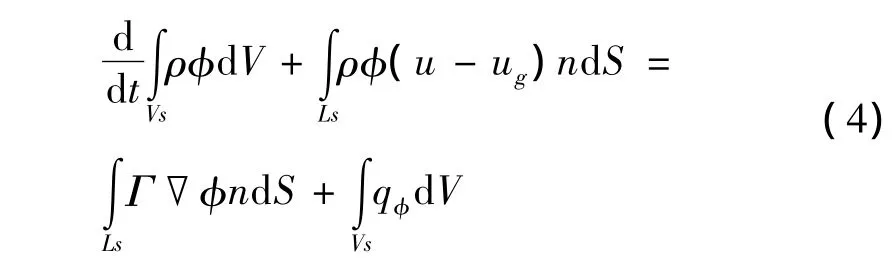
式中 Vs是控制体体积;Ls是控制体的表面边界;u是流体时均速度;ug是动网格边界移动速度;n是表面边界的外法线单位向量;Γ是扩散系数;qφ是源项。

对于喉栓调节运动区域的网格，采用动态层更新方法，即根据相邻运动边界网格层的高度变化，合并或者分割动态网格层，如图2所示。

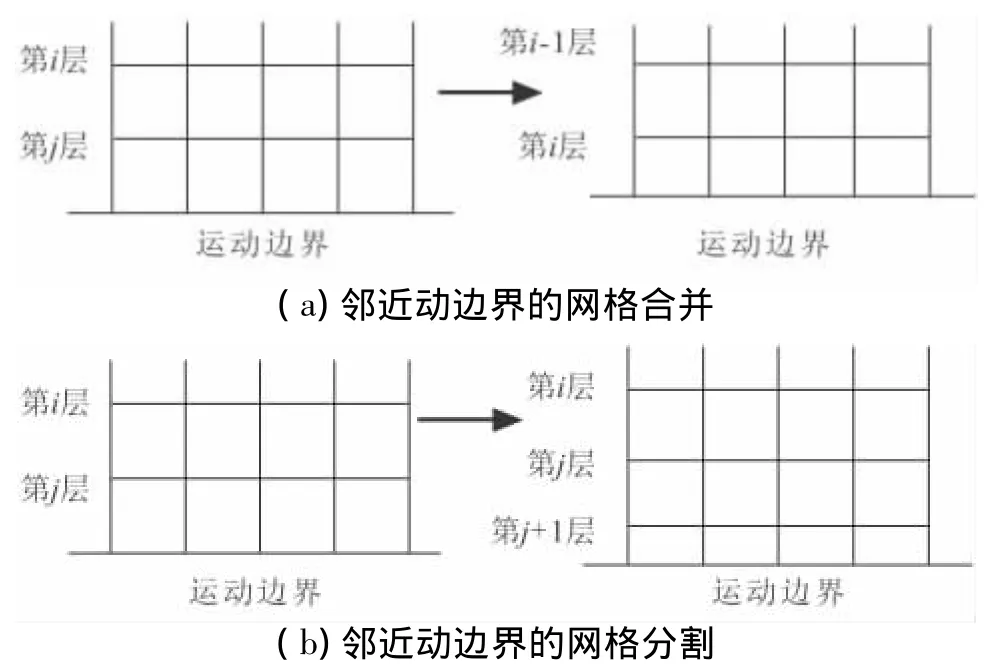
图2 动态网格层的合并与分割Fig．2 Diagram of dynamic layering update by merging and splitting

如果分割网格层，网格单元高度的变化有一临界值:

式中 hmin为网格单元的最小高度;h0为理想网格单元高度;αs为网格层的分割因子。

在满足式(5)的情况下，采用常值高度法(即网格单元分割的结果是产生相同高度的网格)进行网格分割。本文中，喉栓表面是运动边界，而其他部分保持静止。因此，在喉栓表面的运动边界上运用动网格技术。

1．3 初始与边界条件

(1)初始条件。初始压强、初始质量流率、总温分别为2 MPa、0．077 34 kg/s、1 500 K 的条件下的定常计算结果作为本文的初始条件。

(2)入口边界条件。定义为自适应的质量流率入口。通过UDF程序读入燃烧室压力，自动调整入口质量流量，使其满足质量流量变化规律。喉栓从完全打开位置向喷管几何喉部运动时，喷管质量流率的变化由式(6)给出。

式中 n为固体推进剂压强指数;pc、At、m·为喉栓未介入时的燃烧室压强、喷管几何喉部面积和初始质量流率;pc，x、At，x、m·x为喉栓相应调节位置下的燃烧室压强、喷管等效喉部面积和质量流率。

由式(6)可见，只要计算出喉栓运动到某位置时的喷管等效喉部面积，即可得出该位置下相应的质量流率和燃烧室压强。

(3)出口边界条件。定义出口边界压强为101 325 Pa。由于喷管内流场出口为超声速流动，压强出口边界各参数外推得到。

(4)壁面边界。采用无滑移边界条件，近壁区采用标准壁面函数。

(5)对称边界。对称轴上法向速度为零，其他所有流动变量的梯度为零。

1．4 计算分析方法

1．4．1 网格划分

数理模型建立后，计算分析前，应对物理模型进行网格划分［4］。网格划分如图3所示，区域1和区域3采用四边形结构化网格，区域2采用三角形非结构化网格，并进行网格细化，以防止出现由于喉栓的调节运动而可能出现的负网格。

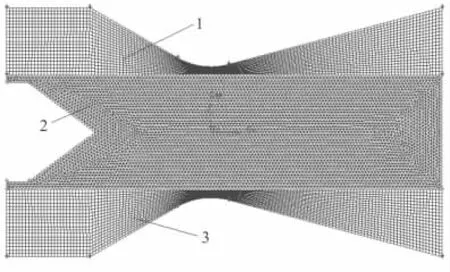
图3 喉栓式推力可调喷管内流场网格划分Fig．3 Meshing of pintle-controlled nozzle flow field

1．4．2 计算分析流程

计算分析流程主要包括流场压强、质量流率等流场参数的更新、流场计算分析、网格更新等几个过程，如图4所示。计算时，需编写喉栓头部运动函数，用函数DEFINE_CG_MOTION定义喉栓头部运动速度。

图4 计算分析流程图Fig．4 Flow chart of CFD program

2 计算结果分析与讨论

2．1 计算结果与分析

图5 给出了 0．1、0．5、1．0 m/s调节速度下，喉栓从未介入到完全介入过程中，喷管入口静压与时间的变化。从图5可见，调节速度越大，调节喉栓所需的时间越短、压强的变化趋势也越快，但在调节的初始位置，调节速度越大，喷管的入口静压就越小(小于初始条件给定的压强值2 MPa)，导致这一现象的原因主要是喉栓的快速运动，使压强建立过程出现了一定的延迟。

图5 入口静压随调节时间的变化关系Fig．5 Inlet static pressure with different regulation time

对推力可调喷管喉栓处于不同调节速度下的内流场进行了动态特性分析，调节速度为1．0 m/s时，3个位置的分析结果如图6所示。

图6 调节喉栓处于不同位置时喷管内的压强和马赫数分布Fig．6 Pressure and Mach number distribution of pintle-controlled at different positions

由图6(a)可见，由于喉栓尚未介入喷管喉部，喉栓对喷管喉部处的内流场几乎没有影响。此时，喷管喉部的燃气膨胀均匀、达到声速，喷管等效喉部面积最大。为50．27 mm2，喷管入口静压最低，为1．8 MPa，喷管出口处的平均马赫数为1．34。

由图6(b)可见，当喉栓处于调节介入的中间阶段时，除等效喉部处外，在喉栓头部尖端附近也形成了一个马赫数为1的小区域。分析该区域产生的原因，是由于在喉栓头部尖端出现了气流分离现象，使气流在喉栓头部尖端区域的压强(约1．61～2 MPa)明显比周围区域的压强(0．79～1．34 MPa)要高，而马赫数则比周围区域略低。由于此时喉栓的调节介入，喷管等效喉部面积减小为27．47 mm2、喷管入口静压上升达到5．35 MPa。因此，喷管出口处的平均马赫数也随之提高到约 2．31。

由图6(c)可见，当喉栓完全介入喷管几何喉部位置，气流明显受到喉栓的影响，而在喉栓头部尖端变化剧烈，并在扩张段中心区域形成了一个受喉栓影响产生的低马赫数区域。喉栓处于完全介入状态。此时，喷管等效喉部面积达到最小为21．99 mm2，喷管入口静压也达到最大为11．29 MPa。因此，喷管出口处的平均马赫数也随之达到最大值2．9。

由图6(b)、(c)可见，随着喉栓调节介入的不断深入，喉栓头部对流场的扰动越来越大，从而使喉栓头部处气流的压强、马赫数与周围流场的差异也越来越大，在完全介入情况下，喉栓头部处的流动分离现象也最明显。同时，由于喉栓调节对流场的扰动，在喉栓头部存在马赫数为1的等值线区域，在该区域产生了斜激波，该激波在喷管扩张段下游发生反射，并随着喉栓的调节深入，该激波及其反射区也向喷管出口移动，燃气经过该斜激波后的压强略有增大。

2．2 喉栓调节速度对流场特性的影响

不同调节速度下，典型的计算结果如表1所示。由表1可知，在不同的喉栓介入状态下，随着喉栓调节速度的增加，喷管入口静压的建立有一定的延迟，需要经过缓冲一段时间才能达到，调节速度越大，压强建立的延迟情况越明显。分析造成这种现象的原因，是由于喉栓调节速度越大，喉栓对流场的扰动越大，压强建立的延迟程度也越大，从而导致的发动机推力的建立延迟情况越明显。

2．3 稳态和非稳态流场特性分析

为便于比较，喉栓调节速度为1．0 m/s、处于不同调节位置时喷管内流场的稳态压强分布如图7所示，典型的数据结果如表2所示。

表1 不同喉栓调节速度仿真结果的对比Table 1 Comparison of simulation results with different speeds

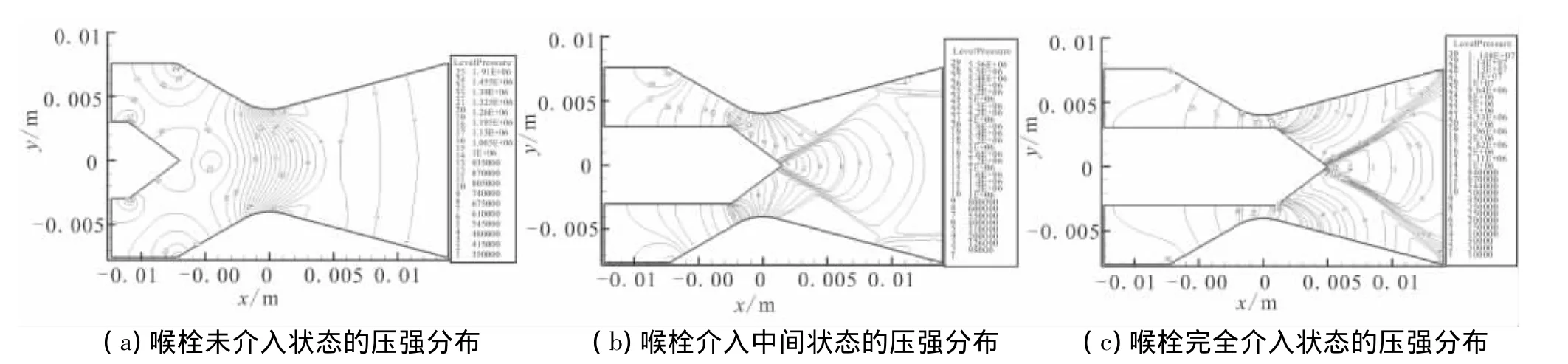
图7 稳态下喉栓处于不同位置的压强变化Fig．7 Pressure distribution of steady condition

表2 稳态和非稳态下的喷管入口静压对比Table 2 Comparison of nozzle inlet pressure between steady and unsteady condition

对比图6、图7及由表2可见，在喉栓完全未介入喷管喉部的情况下，非稳态与稳态的压强分布基本相同;在喉栓调节介入的中间位置和完全介入时，非稳态分析得出的压强明显小于稳态下的压强值。可见，调节速度较低时，喉栓运动对流场造成的干扰较小;随着调节速度的增加，压强的建立会产生延迟现象，而且调节速度越大，压强建立的延迟情况越明显。造成延迟的原因是喉栓调节运动对流场产生扰动，使流场分布还不能及时做出相应变化时，喉栓又运动到了下一节点，从而导致压强的建立存在延迟现象。

由图5可知，喉栓调节速度越快，喉栓调节时间越短。喉栓对流场的扰动时间就越短，在工程实际中，对流场扰动时间越短越好，在对材料、结构等方面不会造成太大影响的前提下，选择一个适中的速度，已达到快速高效的推力可控。而喉栓处于同一位置时，压强的增量随着速度的增大而减小，这就需要对压强的增量进行修正，才能清楚地得出不同喉栓调节速度与压强之间的变化关系，进而实现推力的随机控制。

3 结论

(1)将动网格技术应用到喉栓式推力可调喷管内流场动态特性分析中，可准确地模拟出流场的瞬时变化。

(2)随着喉栓的介入，喉栓头部会产生激波，对喷管流动产生显著影响，且当喉栓完全介入时，影响最大。

(3)喉栓调节速度很小时，流场的分布与稳态下大体相同，随着调节速度增大，流场演化过程有一定的延迟。

(4)在不影响喷管结构前提下，喉栓调节速度越快，对流场造成扰动的时间越短，入口压强响应时间越短，越有利于实现快速的推力可控。

［1］ 李娟，李江，王毅林，等．喉栓式变推力发动机性能研究［J］．固体火箭技术，2007，30(6):505-509．

［2］ 滑利辉，田维平，甘晓松，等．喉栓式推力可调发动机喷管流场数值模拟［J］．固体火箭技术，2008，31(4):344-349．

［3］ 胡博．非同轴喉栓式推力可调喷管内流场及热应力分析［D］．西北工业大学，2013．

［4］ 江帆，陈维平，李元元．基于射流与两相流的射流曝气器研究［J］．流体机械，2005，33(6):18-21．

［5］ 杨建明，吴建华．动网格技术数值模拟挑流冲刷过程［J］．水动力学研究与进展，2001，16(2):156-161．

［6］ Moureau V，Lartigue G，Sommerer Y，et al．Numerical methods for unsteady compressible multi-component reacting flows on fixed and moving grids［J］．Journal of Computational Physics，2005，202:710-736．

［7］ Kris R，Jan V，Erik D．An arbitrary Lagrangian-Eulerian finite-volume method for the simulation of rotary displacement flow［J］．Applied Numerical Mathematics，2002，32:419-433．