指数有界的广义算子半群逼近问题

陈 藏,王 剑

(华北科技学院教务处,北京 东燕郊 101601)

0 引言

自1942年,为了解决偏微分方程的初值问题,以E.Hille与K.Yosida为代表的一些数学家提出了Banach空间上强连续半群理论.此后,算子半群理论得到了不断的充实与发展.根据不同应用背景,C半群、积分半群等理论不断被提出[1-5],在解决偏微分方程领域起着非常重要的作用.分布参数控制系统,现代航天技术等工程领域中引人注目的问题的数学模型均为其有力的背景。

广义分布参数系统,即对时间的偏导数项的系数算子不一定可逆的系统,是由广义偏微分方程、广义积分方程或无限维空间中广义抽象微分方程所描述的系统的总称.由于其具有强有力的物理背景,如复合材料的温度分布问题、电磁耦合超导线路中的电压分布问题等,近年来得到了广泛的研究[6-10].文献[6]研究了下面的齐次与非齐次的广义分布系统

求解问题,其中E是有界线性算子,A为线性闭算子.通过研究发现上面的问题要想通过Laplace变换和卷积公式进行计算存在困难,由此提出了广义预解式和广义算子半群的概念,从而为研究上述广义系统的适定性提供了新的方法.该文,推导出指数有界的广义算子半群的Laplace逆变换的形式,并在预解式满足一定的条件时给出了指数有界的广义算子半群的留数型逼近公式.

1 定义及引理

定义1[6]设E是Banach空间上的有界线性算子,A是闭线性算子,称ρ(E,A)={λ:λ∈C,(λE-A)-1是Banach空间上的线性算子}为算子A的广义预解集,ρ(E,A)的余集称为A的E广义谱集,记为σ(E,A).对λ∈ρ(E,A),称R(λE,A)=(λE-A)-1为A的E广义预解式.

定义2[6]设X是Banach空间,B(X)是X上的有界线性算子全体,设单参数算子{T(t)}t≥0∈B(X),E是一个有界线性算子,若T(t+s)=T(t)ET(s),∀t,s≥0,则称{T(t)}t≥0是由E引导的广义算子半群,简称广义算子半群.

定义3[6]设A是X中的闭稠定线性算子,{T(t)}t≥0是强连续有界线性算子,且存在M>0,ω0∈R,使得‖T(t)‖≤Meω0t成立,E是一个有界线性算子,若下面的式子成立:

此时{T(t)}t≥0称为由E引导的以A为生成元的指数有界的广义算子半群.

引理1[6]若{T(t)}t≥0称为由E引导的以A为生成元的指数有界的广义算子半群,则下面的结论成立:

(i)T(t)T(s)=T(s)T(t),∀s,t≥0;

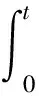
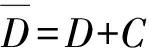
2 Laplace逆变换

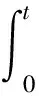
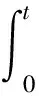
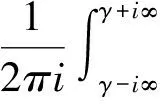
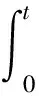
3 广义算子半群的留数型逼近

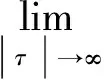
(1)

其中Ti(t)Ex=Resλ=λieλtR(λE,A)Ex,i=1,2，…,这里Reλm+1<β10.

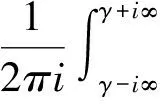
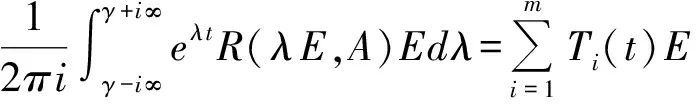
其中Ti(t)Ex=Reλ=λieλtR(λE,A)Ex,另一方面,

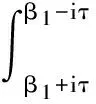
(2)

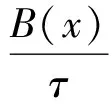
其中B(x)是与λ无关仅x与有关的常数,先令λ=μ+iτ,则

故当τ→∞时有

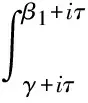
(3)

同理当τ→∞时有

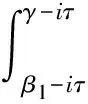
(4)

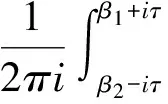
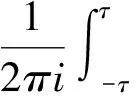
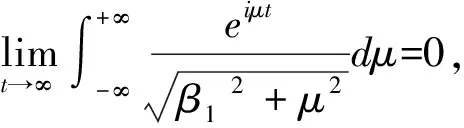
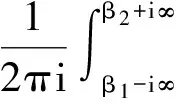
(5)

将(5)带入到(1)中即可完成证明.

[1] Tanaka N and Miyadera I.Exponentially Bounded C-Semigroups and Integrated Semigroups[J].Tokyo J.Math,1989，(1):99-115.

[2] NeubranderF.Integrated semigroups and application to the Abstract Cauchy problem.Pacific J of Math, 1988, 135(1):111-155.

[3] Zheng quan. Application of integrated semigroups to higer order abstract Cauchy Problem[J].Systems Science&Mathematical Sciences,1992,5(4):316-327.

[4] Ralph Delaubenfenls. C-Semigroups and strong continuous semigroups[J].Israel Journal of mathematics,1993,(1):227-255.

[5] 郑权,雷岩松.关于积分C半群[J].华中理工大学学报,2000,4(20):181-187.

[6] 葛照强,朱广田,冯德兴.广义算子半群与广义分布参数系统的适定性[J].中国科学:数学,2010, 40(5):477-495.

[7] Joder L, Femandez M L. An implicit difference methods for the numerical of solution of coupled system of partial differential equations [J]. Appl Math Comput, 1991,(46):127-134.

[8] Lewis F L.A review of 2-D implicit systems [J].Automatic, 1992,(28):345-354.

[9] Hu Y, Peng S G, Li X J. Maximum principle for optimal control problem of nonlinear generalized systems-infinite dimensional case[J].Acta Math Appl Sin,1992,(15):99-104.

[10] Trazska Z, Marszalek W. Singular distributed parameter systems [J]. IEEE Control Theory Appl, 1993,(40):305-308.

[11] Adrent W.Vector-Valued Laplace Transforms and Cauchy Problems [J]. Israel J of Math.1987,(59): 327-352.

[12] 钟玉泉.复变函数论[M].北京:高等教育出版社,1988.

[13] Hening B. A and Neubrander F. On Representations, Inversions, and Approximation of Laplace Transforms in Banach Spaces[J]. Appl. Anal.,1993,(49):151-170.