恒流静压导轨性能分析

2014-01-15刘明勇吴星辰

湖北工业大学学报 2014年2期

黄振，刘明勇，吴星辰

（湖北工业大学机械工程学院，湖北武汉430068）

静压导轨作为支承元件广泛运用于机械领域，向着能够在高速、超高速、高加速度、重载、多源强扰动的极端制造环境下制造极端尺度或极高功能产品的复杂系统方向延伸［1］。作为精密定位工作台的支承部件，是整个装备系统的关键部件，其性能的优劣直接影响到整个系统的精度和相应速度。国内外大多数学者运用数值法求解静压导轨的润滑特性时，忽略了静压导轨支承面因压力过大产生弹性形变的问题，对于一般的轻载、低速的静压导轨，由于油膜压力比较小，采用一般的数值计算的结果和实际的结果能够较好吻合。但是在高速重载工况下运动的导轨，尤其是低弹性模量材料的支承面使得在运动过程中产生的高压油膜压力对支承面产生较大变形，此时的理论计算结果就和实际结果有比较大的出入。

1 静压导轨的工作原理

1.1 恒流供油方式静压导轨工作原理

在高速重载工况下的静压导轨一般采用恒流量供油，润滑油从多头泵中送入导轨油腔，当导轨支承面上的油膜总压力和载荷相平衡时导轨浮起产生一定厚度的润滑油膜h0，多余的润滑油则通过封油边流回油箱（图1）［2］。

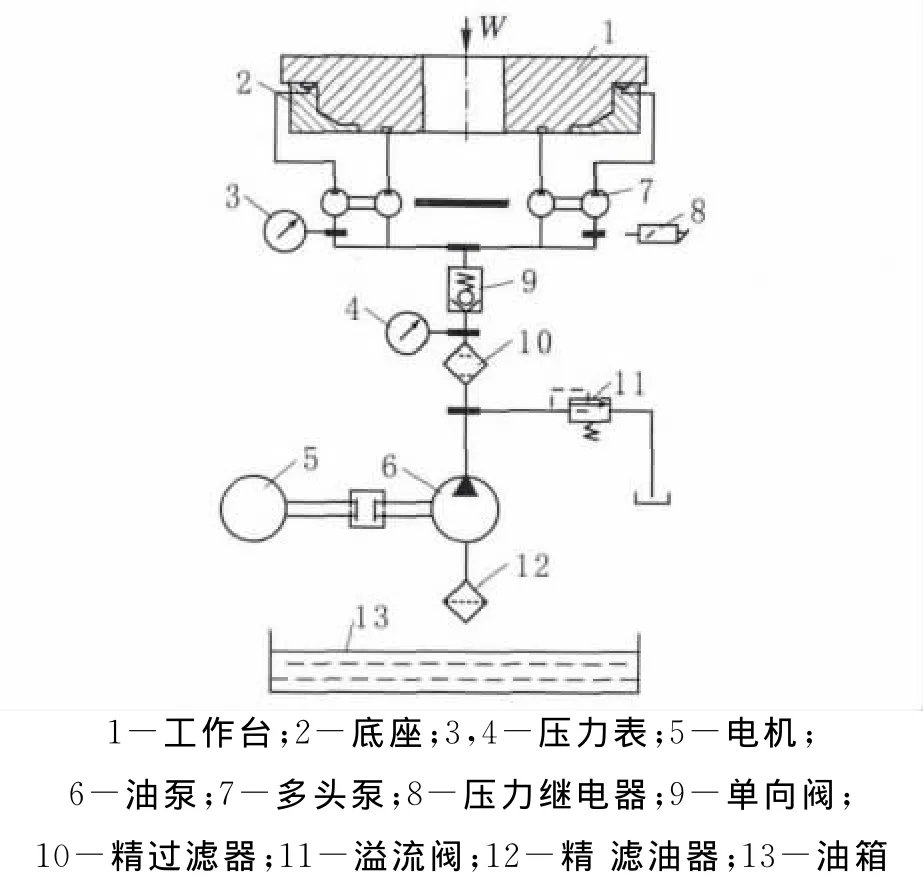
图1 恒流供油方式静压导轨

1.2 静压导轨润滑计算数值算法研究

对液体静压导轨的润滑计算主要是基于对经典润滑公式——Navier－Stokes方程的特殊形式雷诺方程的求解，雷诺方程是二阶偏微分方程［3］，以往依靠解析方法求解必须经过简化处理且只能得到近似解，因而会带来较大误差。随着计算机技术的迅速发展，先进的数值解法已经被引用到解决润滑问题中来，本文采用的是多重网格下的有限差分法求解雷诺方程。

根据实际工况对N－S方程推导出在高速重载下的油膜压力方程：

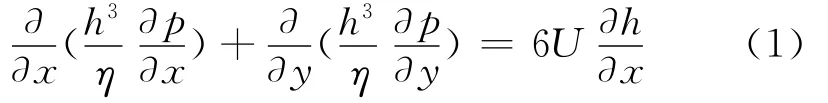
其中：p是油膜压力，h是油膜厚度，U是导轨的直线速度。将式（1）无量纲化后离散，得

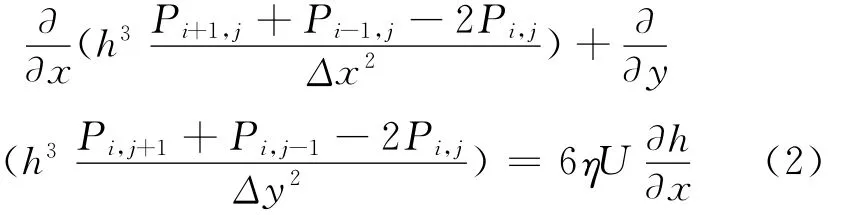
油膜厚度h是坐标x、y的函数，离散后的方程为：

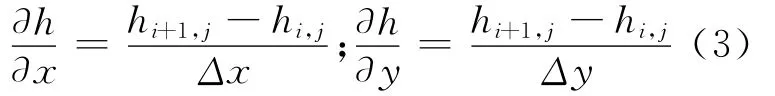
根据高速重载工况的特殊情况，将静压导轨支承面的弹性形变考虑到数值求解中，根据弹性力学可知［4］，在静压导轨支承面上的分布压力p（x，y）在表面上各点产生的变形位移

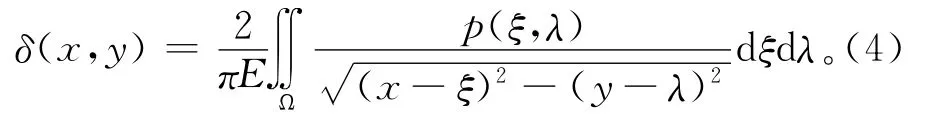
其中：E是导轨支承面材料的弹性模量，ξ和λ是对应x和y的附加坐标；Ω是求解域，在静压导轨中就是油腔区域。

2 静压导轨润滑问题计算

2.1 静压导轨物理模型

本文计算的静压导轨的几何模型是基于YK73125磨齿机上的工作台导轨，属于开式恒流供油类型，其简化的几何模型见图2。

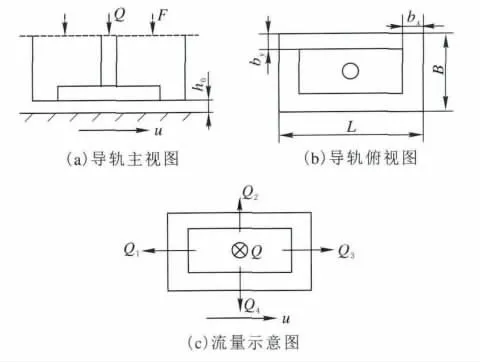
图2 静压导轨几何模型

在图2中，Q是流入导轨油腔的润滑油流量，2 000mm3／s；F 是工作载荷，1.344×103N；L、B分别是油腔x、y坐标方向的尺寸，60mm和120 mm；bx和by是封油边的宽度，均为15mm；Q1、Q2、Q3、Q4分别代表封油边1、2、3、4的流量。

2.2 油腔压力分布与油膜厚度的计算

在matlab中求解方程（1）中的p和h，可得相应的油膜压力分布和油膜厚度（图3）。

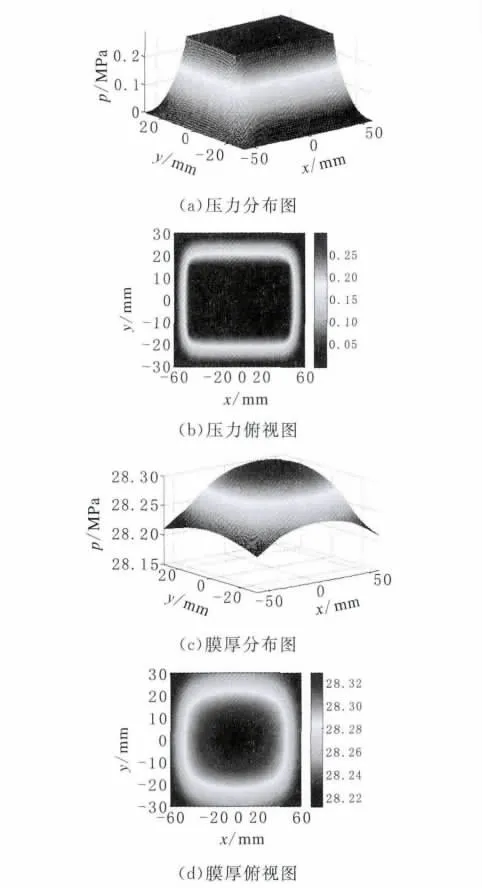
图3 静压导轨油腔压力分布和膜厚分布

由计算结果可以看出，压力分布图中中心位置的压力基本维持不变，但是从封油边出口位置的压力分布看，压力变化比较明显；从油膜厚度分布看，油腔进口处的油膜压力比较大，油膜厚度的形变显著。

油腔承载能力的大小是衡量静压导轨工作性能好坏的一个很重要指标［5］，承载能力与油腔的压力有着密切关系。将方程（2）中解出的Pi，j在求解区域Ω上积分求解，可得数值解下的油腔承载量

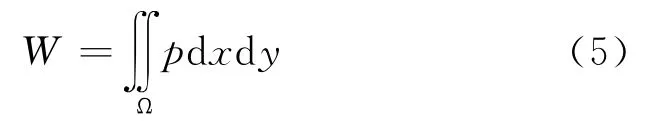
运用方程（2）中所解的压力分布，考虑到了静压导轨的弹性形变的压力，因而在数值计算上更加准确，更符合实际工况。

分析图3中特殊截面上的压力和膜厚数据，可以更加直观看出支承面弹性变形对油腔压力以及油膜厚度的影响（图4）。

分别截取坐标x、y方向的压力分布，图中虚线表示的是弹性形变下的油膜厚度，可以看出在计算工况下弹性变形对油腔压力几乎没有影响，膜厚差异小于0.1μm；对比封油边膜厚知，弹性变形使得边缘膜厚低于刚性假设计算的膜厚，且短封油边尤其明显。

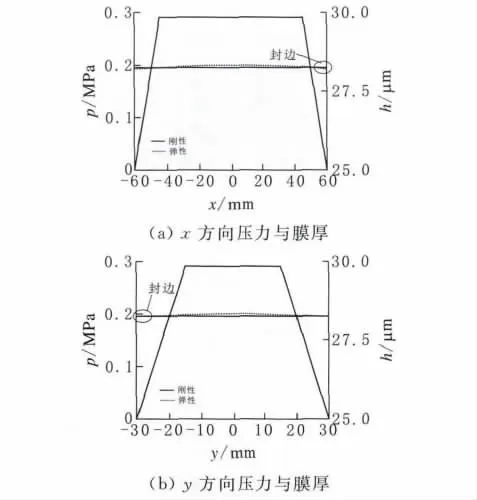
图4 弹性变形对油腔压力与膜厚影响

3 静压导轨润滑研究

3.1 流量对润滑的影响

在高速工况重载工况下的静压导轨供油流量对润滑性能有着较大影响，具体表现其在对油膜厚度、各封油边出口流量的影响［6］。将上述计算得出的压力分布数值解带入流量公式：

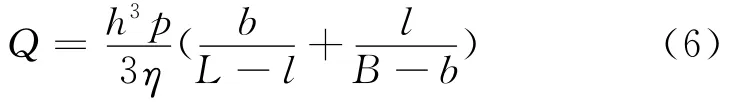
分别计算50～4 000mm3／s入口流量下的流量变化对膜厚影响。

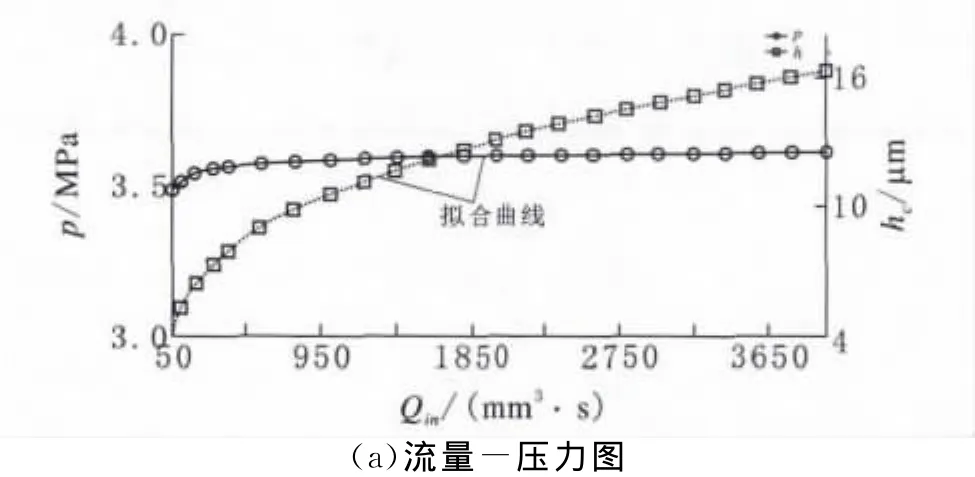
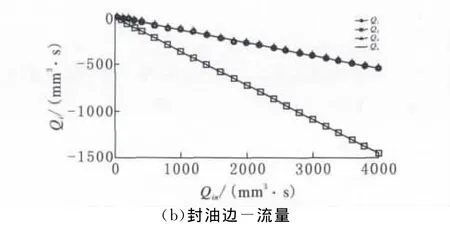
图5 流量对润滑的影响－压力图、封油边流量图

图5 a中，将压力曲线p和膜厚曲线在以流量为坐标的坐标系中表示，图5b中将4个封油边的流量大小以曲线的形式在总流量的坐标系中表示，可以根据所算数据得出压力和油膜厚度与流量的拟合方程：

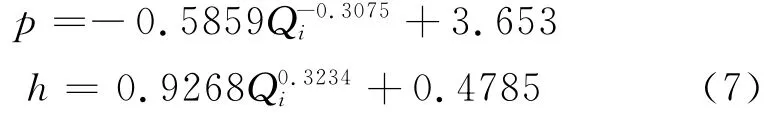
3.2 速度对润滑的影响

在高速重载条件下工作的静压导轨速度也是影响静压导轨运动状态的一个重要因素，在方程（1）中的速度U是指液体静压导轨两支承面的相对速度。本文计算选取了速度从1～5m／s的数据进行计算，分别求解速度与压力的关系、速度与流量的关系（图6）。

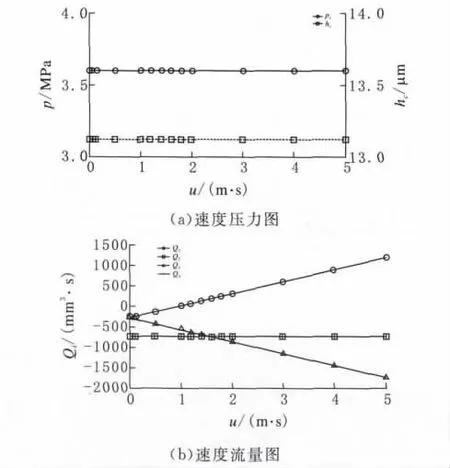
图6 速度－压力图、速度－流量图

由图6a知，静压导轨的运动速度对油腔润滑压力、膜厚没有影响，图6b表明，随着运动速度增大，封油边2和封油边4流量恒定，而封油边1和封油边3变化明显，其中封油边1流量值由负值向正值变化，说明该处由初始的出油转变为吸油，对应封油边3流出的流量增大。通常在导轨静压润滑中，封油边的吸油现象是不允许发生的，一般采用加大供油量的方式予以避免。