基于Matlab的高斯模糊图像去噪方法研究

周美丽，白宗文

（延安大学 陕西 延安 716000）

实际图像含有多种噪声，这些噪声可能在传输中产生，也可能量化处理时产生。噪声产生的原因决定了它的分布特性及它和信号的关系。根据噪声和信号的关系可将其分为两种形式：加性噪声，噪声图像可表示为噪声和信号的叠加，其特点是噪声和信号无关，如一般的电子线性放大器的噪声，不论输入信号大小，其输出总是与噪声相叠加；乘性噪声，噪声图像输出是两部分的叠加，第一项为信号本身，第二项为信号与噪声的乘积，其中第二项噪声受信号本身的影响，即噪声项受信号的调制。如光量子噪声、底片颗粒噪声都随信号增大而增大。乘性噪声模型和分析计算都比较复杂，当信号变化很小时，第二项近似不变，此时可用加性噪声模型来处理。通常总是假定信号和噪声是相互独立的，此类噪声与图像信号有关。

1 图像去噪方法

下面介绍几种图像去噪的方法：

均值滤波器[3]，这一滤波方法本质上就是线性平滑空间滤波器，是基于一种领域的操作，首先选用一定尺寸的模板，要处理的像素点位于模板的中心，随着模板的移动，完成对领域内所有像素的滤波。实际是对模板所包含的像素的简单平均，其平均值用来代替该像素原来的灰度，即是邻域平均技术。邻域平均法有力地抑制了噪声，同时也由于平均而引起了边界模糊现象，模糊程度与邻域半径成正比。为了尽可能地减少模糊失真，采用阈值法减少由于邻域平均而产生的模糊效应。其公式如下：

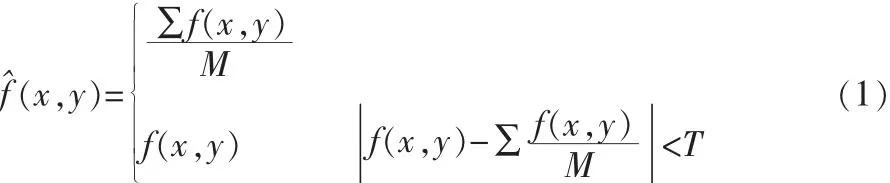
上述方法也可称为算术均值滤波器，此外还可采用几何均值滤波器、谐波均值滤波器和逆谐波均值滤波器。几何均值滤波器所达到的平滑度可以与算术均值滤波器相比，但在滤波过程中会丢失更多的图像细节；谐波均值滤波器对高斯噪声效果更好，但不适用于“胡椒”噪声；逆谐波均值滤波器更适合于处理脉冲噪声，但它必须要知道噪声是暗噪声还是亮噪声，以便选择合适的滤波器阶数符号。

自适应维纳滤波器[4]，它能根据图像的局部方差来调整滤波器输出，局部方差越大，滤波器的平滑作用越强。它的最终目标是使恢复图像（x，y）与原始图像 f（x，y）的均方误差最小，滤波效果比均值滤波器好，对保留图像边缘和其它高频分量很有用，但计算量较大。维纳滤波器对含有白噪声的图像滤波效果最佳。

小波去噪[5]，由小波变换的特性可知，高斯噪声的小波变换仍然是高斯分布的，它均匀分布在频率尺度空间的各部分，而信号则由于带限性，其小波变换系数仅仅集中在频率尺度空间上的有限部分，这样，从信号能量的观点来看，在小波域上，所有小波系数都对噪声有贡献，也就是噪声的能量分布在所有的小波系数上，而只有一小部分小波系数对信号能量有贡献，所以可以把小波系数分成两类：第一类小波系数仅仅由噪声变换后得到，幅值小，数目较多；第二类小波系数由信号变换得来，并包含噪声的变换结果，幅值大，数目较少。据此，可以通过这种小波系数幅值上的差异来降低噪声：对信号的小波系数设置一个阈值，大于该阈值者认为属于第二类系数，它同时含有信号和噪声的变换结果，可以简单保留或进行后续操作；而小于该阈值者则认为是第一类小波系数。即完全由噪声变换而来，应该去掉。这样就达到了降低噪声的目的。同时由于这种方法保留了大部分包含信号的小波系数，因此可以较好地保持图像细节。

2 去噪实验方法

在MATLAB平台下提供了好多详细滤波函数大大的简化了编辑程序工作量，使得整个仿真实验安全可靠[6]。针对高斯模糊图像这一类型，实验中采用均值滤波，维纳滤波和小波自适应阈值等6种方法分别去噪：1）对均值滤波：比较了一次、二次和三次均值滤波以去除更多的噪声；2）对于维纳去噪：采用了一次维纳去噪和一次维纳组合一次均值去噪；3）对于小波去噪，其消噪方式分为3类：①晟简单的强制消噪：它把全部高频系数置零，只用低频系数重构。在一个消噪处理中可重复应用：②最典型的默认阈值消噪：首先获取在消噪过程中的默认阈值；然后进行消噪；③独立阈值消噪：每层选取不同的阈值，这种阈值本文采用独立自适应阈值消噪以用于比较，对其子带阈值进行自适应确定，并给出了自适应阈值公式：

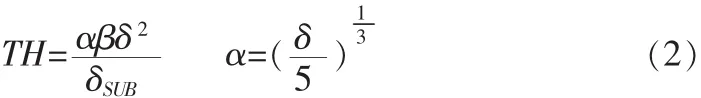
其中δ为图像噪声的标准差；β为尺度系数，相同分解层的子带，其参数相同；δsub是子带系数的标准差。δ可用如下公式进行估计：

HH1为一级小波分解的对角分量，β=LK/J，式中，J为分解的最大尺度；Lk为第k级子带的大小，对于M*N图像来说，LK=M*N/2k.这样针对每个子带可以利用上式确定出各自的阈值。采用自适应子带闽值比统一阈值能给出更好的降噪效果。

3 实验结果

取噪声方差δ2=1，用各种去噪方法所复原的图像如图1所示。由于直观视觉的局限性我们只能大体得出维纳去噪的视觉效果较好，二次均值其次，而小波变换去噪的效果对于高斯噪声而言并不是很好。

图1 高斯模糊图像去噪Fig.1 The Gauss-blurred image denoising

下面用图像的均方误差数据来比较各种去噪方法的优劣如表1所示。

表1 去噪图像均方误差Tab.1 The mean-square error of image denoising

通过对表1中图像均方误差数据的比较，我们可以得出，对于高斯噪声，无论噪声大小，维纳滤波的去噪效果总是最好的。

4 结 论

文中通过Matlab平台实验仿真比较了6种去除图像噪声的方法分别为一次、二次和三次均值滤波，一次维纳去噪，一次维纳组合一次均值去噪，以及基于独立自适应阈值的小波去噪。主观评判和客观计算数据的比较得出一个结论，即对于高斯噪声污染图像用维纳滤波法较其他方法去噪效果较好。

[1]刘跃.数字图像复原算法研究[D].贵阳：贵州大学，2006.

[2]鲁胜强.基于灰色系统理论的图像去噪算法研究[D].武汉：武汉理工大学，2007.

[3]胡浩，王明照，杨杰.自适应模糊加权均值滤波器[J].系统工程与电子技术，2002，24（2）：15-17.HU Hao，WANG Ming-zhao，YANG Jie.Adaptive fuzzy weighted mean filter[J].Systems Engineering and Electronics，2002，24（2）：15-17.

[4]顾亚芳.高斯模糊图像的盲复原[D].南京：东南大学，2005.

[5]刘涛.小波变换技术概述[J].信息技术，2010（22）：33.LIU Tao.The technique of wavelet transform[J].Information Technology，2010（22）：33.

[6]丁磊，潘贞存，丛伟.基于MATLAB信号处理工具箱的数字滤波器设计与仿真[J].继电器，2003，31（9）：49-51.DING Lei，PAN Zhen-cun，CONG Wei.The design and simulation of digital filter based on signal processing toolbox in MATLAB[J].Relay，2003，31（9）：49-51.