一种基于延迟插入法和云计算系统的快速电路仿真的研究

周小娟

（西安外事学院 计算机中心，陕西 西安 710077）

随着集成电路技术的发展，高速和高密度电路已经越来越多的被应用于芯片和电路板设计中，然而，在信号和电源的集成过程中一些严重的问题不断出现，降低了电路的设计效率。人们迫切希望一些先进的仿真技术出现，应用这些仿真技术，可以验证高速信号对电路整体产生的各种影响，从而提高设计效率。

本文通过对大规模电路设计中常用的一种快速瞬变仿真方法--延迟插入法进行研究，发现延迟插入法的算法并不需要复杂的矩阵操作，这种算法可以进行并行运算，这正是云计算的显著特征。通过在一个云计算系统中运行并行分布式延迟插入法的算法，并对一个常用的电源分配电路模型进行分析，本文得到了新颖的仿真计算结果，从而为快速电路的仿真技术提供了一种新的思路。

1 延迟插入法

延迟插入法是一种以快速瞬变分析中的跳跃算法为基础的电路仿真方法。不同于传统的以集成电路为重点的仿真程序需要花费很多时间使用LU分解方法来分解大规模的系数矩阵，延迟插入法的算法不需要直接进行矩阵运算。并且，延迟插入算法具有计算效率随着计算量线性增长的特征，和传统的仿真算法相比，在大规模电路中延迟插入法具有仿真速度更快的优势。

延迟插入法的算法要求被分析的电路由分支拓扑结构和节点拓扑结构组成。如图1所示，分支拓扑结构由串联连接的电阻 Ra，b，电感 La，b，和独立的电压电源 Ea，b 组成，它们被放置在节点Va和Vb之间。如图2所示，节点拓扑结构由并行连接的电导Ga，电容Ca和独立的电流电源Ha组成，它们各自独立的连接在节点Va和参考节点之间。本图中参考节点为接地节点。

图1 适用于延迟插入法的分支拓扑结构Fig.1 Branch topology for latency insertion method

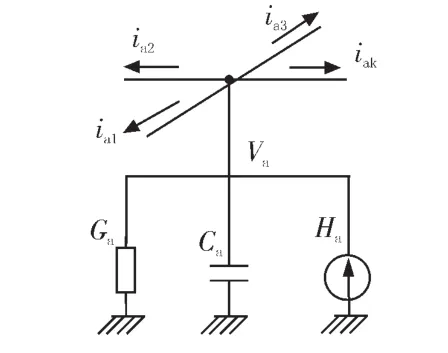
图2 适用于延迟插入法的节点拓扑结构Fig.2 Node topology for latency insertion method

概况起来，适用于延迟插入法的电路网络拓扑需要满足：每个分支都必须包含一个电感，每个节点必须包含一个接地电容。这个电感和电容就是用来在各自的拓扑中产生延迟。使用有限差分法对分支拓扑应用本基尔霍夫电压定律（KVL）和对节点拓扑应用基尔霍夫电流定律（KCL）[2]，我们可以得到延迟插入算法的如下公式，

上式（1）和（2）中，n 为步长，Δt为步长大小，是连接到节点a的分支个数，分支电流的步长和节点电压的步长相差半步。通过变换（1），（2）式子，我们可以得到分支电流和节点电压的表达式，

上式（3）和（4）表明分支电流和节点电压第（n+1）个和第（n+1/2）个步长的数值只依赖于它们前一个步长的值。因此从计算开始，随着时间的持续，可以累积递归计算出分支电流和节点电压在每一个步长的值。

通过公式（3）和（4），我们还可以看出延迟插入法中分支电流和节点电压可以被独立的表示，并且可以由独立的两个不同的计算过程进行计算。也就是说，如果要计算任意给定步长的分支电流，单个分支的电流并不需要参考同一步长时其它分支的电流，它只需要参考它自己过去步长的电流就可以了。这个规律同样适用于节点电压的计算。因此，对各个不同分支电流的计算和各个不同节点电压的计算是解耦的，它们可以被并行计算，这就是所谓的并行分布式延迟插入法。

2 研究方法和数据

为了验证并行分布式延迟插入法的有效性，我们设想准备了如图3所示的一个平面等效电路，它一共有400个单元。我们使用波形延迟为0.2 ns，上升时间为0.1 ns，脉冲宽度为1.0 ns，和振幅为0.05 A的电流作为输入电流。我们选择了著名的通用电路模拟程序软件HSPICE的仿真结果作为参考，来比较并行分布式延迟插入法的仿真结果的有效性。

图4是HSPICE软件和并行分布式延迟插入法的瞬态仿真结果对比图，我们可以看到这两种仿真方法的结果基本一致，并行分布式延迟插入算法和HSPICE之间有良好的一致性。这证明了并行分布式延迟插入法的仿真结果是有效的。

图3 验证并行分布式延迟插入法的平面等效电路Fig.3 Equivalent plane circuit for validity parallel-distributed latency insertion algorithm

图4 HSPICE软件和并行分布式延迟插入法（LIM）的瞬态仿真结果对比图Fig.4 Transient simulation result comparison of HSPICE and paralleldistributed latency insertion method

为了验证并行分布式延迟插入法的性能，仿真测试单元数为1 000 000，400 000和9 000 000的平面电路，来仿真其瞬态响应。如此大量的测试单元，如果使用正常的仿真手段，其计算量将是巨大而漫长的。延迟插入法的并行分布式特性，使我们想到了借助云计算系统的集群运算来加速我们的仿真计算。

通过使用亚马逊的云服务平台系统Amazon EC2，这里我们获得了一个可以最多提供32个四核CPU，即128核的云系统。图5显示了在不同数量的CPU核运行的情况下，计算时间的变化。我们可以看到在核数目增加到32个CPU核之前，计算时间随着核的数目增加而单调递减，在32个CPU核数目之后计算时间没有大的变化。图6显示了运算加速率和CPU核数目之间的关系。我们可以看到在CPU核数目增加到32个之前，计算加速率在线性增长，在32个CPU核之后，加速率没有大幅变化并且变化显得没有规律。

图5和图6的分析结果告诉我们，32个CPU核的计算时间比单个核的计算时间快25倍左右。尽管在CPU核的数目增加超过32个后，计算时间变化无规律，但总体上都是围绕在32个CPU核的计算时间的周围。我们可以认为，计算速度的加速率在CPU核的数目增加到32个之后，CPU和内存之间数据传输遇到了瓶颈，并不能单纯的依靠增加CPU核的数目来提高计算性能。作为一个结果，我们可以认为在理想情况下，即CPU的数目和内存的配置达到了最优，云计算系统的计算性能随着CPU的数量增加而单调增加。图5和图6的仿真数据同时说明在仿真大规模电路时并行分布式延迟插入法的性能是高效的。

图5 运算时间和CPU核数目对比图Fig.5 Execution time vs number of cores

图6 运算加速率和CPU核数目对比图Fig.6 Speed up ratio vs number of cores

3 结 论

本文通过对延迟插入法进行研究，推导出了大规模电路中分支电流和节点电压的仿真计算公式，并且发现了对不同的分支电流和节点电压其可以并行计算的特征。通过和通用电路模拟程序软件HSPICE的仿真结果进行比较，验证了延迟插入法仿真结果是有效的。通过在云计算系统上应用延迟插入法对超大规模平面电路进行仿真计算，验证了延迟插入法的计算性能是高效的。通过延迟插入法和云计算系统的结合来仿真大规模快速电路是有效，高效和可行的。

[1]张松兰.仿真软件在电路仿真中的应用[J].蚌埠学院学报，2013（3）:1-2.ZHANG Song-lan.Application of simulation software in electric circuit[J].Journal of Bengbu College，2013（3）:1-2.

[2]张雷雷，沈海斌.新型振荡采样随机源电路与快速仿真[J].半导体技术，2011，36（4）:307-308 ZHANG Lei-lei，SHEN Hai-bin.New oscillator-based random source circuit and fast simulation[J].Semiconductor Technology，2011，36（4）:307-308.

[3]李勇峰，黄娟，王龙业，等.基于HSPICE的基准电压源的分析与仿真[J].西藏科技，2012（4）:75-76.LI Yong-feng，HUANG Juan，WANG Long-ye，et al.Analysis and simulation based on HSPICE voltage reference[J].Tibet’s Science and Technology，2012（4）:75-76.

[4]张新玲，张东，曹玲玲，等.云计算虚拟化平台性能研究[J].软件导刊，2013（11）:1-2.ZHANG Xin-ling，ZHANG Dong，CAO Ling-ling，et al.Research of cloud computing virtualization platform performance[J].Software Guide，2013（11）:1-2.

[5]林军青，林锦贤.面向云计算的服务性能模型研究[J].电子设计工程，2011（19）:22-23.LIN Jun-qing，LIN Jin-xian.Research on a service performance model orienting cloud computing[J].Electronic Design Engineering，2011（19）:22-23.

[6]王秀梅.LabVIEW在模拟电子电路设计与仿真中的应用[J].电脑知识与技术，2013，9（18）:4328-4329.WANG Xiu-mei.LabVIEW applications in analog electronic circuit design and simulation[J].Computer Knowledge and Technology，2013，9（18）:4328-4329.

[7]杨文志.云计算技术指导南[M].北京:北京工业出版社，2010.