石灰处理软土路基当量回弹模量换算新方法

2014-01-13袁文瑞李笑笑

交通运输研究 2014年21期

袁文瑞，李笑笑

（1.河北工业大学土木工程学院，天津300401；2.天津市海顺交通工程设计有限公司，天津300400）

0 引言

天津市地处九河下梢，地下水位较高，土质多为软土，土中多含大量腐殖质，土基承载力极低，土基回弹模量往往难以达到规定的要求，对路面结构的承载能力和整体稳定性造成不良影响。因此通常情况下需要对软土路基进行加固处理。石灰加固软土具有就地取材、造价低廉、容易施工等优点，并且具有较高的强度、较强的板体性等，利用石灰处理软土路基以提高土基回弹模量是工程中经常采用的技术措施，取得了不错的效果。

原则上说，石灰处理软土层既可以作为路基的组成部分，也可以作为路面结构层。考虑到增设石灰土层是为了保证路基的回弹模量值，从设计的角度，应将石灰土层作为路基的组成部分。石灰土层和原状软土层对路面结构的支撑作用可以仅用一个模量参数（路基顶当量回弹模量）表征。为了得到一个代表路基对面层支承作用的模量参数，往往是利用弹性层状理论，将多层体系换算成当量的均质体系。现行刚性路面设计规范中给出了路基模量转换诺谟图，即按双层体系理论解绘制的双层体系顶面当量弹性模量换算曲线（施压面的半径为15cm，层间为连续接触）。利用此曲线图，可按上层的厚度h和模量Ex及下层的模量E0确定路基顶面的当量模量Et。通过分析计算石灰土在不同处理情况下路基顶面的当量回弹模量，可以为道路的路基设计方案提供理论依据。然而，在规范应用过程中发现，双层弹性体系理论解的回归公式仅适用于石灰土回弹模量与软土回弹模量比值较大的情况，否则换算误差较大。为此，本文以弯沉等效的原则对双层弹性理论解的回归公式作进一步分析，并通过大量计算分析，回归出了适合天津地区石灰处理软土路基的精度更高的顶面当量回弹模量计算公式。

1 现行设计规范换算方法的缺陷

现行的当量回弹模量换算方法，是按双层弹性体系理论解的回归公式确定均质体的当量回弹模量，即：

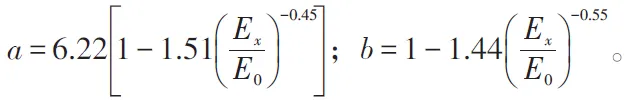
对式（1）深入分析后发现，该式对于Ex/E0≥8时应用精度较高，但是如果Ex/E0＜8时，随着模量比降低，误差越来越大，甚至会出现当量回弹模量小于土基模量的反常现象。为了进一步说明这一点，可以进行几个简单的算例分析。表1是对于同样的路面结构，以Kenpave 程序计算结果为基准，将规范中的换算结果与之对比。

表1 不同路面结构当量回弹模量换算结果比较

由表1可以看出，规范中当量回弹模量换算公式在Ex/E0＜8时已不再适用，否则将使设计结果显得过于保守和不合理。随着公路等级的提高和高模量材料的大量使用，Ex/E0值也随之有所增大，但是在目前干线公路上Ex/E0＜8 的情况也是常有的，尤其是在天津地区，存在大量软土路基，上层软土虽经过石灰处理，但模量仍比较低，资料显示大概在30～100MPa 之间。为了得到适合天津地区石灰处理软土路基当量回弹模量的换算公式，有必要对双层弹性体系理论解重新进行回归分析。

2 拟合当量回弹模量计算公式

多层结构路基顶面和弹性半空间体圆形均布荷载中心处的竖向位移（弯沉）可分别表示为式（2）和式（3）。

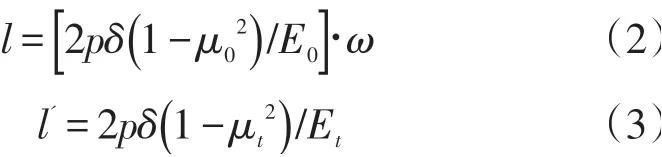
式中：p为均布荷载压强（MPa）；δ为荷载作用半径（cm）；μ0、μt分别为软土和弹性半空间体的泊松比；E0、Et分别为软土和弹性半空间体的回弹模量（MPa）；ω为位移系数。

根据弯沉等效原则，多层弹性结构可以等效为弹性半空间体，即弹性半空间体的回弹模量Et满足l=l′，此时回弹模量Et称为路基顶当量回弹模量。

本文采用Kenpave程序计算弯沉。计算时，石灰土表面作用半径为15cm、压强为700kPa 的圆形均布荷载，双层体系结构计算参数如图1所示。

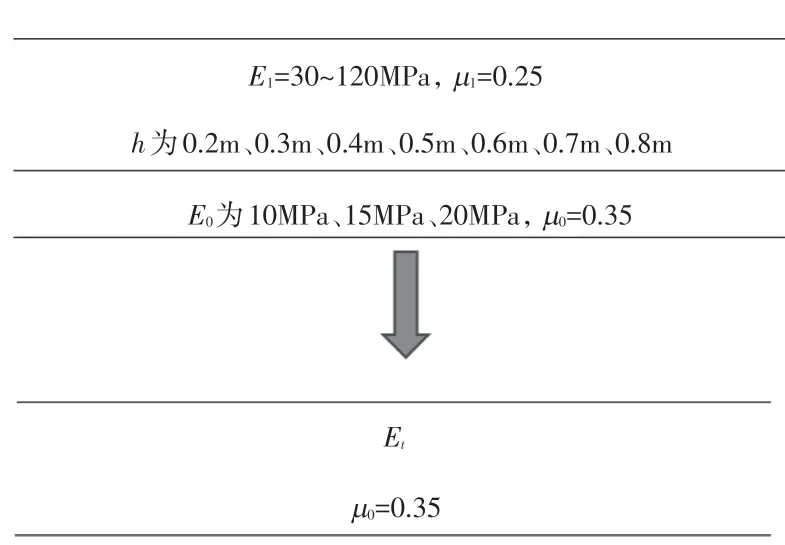
图1 转换模型及双层体系结构计算示意图

假设顶面的当量回弹模量值是下层土基的回弹模量值E0以及上层石灰稳定土模量Ex与厚度hx及泊松比的函数。泊松比对计算结果的影响非常小，可以忽略不计。因而，在土基回弹模量E0和路基顶当量回弹模量Et之间可以建立起如下函数关系，见式（4）。

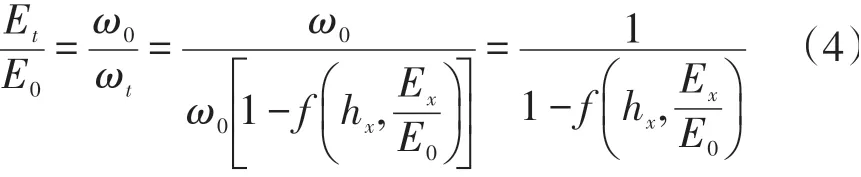
式中：Et为路基顶当量回弹模量（MPa）；E0为土基回弹模量（MPa）；Ex为石灰稳定土回弹模量（MPa）；h为石灰稳定土厚度（m）；ω0为E0所对应的弯沉值；ωt为Et所对应的弯沉值。

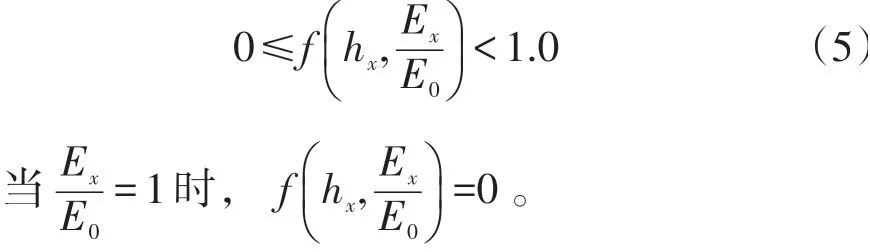
应用Minitab 统计分析软件对各种结构组合下的一系列数据进行回归分析，从而得到相应的因变量与自变量之间的换算回归公式。参考规范中计算公式的形式，设：

根据弹性层状体系地基的计算结果进行回归分析可以得到：

式中：Et为路基顶当量回弹模量（MPa）；E0为土基回弹模量（MPa）；Ex为石灰稳定土回弹模量（MPa）；h为石灰稳定土厚度（m）。

该回归公式的R2=0.976，说明该公式回归相关性非常好。

3 当量回弹模量公式的误差比较

为了验证式（7）的精度与可靠性，表2 列出了双层结构的大量计算结果，并分别与弹性层状体系理论解和规范解做了比较。弹性层状体系理论解采用KENPAVE程序直接按双层结构计算弯沉值ωt，然后按计算得出当量回弹模量。表2列出了回归公式（式（7））和规范中当量回弹模量计算公式（式（1））与弹性层状体系理论解的比较。

表2（续）

从表2 中可以看出，规范公式在模量比大于8时的误差比较小，模量小于8时的误差非常大，甚至可以达到69%。在天津这种软土分布广泛的地区，石灰土与软土模量比小于8是难免的，因此规范中的公式已不再适用。本文拟合公式（式（7））相比于规范公式（式（1）），其计算结果更接近于弹性层状理论解的结果，误差相对规范公式减小很多，基本上都在10%以内。这说明按等效弯沉原则将双层结构转化为当量单层结构后，确定软土路基均质体的当量回弹模量是可行的。