基于矢量控制的步进电动机细分驱动技术

苏义鑫，孙功武，聂 巍

(武汉理工大学，湖北武汉430070)

0 引 言

步进电动机具有误差不积累、结构简单、体积小、价格低廉、控制方便等优点，因而被广泛应用在数控、印刷、喷绘、光学定位、机器人等行业［1－3］。但步进电动机因为固有步距角大、低频运行有振动、高频失步等问题，不能直接应用在控制精度要求较高的场合。采用步进电动机细分驱动技术可以较好地减小步进电动机的步距角，抑制步进电动机的振荡，改善步进电动机的运行性能［4］。文献［5］采用恒流斩波细分驱动控制技术和等步距角的细分控制策略实现了128 细分;文献［6］将量化后的正余弦电流作为步进电动机的细分电流，并将该细分电流制成表格，然后利用查表法得到期望的绕组电流，最后根据采样的实际电流值进行相应控制，最多可实现256 细分驱动。这两种方法都可以提高步进电动机的控制精度，增加电机运行的平稳性，但不能做到真正的任意细分，具有一定的局限性。由于三相混合式步进电动机的工作原理与同步电机相似，因此本文借鉴同步电机的矢量控制技术，利用矢量控制思想和SVPWM 技术设计三相混合式步进电动机细分驱动系统。常规SVPWM 算法将电压矢量圆划分为6 个扇区，并且逆变桥各相导通时间的计算过程涉及多个中间变量［7－9］，计算比较繁琐，因此设计SVPWM 简化算法来缩短程序执行时间对提高系统的实时性有着重要意义。

1 系统设计

1.1 步进电动机数学模型

步进电动机是一个多变量、非线性、强耦合的系统，并且电机的转子相对于定子是相对运动的。为简化分析，做如下假设［10－12］:①电机三相绕组完全对称;②忽略磁路饱和和磁滞损耗;③气隙磁通在空间按正弦分布;④电机的参数恒定。步进电动机在d－q 坐标系中的数学模型如下:

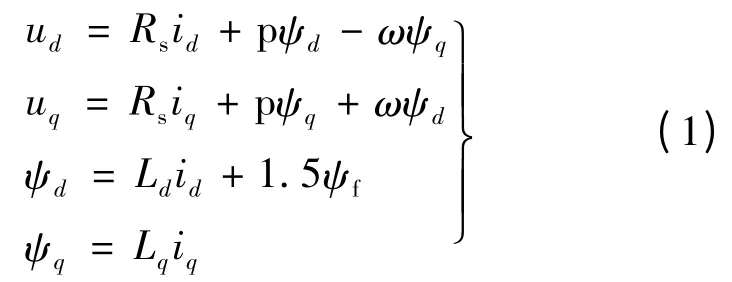
式中:Rs为定子电阻;id和ud分别是定子电流和定子电压在d 轴上的分量;iq和uq分别是定子电流和定子电压在q 轴上的分量;Ld和ψd分别是电感和磁链在d 轴上的分量;Lq和ψq分别为电感和磁链在q 轴上的分量;p 是微分算子。在d－q 坐标系中三相混合式步进电动机的电磁转矩:

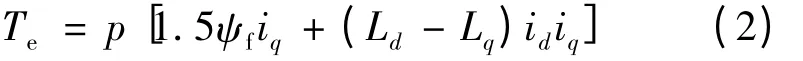
式中:p 为电机的极对数;ψf为磁体磁链，是定值;若id=0，则id和iq的合成矢量就为iq，电磁转矩方程变成:

由式(3)可知，此时电机的电磁转矩Te和iq呈正比，因此只要控制id=0、iq为恒值，就能精确地控制合成电流矢量，进而实现对转子位置的精确控制，且此时电磁转矩Te保持不变，实现恒转矩控制。

1.2 矢量控制的实现

系统矢量控制框图如图1 所示。采用id=0 的控制策略，为了减小步进电动机驱动器的体积，降低驱动器价格，省去了速度环和位置环，只保留了电流环。

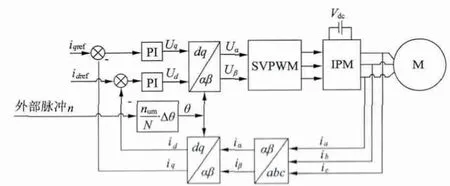
图1 系统矢量控制框图

图1 中，idref=0;iqref为设定的恒定值;N 为设定的细分数，可以为任意正整数;n 为外部脉冲的计数值;Δθ 为步进电动机的固有步距角，由电机参数决定;Vdc为直流母线电压。首先，经过Clarke 变换和Park 变换，将采样到的三相定子电流变换到d－q 坐标系下，求出id和iq;然后分别将idref、iqref和id、iq作差，差值经过PI 控制器调节后得到ud和Uq;将得到的ud和Uq经Park 逆变换到α－β 坐标系下，求出Uα和Uβ;最后通过SVPWM 算法计算输出。其中，θ=Δθ·n/N，N 越大，外部每来一个脉冲，θ 的增量就越小，因此只要N 设置足够大，θ 角的划分就足够细，就可以有效地抑制步进电动机的振动。由于本系统的细分数N 可以设置为任意正整数，所以可以实现任意正整数细分驱动。

2 SVPWM 简化算法设计

2.1 常规SVPWM 算法

常规SVPWM 算法中，三相逆变桥上桥臂的八种工作状态对应八种电压矢量:U0(000)、U1(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、U7(111)，其中U1(001)～U6(110)为有效的电压矢量，U0(000)和U7(000)为零矢量。六个有效电压矢量将电压矢量圆划分为六个扇区，如图2 所示［13］。

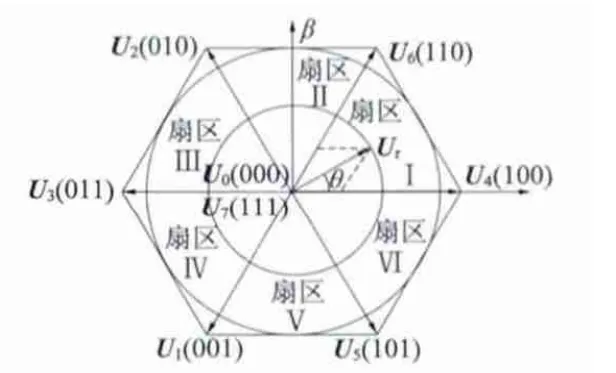
图2 基本电压矢量和扇区示意图

图2 中，Ur为合成电压矢量，且Ur为构成Ur所在扇区的两个有效电压矢量和零矢量合成。Ur所在的扇区可根据两相静止坐标系上的电压矢量Uαr和Uβr在三相静止坐标系上的投影U1、U2和U3确定。定义:若U1＞0 ，则A=1，否则A=0;若U2＞0，则B=1，否则B=0;若U3＞0 ，则C =1，否则C =0。令N =4C +2B +A，根据N 的值即可判断出Ur所在的扇区Sector。定义三个变量X、Y 和Z，令:

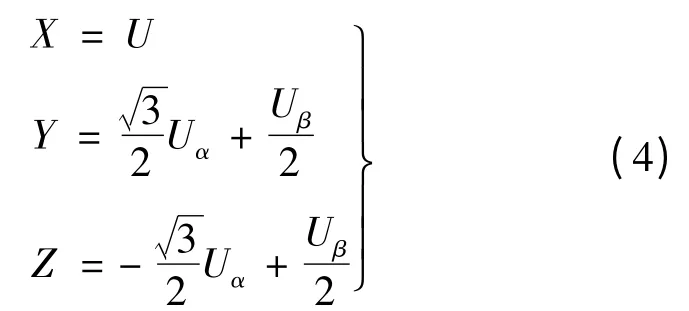
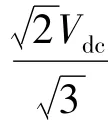
表1 相邻电压矢量作用时间

查表1 得出相邻电压矢量作用的时间t1、t2后，再计算出每一相对应的占空比ta、tb和tc。A、B、C三相桥的实际导通时间占空比Ta、Tb和Tc可根据所在的扇区来确定，具体如表2 所示［14］。

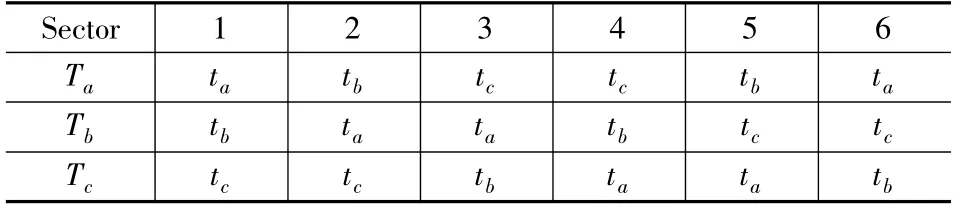
表2 三相桥每相导通时间占空比

通过上述计算和分析，可求出三相桥各相导通时间的占空比，根据导通时间占空比即可确定DSP中的比较寄存器的值，在软件中将比较寄存器的值修改为期望值即完成了SVPWM 算法。

2.2 SVPWM 简化算法

通过分析发现，常规SVPWM 算法涉及多个中间变量的替代，需要多次根据合成矢量所在扇区进行时间分配，可对常规的SVPWM 算法做适当简化处理。当合成电压矢量位于图2 中的扇区1 时，三相桥各相的导通时间占空比根据常规SVPWM 算法有:

当合成电压矢量位于与扇区1 对角的扇区4时，三相桥各相的导通时间占空比根据常规SV－PWM 算法有:

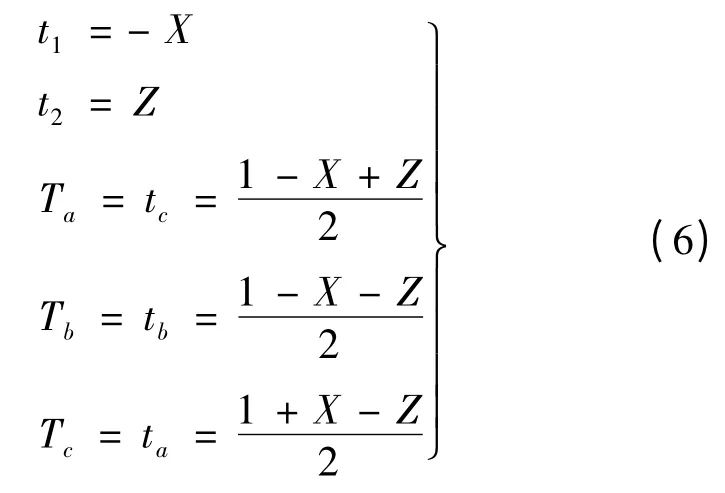
通过比较式(5)和式(6)发现，当合成矢量分别位于扇区1 和扇区4 时，虽然在两扇区中t1和t2的表达式各不相同，表2 中的分配情况也不同，但在两扇区内三相桥最终实际作用时间占空比的表达式用X、Y 和Z 表示是相同的。同理可以分析出合成矢量分别位于扇区2 和扇区5、扇区3 和扇区6 时有相同的结果。因此可利用这个特点对常规SVPWM 算法进行简化，将图2 中互为对角的两个扇区合并为一个区域，重新划分成如图3 所示的3 个区域。

SVPWM 简化算法将矢量圆划分为3 大区域，根据几何知识，合成矢量位于的区域可根据点(Uα，Uβ)和点(0，0)两点连线所成直线的斜率k 确定。三相桥每相导通时间占空比可以在常规SVPWM 算法的基础上推导总结出来，具体区域判断和每相桥导通时间占空比如表3 所示。

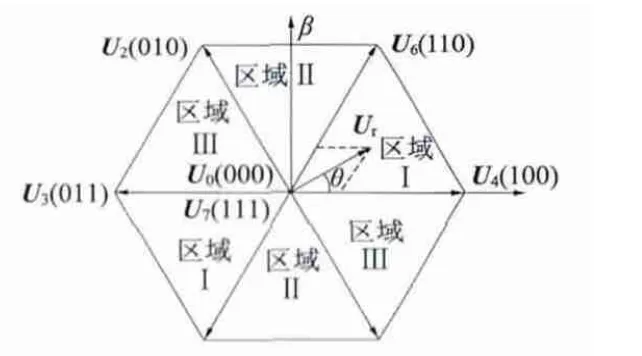
图3 三区域划分示意图

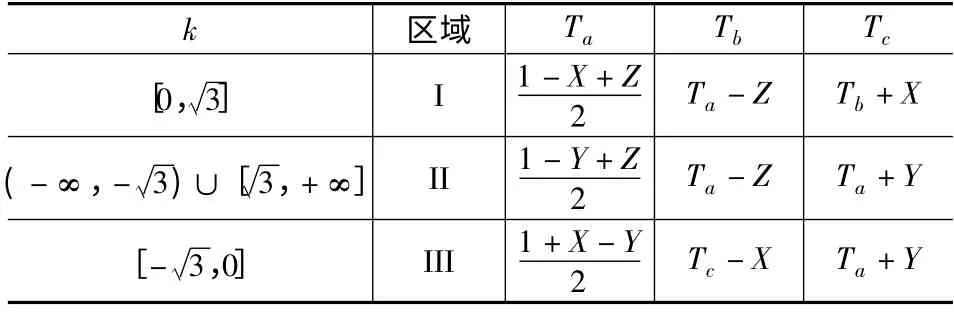
表3 区域判断及每相桥导通时间占空比

SVPWM 简化算法首先根据Uα和Uβ确定合成矢量位于的区域，然后查表3 就可以直接得出每相桥的导通时间占空比。和常规SVPWM 算法相比，简化SVPWM 算法减少了中间变量和扇区判断次数，计算过程更加简洁方便。

3 仿真与实验结果

在MATLAB 中对步进电动机细分驱动系统进行仿真，设置系统参数:Ld= Lq=0.045 H，Rs=1.5 Ω，id=0，iq=3.5 A，电机齿数为50，直流母线电压Udc=30 V，设置外部脉冲频率为300 Hz，细分数为10，即电机转一圈为3 000 步，每步0.12°。理论上未细分前，外部每发出6 个脉冲，合成电流矢量旋转一圈，10 细分后，外部每发出60 个脉冲，合成电流矢量绕圆形磁场旋转一圈。仿真结果如图4 所示。

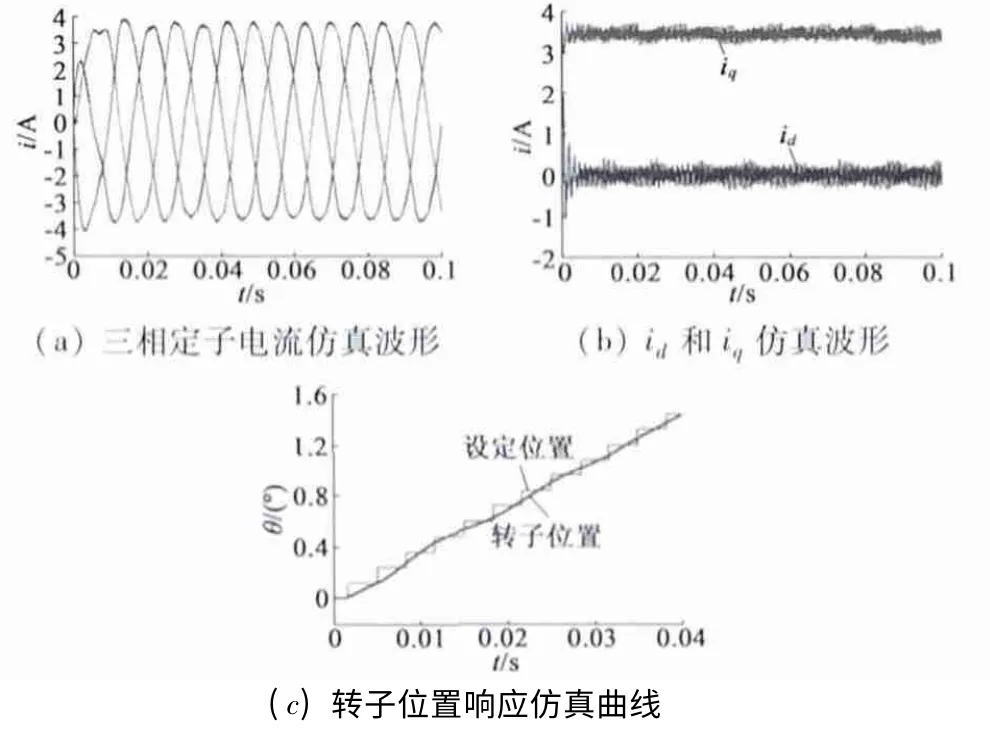
图4 仿真结果

图4(a)是定子三相电流波形，各相电流近似为周期0.2 s 的正弦电流，且相位相差120°。说明合成电流矢量绕圆形磁场旋转一圈需要0.2 s，转换成外部发出的脉冲数为60 个，与理论分析相一致，说明系统实现了10 细分驱动。图4(b)中，iq和id基本稳定在设定的3.5 A 和0，说明电机电磁转矩基本稳定。图4(c)为步进电动机转子位置响应曲线，电机转子是连续变化的，改善了步进电动机运行出现的“步进”现象，有利于抑制电机抖动。

实验平台采用雷赛573S15 三相混合式步进电动机，电机转子齿数为50，额定电流5.8 A;开关电源提供24 V 直流电压;设置细分驱动器的id=0，iq=2 A，细分后每圈3 200 步，外部脉冲频率为1 kHz，则理论上得到三相电流是周期为64 ms 正弦电流。实际得到采样并转换后的A 相和B 相电流波形如图5 所示。

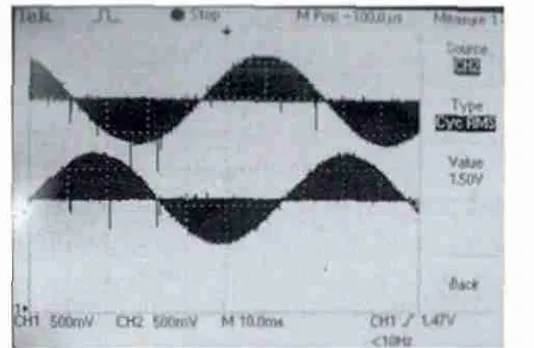
图5 采样并转换后的电流波形

图5 转换后的电流波形为周期64 ms、相位互差120°的正弦波，与理论分析相一致，此时电机运行比较平稳，没有抖动和噪声。我们分别采用常规SVPWM 算法和简化的SVPWM 算法设计程序，并比较程序执行一次所需时间，结果如表4 所示。

表4 程序执行时间对比

从表4 中可以看出，相对于采用常规SVPWM算法设计的程序，采用简化SVPWM 算法设计程序执行速度要快12%。

4 结 结

本文首先建立了三相混合式步进电动机数学模型，然后利用矢量控制思想设计步进电动机细分驱动系统，最终实现了步进电动机恒转矩、等步距角任意细分驱动。采用该细分驱动技术，提高了步进电动机控制精度，增加了步进电动机运行平稳性，使步进电动机能够应用在控制精度要求更高的场合。同时，本文在常规SVPWM 算法基础上，设计了一种SVPWM 简化算法。SVPWM 简化算法的计算过程比常规SVPWM 算法计算过程更加简洁清晰，利用该简化算法设计的程序，执行速度更快，效率更高，从而可以适当降低系统对DSP 处理速度的要求，具有一定的工程应用价值。

［1］ de Lucena S E，Kaiser W.Stepping－motor－driven constant－shear－rate rotating viscometer［J］. IEEE Transactions on Instrumentation and Measurement，2008，57(7):1338－1343.

［2］ Melin P，Castillo O.Intelligent control of a stepping motor drive using an adaptive neuro－fuzzy inference system［J］.Information Sciences，2005，170(2－4):133－151.

［3］ 赵大威，姜力，金明河，等.仿人型机器人手的力矩保持功能及控制系统［J］.电机与控制学报，2007，5(11):497－501.

［4］ Yang Shengming，Lin Fengchieh，Chen Mingtsung.Micro－stepping control of a two－phase linear stepping motor with three－phase VSI inverter for high－speed applications［J］.IEEE Transactions on Industry Applications，2004，40(5):1257－1264.

［5］ 惠晶，肖荣.一种实用的步进电机细分驱动控制系统［J］.微电机，2009(10):87－89.

［6］ 杨韬仪，王辉，徐锋.两相步进电动机细分方法研究［J］. 微电机，2007(9):69－71.

［7］ 周卫平，吴正国，唐劲松，等.SVPWM 的等效算法及SVPWM 与SPWM 的本质联系［J］. 中国电机工程学报，2006，26(2):133－ 137.

［8］ Tang Jian，Guo Yuhua，Lian Jisan. An efficient SVPWM algorithm with low computational overhead for three－phase inverters［J］.IEEE Transactions on Power Electronics，2007，22(5):1797－1805.

［9］ Yan Shijie，Zhang Qun，Du Heng. A simplified SVPWM control strategy for PV inverter［C］//Proceedings of the 24th Chinese Control and Decision Conference.IEEE，2012:225－229.

［10］ 余佩倡，吴峻，周文武. 永磁同步电机矢量控制系统设计［J］.电力电子技术，2011，45(11):105－107.

［11］ 纪志成，程永奇，沈艳霞. 基于VISSIM 的永磁同步电机矢量控制系统建模与仿真［J］. 系统仿真学报，2005，17(7):1569－1576.

［12］ Mohamed Y A R I.Design and implementation of a robust current－control scheme for a PMSM vector drive with a simple adaptive disturbance observer［J］.IEEE Transactions on Industrial Electronics，2007，54(4):1981－1988.

［13］ 潘三博，陈宗祥，潘俊民.一种新型直流环节谐振逆变器的空间矢量脉宽调制方法［J］.中国电机工程学报，2007，7(1):65－69.

［14］ Wang Xudong，Mao Liangliang，Yang Shucai，et al. Application and simulation of SVPWM in three phase inverter［C］//Proceedings of the 6th International Forum on Strategic Technology.IEEE，2011:541－544.