基于声-地震动加权融合的弹丸落点定位算法

熊 超，郑 坚，张炳文，王 栋

（1.军械工程学院，河北 石家庄 050003；2.中国华阴兵器试验中心，陕西 华阴 714200）

0 引言

靶场试验或实弹演习中，弹丸落点坐标的确定是一项经常性工作。目前通常采用光学交汇的方法进行落点坐标测量，其中摄像交汇数据处理难度较高，CCD 摄像设备成本较高；指挥镜交汇难在可能漏捕，丢失数据，定位精度较低。因此，弹丸落点坐标的快速精确定位，是靶场试验中亟待解决的一个难题。近年来，声源定位的研究热点主要集中在被动声定位方法［1-3］，该方法定向精度较高，可使用双基地侧向交叉的途径实现定位，但易受环境的影响，特别是对砂弹等非爆炸性弹丸的定位误差较大，且漏测现象较为严重。为解决以上不足，本文引入地震动定位方式，提出了一种基于被动声／地震动信号探测的弹丸落点定位加权融合算法。

1 研究基础

1.1 目标地震动信号分析

基于地震动信号的目标定位方法由于受气候影响小，广泛应用于环境监控、地震探测、目标识别等方面［4-5］，在落点定位方面应用较少。弹丸落地后给了地面介质一个较大的冲击，触发爆炸产生巨大的爆炸冲击，由于两者间隔时间较短，可视为同一个震源。产生的地震弹性波主要有纵波、横波和瑞雷面波，三者皆可以作为目标定位的探测及分析对象［6］。

由于纵波和横波主要在地下介质传播，存在衰减较大的缺点。同时考虑到通用性和便携性，选取在自由表面传播的瑞雷波为探测对象，其能量强，传播距离远，更适合远距离震源探测。文献［7］表明在远离运动列车2～3km 外能够有效探测到其产生的地面振动信号，从侧面证明了冲击较大的砂弹的可探测性，为算法的可实现性奠定了理论基础。

1.2 阵列模型及其算法

目前被动声定位的研究方向主要集中在阵列技术和定向算法两个方面：文献［1-3］对阵元数目以及阵列几何结构对定位精度的影响进行了分析；文献［8-10］则主要对目前较为常用的空间几何算法和波束形成方法进行了研究。

前期研究表明：当传感器数目较少时，使用空间几何算法运算量小，计算结果准确；空间对称阵列的定位性能较好，但弹丸爆炸基本处于地平面，俯仰角可忽略，同时考虑到地震动信号为地表传播的瑞雷波，经过对比，采用五元十字面阵作为基本阵列模型；同时由于传统的单一基阵定距精度较低，无法满足定位需求，需用两个以上的传感器阵列确定目标方位角，通过平面交叉实现定位。综上所述，最终确定双五元十字面阵为定位阵列模型，如图1所示。

图1 双基阵列模型图Fig.1 The model of doubled-array

在XOY 平面内，基阵1中心传感器1位于原点O，四个探测传感器（2，3，4，5）位于坐标轴上，距原点距离均为D，基阵2的中心传感器6位于O1（r，0），阵列布置同基阵1。假定T（x，y）为落点，到原点的距离为R，连线OT 与X 轴夹角φ1 为落点方位角。目标信号到达各探测与中心传感器的时延为τ1i，距离差为d1i（i=2，3，4，5），则有：d1i=v×τ1i（v为目标信号波速），根据基阵1几何关系可得

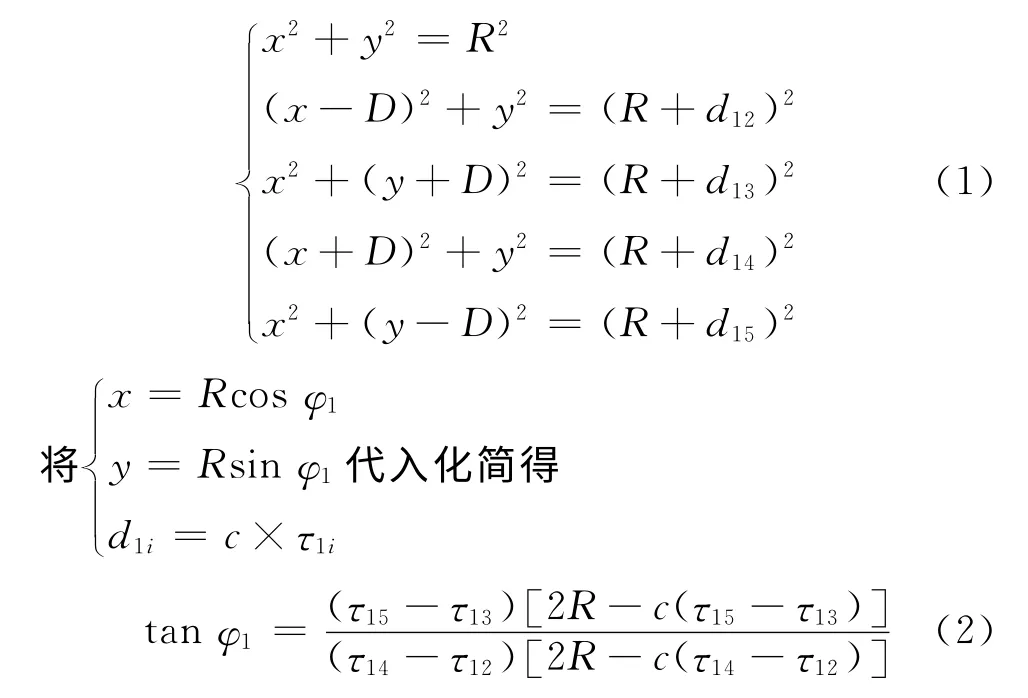
由于实际条件下R ≫c×τ1i，结合目标与基阵1几何关系，上式化简为：

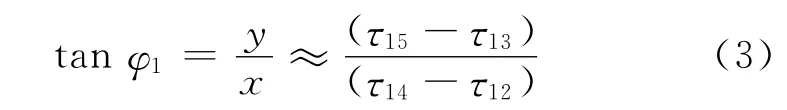
同理可得

式（4）中τ1i'为基阵2对应时延，由式（3）、（4）可得：

式（5）即为落点的坐标方程。由方程可知，通过计算各传感器之间的时延便可确定落点位置。

为保证后期结果加权处理中声信号和地震动信号具有较高的一致性，两种方式采用相同的传感器阵型。

2 加权融合算法

通过对比，选用动态加权数据融合方法中的最小方差法，在总均方误差最小这一最优条件下，根据传感器得到的测量值，以自适应方式找到其对应的权值，实现最优加权融合。

以方位角φ1 为例，设各传感器的测量方差分别为σ1，σ2，…，σN，各测量值φ11，φ12，…，φ1 N 彼此独立并且是φ1 的无偏估计，则融合值和加权因子应该满足下述关系：

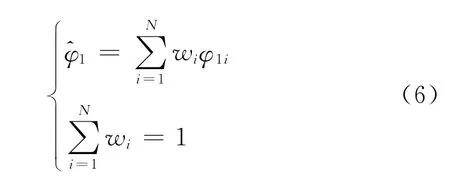
根据多元函数极值理论，可得到总均方误差最小时所对应的加权算法为：

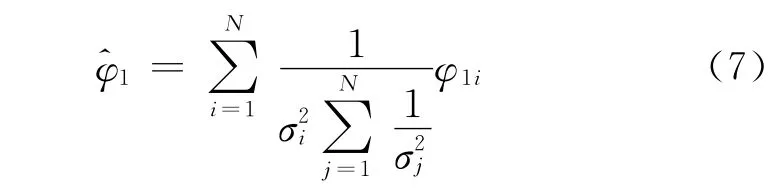
则φ^1 为对所有探测信息进行融合之后的最优方位角解，同理可得方位角φ2、坐标（x，y）的最优解。

在实际实验中，对探测到的同源信号进行相关处理，得出各路信号之间的时延估计，代入式（4）、（5），求解出单次实验的落点坐标，多次实验后取坐标的样本平均值进行均方差处理，根据加权算法进行加权，最终获得弹丸落点位置参数的最优解。

3 模拟实验

3.1 实验设计

以模拟靶场环境为前提，考虑到地震动传感器布置特性，选取空旷且平坦的室外草地进行了小型模拟实验，硬件设备构成如图2所示。使用小型炸药爆炸模拟产生爆炸波脉冲，由于爆炸源与传感器阵列距离较大，远大于爆炸源本身尺寸，因此可将其视为点状信号源，并假设爆炸声波按球面波进行传播，爆炸地震波在地表按照平面波进行传播。按图1架设传感器基阵，每个传感器阵元同时设置一个声传感器和地震动传感器，其中地震动传感器置于地表，正上方固定声传感器，高度h=0.5m，如图3所示。取阵列尺寸D=3m，基阵间距r=15m，阵元传感器布置方式如图3所示，实验点位置示意图如图4所示，在每个实验点进行了5次实验。

图2 硬件设备构成Fig.2 The composition of hardware

图3 阵元传感器布置方式Fig.3 Sensor position

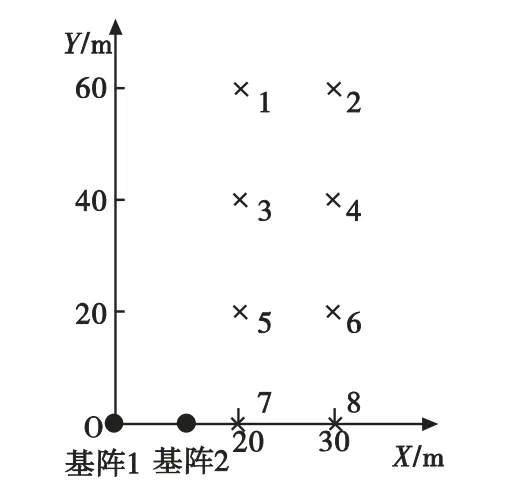
图4 炸点位置示意图Fig.4Test point distribution

3.2 实验信号分析

为分析实际实验中声信号和地震动信号的特性，验证探测方式的可行性，对室外爆炸源产生的声信号和地震动信号进行探测、采集，结合信号处理技术对实测信号进行时域和频域分析，并对三种定位方式的定位结果进行对比综合。

3.2.1 实测声信号分析

图5为单个声传感器阵列采集到的五路声源信号，皆为明显的脉冲信号，符合爆炸信号特点。五路信号除时间分布不同，波形较为相似，说明采集到有效的实验数据，探测方式可行。

图5 实测声信号时域图Fig.5 Time domain graph of actual acoustic signal

图6 为五路信号中随机取出的两路信号放大图，分析图6可知，目标信号较为纯净，为冲击脉冲的衰减过程，在爆炸声波到达前基本保持零值，到达后幅值迅速变化，并很快衰减至零，特征十分明显，信号相关性较好。

图7为五路声信号的频域图，从图中可以明显看出，同一阵列中不同传感器采集到的信号频率分布相似，主频率（峰值）所在位置相同，说明传感器阵列采集到的信号为同源信号。

图8为单路声信号频谱放大图，分析可得声信号频谱具有一定带宽，且第一路和第五路信号主频率均约为230Hz，处于声波频率范围内。

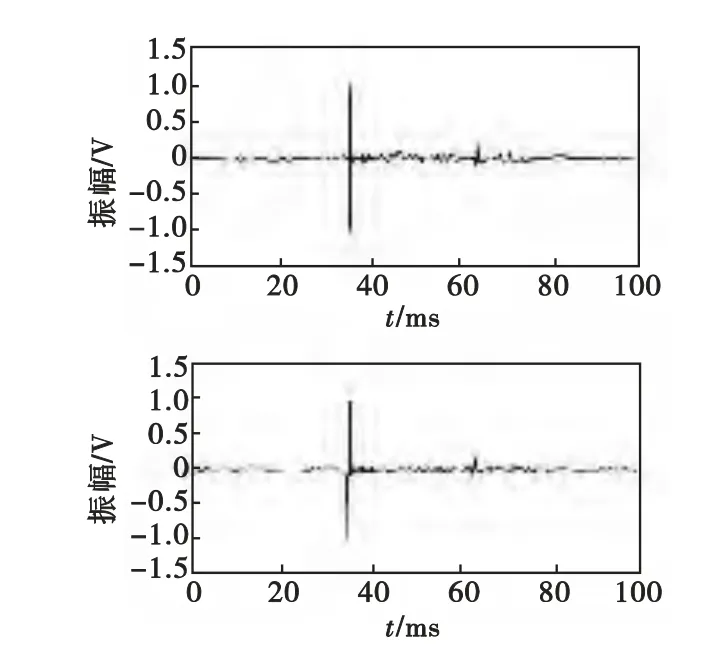
图6 单路声信号时域放大图Fig.6 Enlarged time domain graph of single channels

图7 实测声信号频域图Fig.7 Frequency spectrum of array acoustic signal

图8 单路声信号频域放大图Fig.8 Enlarged frequency spectrum of single acoustic channels

3.2.2 实测地震动信号分析

图9为同一阵列采集到的五路地震动信号，波形与声信号相比有较大不同，信号振荡过程持续时间较长，符合地震波信号特点，探测方式可行。图10为单路信号放大图，分析可知，目标信号整体为冲击脉冲的衰减过程，在首个脉冲后有较为明显的余波，随后基本以指数包络规律衰减至零。

图11为经滤波后地震动信号的频域分布图，从图中可以明显看出，同一阵列中不同传感器采集到的信号频率分布相似，主频率（峰值）所在位置相同，证明采集到的信号为同源信号。分析图12中单路地震动信号的频谱放大图可知，信号成分较为简单，第一、三路信号频率均约为7.4 Hz，由文献［11］可知，传感器采集到的信号频率处于6～10 Hz，即瑞雷波，地表传播介质为粘土，假设得到验证。

图9 实测地震动信号时域图Fig.9 Time domain graph of actual seismic signal

图10 单路地震动信号时域放大图Fig.10 Enlarged time domain graph of single channels

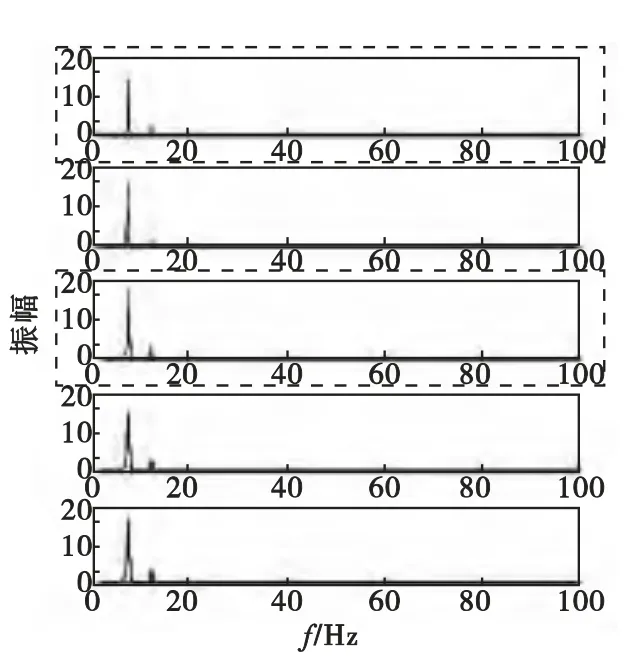
图11 实测地震动信号频域图Fig.11 Frequency spectrum of array seismic signal

3.3 定位结果分析

将模拟实验所测得的数据进行处理后，整理汇总如表1所示。

分析表1数据可得，声定位和地震动定位方式都能够较为有效地实现爆炸源定位，且声定位方式的定位精度较地震动定位方式高，进行融合处理后定位稳定性得到了提高。

为较为直观地对比这三种方式之间的差异，综合三种定位结果与原始坐标进行比较，分布图如图13所示。

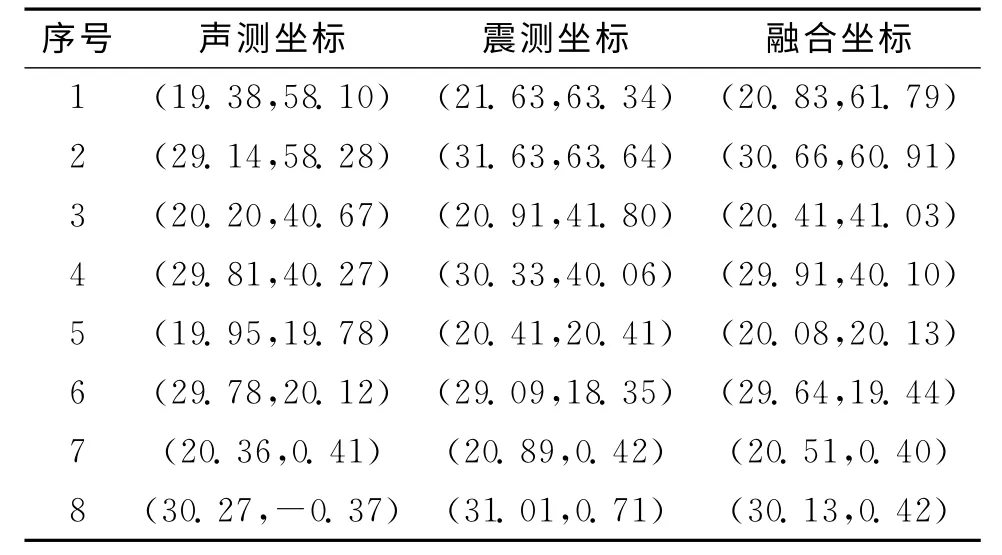
表1 定位结果对比Tab.1Comparison of locating result

由图13可得，声定位的定位精度较高，距离原始坐标的距离较近；地震动定位的结果距离远，散布较大；融合结果定位精度得到提高，散布减小。

将三种定位结果换算成定位距离，其相对误差分布如图14所示，图中数据较为明显地表现出了不同定位方式定距的相对误差分布，中间区域的误差较边缘区域要小，声定位方式精度要优于地震动定位，而融合处理进一步提高了精度，误差分布较为平缓，定位性能较为稳定，最大相对定距误差为1.41%，最小误差为0.13%。

图12 单路地震动信号频域放大图Fig.12 Enlarged frequency spectrum of single seismic channels

图13 定位结果分布图Fig.13 Distribution of locating result

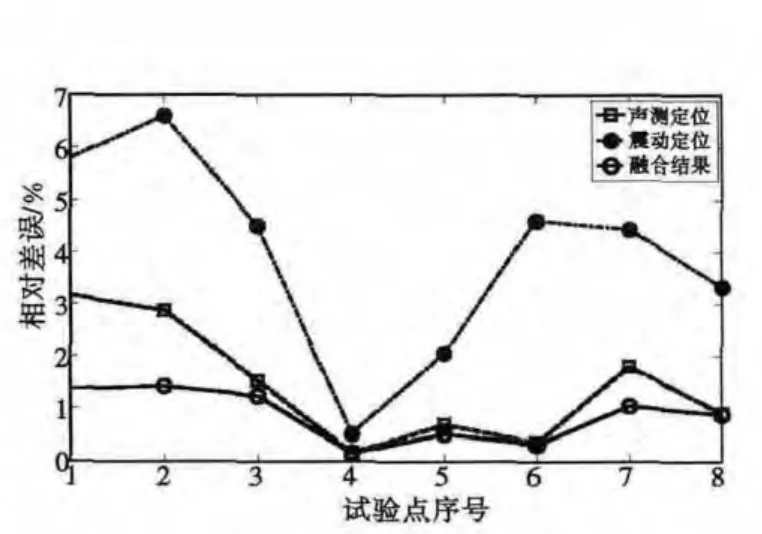
图14 定位精度对比Fig.14 Comparison of locating precision

综上可知，进行的模拟实验能够实现爆炸源的定位，探测及定位方法可行；但是由于是粗浅的定性实验，且定位算法中部分近似是依据远距离定位取得的，还需要进行进一步研究。

4 结论

提出了一种基于被动声／地震动信号探测的弹丸落点定位加权融合算法。该算法仍以相关算法为基础，通过测向交叉定位实现落点定位，引入地震动信号，并将地震动、声两种定位方式的定位结果进行动态加权融合。为验证可行性及有效性，以双五元十字面阵为阵列模型，进行模拟实验。信号分析结果和定位结果表明：传感器阵列有效探测到两种目标信号，地震动方式能够实现目标源定位，且和声定位结果加权融合后稳定性得到提高。融合定位方法可行、有效。但是由于是粗浅的定性实验，且定位算法中部分近似是依据远距离定位取得的，还需要进行进一步研究。

［1］祝龙石，庄志洪，张清泰.利用圆阵实现声目标的全空域被动定位［J］.声学学报，1999，24（2）：204-209.

［2］陈华伟，赵俊渭，郭业才.五元十字阵被动声定位算法及其性能研究［J］.探测与控制学报，2003，25（4）：11-16.

［3］林晓东，吴松林，张川.六元探测基阵被动声定位算法及其性能研究［J］.声学技术，2008，27（2）：192-196.

［4］马春庭，郑坚，陈东根，等.地面战场侦察系统多目标识别的评价指标［J］.探测与控制学报，2006，28（1）：5-9.

［5］陶小亮.基于地震动的目标识别和人员定位算法研究和实现［D］.南京：南京理工大学，2007.

［6］聂伟荣，朱继南，张元春.地震波传播理论在目标探测中的应用［J］.探测与控制学报，1999，21（4）：50-54.

［7］理理，彭文涛，李纲，等.可作为新震源的列车振动及实验研究［J］.地球物理学报，2004，47（4）：680-684.

［8］肖峰，李惠昌.声，武器和测量［M］.北京：国防工业出版社，2002.

［9］Benesty J，Chen J D，Huang Y.Time-delay estimation via linear interpolation and cross-correlation［J］.IEEE Trans.On Speech Audio Process，2004，12（5）：509-519.

［10］陈华伟，赵俊渭.声矢量传感器阵宽带相干信号子空间最优波束形成［J］.声学学报，2005，30（1）：76-82.

［11］波林格G A.爆炸振动分析［M］.刘锡荟，熊建国，译.北京：科学出版社，1975.