简支钢—混组合箱梁剪力滞效应研究

2014-01-12武彦池

山西交通科技 2014年4期

武彦池

（长安大学，陕西西安 710018）

0 引言

钢—混凝土组合箱梁是由钢箱通过剪力键与混凝土板组合而成，在外荷载作用下,组合梁除发生拉压、弯曲、剪切和扭转变形外,还发生扭转翘曲和剪力滞变形[1]。由于剪力滞现象的存在,用普通梁弯曲理论计算得到的应力与考虑剪力滞效应得出的结果有较大的出入,尤其在翼板与腹板交接处的应力相差更明显[2]。孙飞飞等[3-4]推导了考虑滑移、剪力滞后和剪切变形的钢—混凝土组合梁解析解，并通过简单的运动学假设，提出了相应的钢—混组合梁位移法单元；程海根等[2]根据组合翼板微元的变形协调条件和平衡条件，采用虚功原理得到了用级数表示的应力解；尧云涛等[1]以最小势能原理为基础，提出了一种计算精度高、计算量小的梁段单元，并推导了单元刚度矩阵、等效节点荷载列阵。本文在以上研究基础上，运用ANSYS软件建立了考虑剪力滞后、剪切变形、材料和几何非线性的钢—混凝土组合箱梁三维数值模型，分析了宽跨比对箱梁剪力滞和钢—混凝土交界面相对滑移的影响，以及滑移刚度和荷载形式对组合箱梁剪力滞效应的影响，为完善规范关于组合箱梁和类似工程剪力滞系数的计算提供参考。

1 数值模型

本文参照文献[5]中的一根2.8 m长的简支组合箱型梁，建立了考虑宽跨比、滑移刚度、剪力滞后和剪切变形的空间力学模型进行有限元分析，组合箱梁截面尺寸和计算模型如图1所示。在空间分析模型中，混凝土板采用SOLID65实体单元模拟，厚度较薄的钢箱梁采用壳单元（SHELL43）模拟，纵向钢筋采用LINK8单元模拟；文献[6]研究发现：由于剪力键受到剪切作用而变形，无论是完全抗剪连接还是部分抗剪连接，钢梁与混凝土间都存在不同程度的滑移，而ANSYS软件中COMBIN39非线性弹簧单元可以很方便地模拟界面上的剪力—滑移关系[7]。三维数值模型如图1所示。

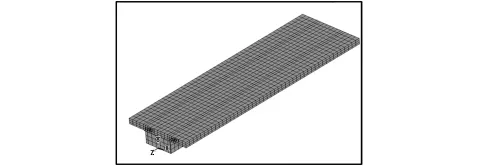
图1 组合梁截面和数值模型图

混凝土的本构关系采用应用Hongnestad建议表达式[8]：

混凝土破坏准则采用基于Willam-Warnke强度理论的五参数破坏准则，钢材的本构关系采用双线性随动强化（BKIN）模型，钢材屈服后的应力—应变关系简化为平缓的斜直线，其优点是应力—应变关系唯一，有利于收敛[9]。

模型荷载作用分为跨中集中和均布荷载，对应条件下集中和均布荷载的作用值相等。

2 剪力滞效应分析

根据钢—混凝土组合箱梁在正常使用阶段的实际工作状态，通过改变钢—混凝土组合箱梁的宽跨比、滑移刚度、荷载大小以及荷载形式等参数，分别得到相应参数变化与组合梁力学行为的变化关系。

2.1 宽跨比的影响

在分析宽跨比的影响过程中，假设在跨中横向对称集中荷载（P=30 kN）作用下，通过改变混凝土顶板宽度，使得宽跨比 r=0.3、0.4、0.5、0.6 时，钢—混凝土组合箱梁的混凝土顶板与钢箱底板的剪力滞效应及相对滑移的变化。

2.1.1 宽跨比对顶、底板剪力滞的影响

在不同宽跨比下，在混凝土顶板、钢箱底板上剪力滞系数沿跨中截面和L/4截面横向的分布规律分别见如图2和图3所示。

图2 混凝土顶板剪力滞系数横向分布图

图3 钢箱底板剪力滞系数横向分布图

由图2和图3可知，混凝土顶板和钢箱底板剪力滞系数随着宽跨比的增大而增大，即当翼缘板宽度增大时，其远离梁肋处的翼缘板因剪切扭转而发生变形，从而不参与承弯工作，靠近梁肋处受压翼缘上的压应力随着宽跨比的增大而越加明显；另外，L/4截面的剪力滞横向分布曲线明显较跨中截面平缓，说明剪力滞效应受荷载作用位置的影响，且距离荷载作用位置越近，剪力滞效应越明显。

2.1.2 宽跨比对交界面纵向滑移的影响

钢—混凝土组合箱梁的混凝土顶板和钢箱由柔性连接件连接，在外荷载作用下，其交界面不可避免会发生纵向相对错动，会直接影响钢混组合箱梁的工作，因此有必要分析宽跨比对交界面纵向滑移的影响。纵向滑移分析过程中，忽略了组合梁交界面的横向滑移，跨中集中荷载（P=30 kN）作用下宽跨比对连接件的最大相对位移的影响如图4所示。

图4 集中荷载作用下交界面纵向滑移量

由图4可以看出，在外荷载作用下钢箱和混凝土顶板并不是完全共同作用，而是两者之间存在一定的滑移，而且随着宽跨比的增大，相对滑移量也随之增大；另外，图4中的变化曲线除跨中（1.4 m）为零外，其他位置几乎呈水平状，这说明组合梁跨中位置没有发生相对滑移，其他位置的相对滑移量沿梁长变化很小。

2.2 滑移刚度对剪力滞效应的影响

通过改变非线性弹簧单元的实常数来研究弹簧剪切滑移刚度对剪力滞效应的影响，滑移刚度对钢箱底板和混凝土顶板的剪力滞效应都有不同程度的影响。由图5可知，随着滑移刚度的增大，混凝土顶板和钢梁底板的剪力滞效应都具有增大的趋势，这与文献[6]的研究结论基本一致。

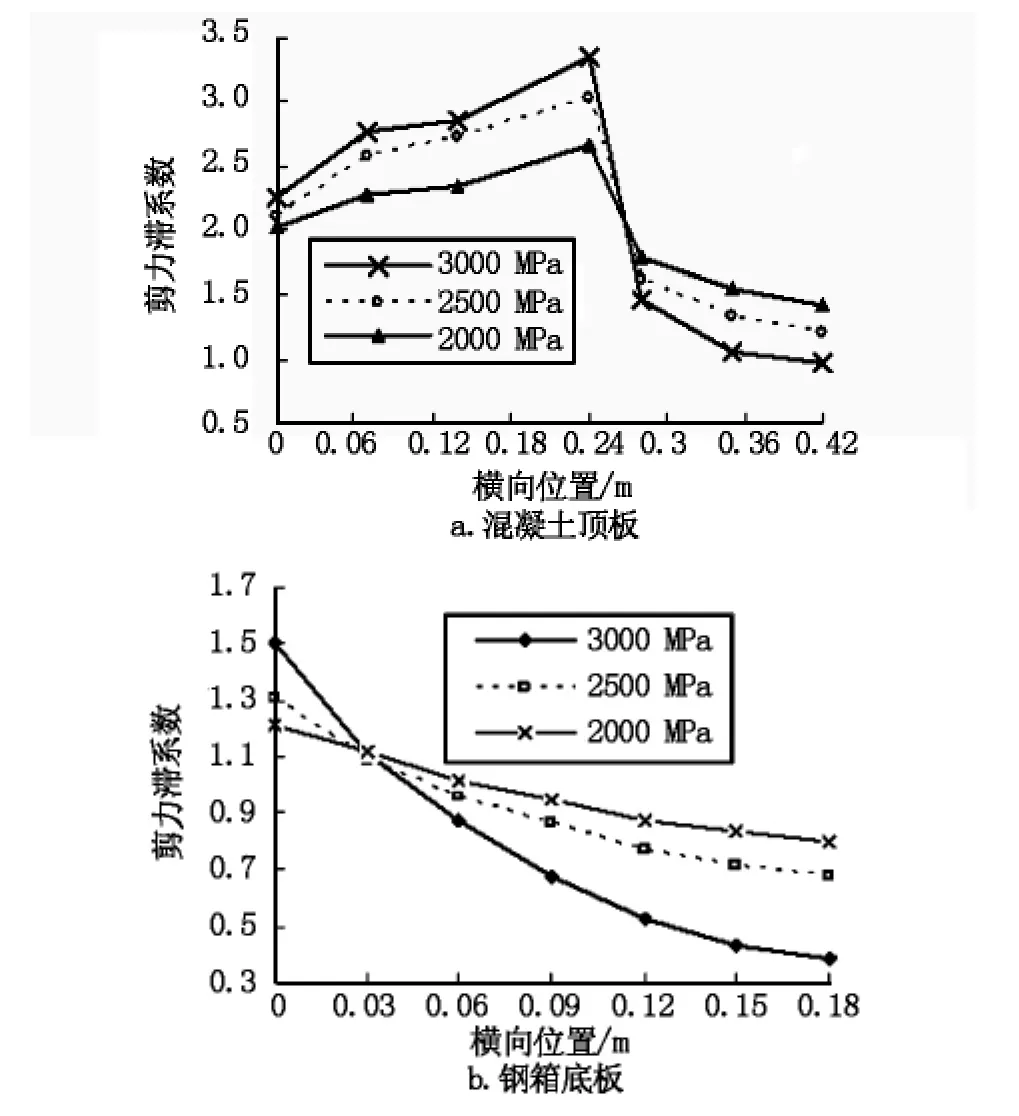
图5 集中荷载下滑移刚度对剪力滞系数的影响

2.3 荷载大小对剪力滞效应的影响

由图6可知，在竖向集中荷载作用值的大小对混凝土顶板和钢箱底板的剪应力分布影响不大，随着荷载作用的增大，混凝土板和钢底板的剪力滞系数略显增大，P=30 kN和P=90 kN作用下混凝土顶板与钢箱底板对应的剪力滞系数最大差仅为1.0%与1.6%。

图6 荷载大小对剪力滞系数的影响

2.4 荷载类型对钢混组合箱梁剪力滞效应的影响

在集中荷载（P=109 kN）和同等大小的均布荷载作用下，不同荷载类型下的剪力滞系数沿横截面和梁长方向的变化曲线如图7和图8所示。

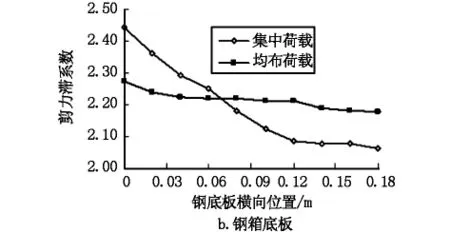
图7 不同类型荷载作用下跨中截面的剪力滞效应

根据图7可以看出，在跨中集中荷载作用下，顶板和底板靠近梁肋处的剪力滞系数大于同等大小均布荷载对应的剪力滞系数；但随着与梁肋距离的增大，底板处均布荷载对应的剪力滞系数可能会大于集中荷载作用效应。

图8 剪力滞系数沿梁纵向的变化

从图8可以看出，跨中集中和均布荷载下钢—混凝土组合箱梁的剪力滞系数沿梁长的分布规律明显不同，集中荷载作用下的最大剪力滞系数出现在作用点处，而均布荷载的则出现在支座附近；图8中a还表明，竖向集中荷载作用下剪力滞效应发生在有限的作用范围内，距离荷载作用点越近，剪力滞效应越强，且当达到距离一定程度时，剪力滞效应将趋于稳定。