预应力混凝土曲线梁桥受力性能参数化分析研究

2014-01-12李群锋

山西交通科技 2014年4期

李群锋

（山西省交通科学研究院，山西太原 030006）

0 引言

曲线梁桥作为桥梁中的重要类型，在高速公路、山区公路以及城市道路建设中，都可以看到这类桥梁的大量应用。曲线梁桥比直线桥能更好地适应路线设计要求，且具有造型优美、线形流畅、适应地形能力强等许多优点，故而在桥梁工程中获得了广泛的应用。在山西省高速公路修建过程中，除了在主线设计中会遇到曲线梁桥外，更多的曲线梁桥设计存在于互通设计过程中。一般来说，主线上的曲线梁桥由于曲率半径较大且采用预制吊装施工方法，基本上是采用“曲桥直做”的简单设计方法，而互通中的曲线梁桥因曲率半径较小且都是采用现浇施工方法，因此在理论计算和设计施工过程中都较直线桥复杂的多。

由于曲线梁桥结构在荷载作用下存在“弯扭耦合”效应[1]，因而其整体结构力学性能与直线桥有很大的不同。曲线梁桥结构的设计早期一般采用“曲梁直做”的方法，其分析方法采用直线桥分析方法。随着曲线梁桥工程实践的增加，一些国家的设计规范对曲线梁桥按直线桥分析的前提条件进行了相应的规定，如美国、加拿大、日本等国的曲线梁设计相关规定。其中，加拿大安大略省公路桥梁设计规范（简称OHBDC）中采用L2/bR＜1.0作为判别是否可以按直线梁桥计算的条件，其中L为桥梁轴线弧长，b为桥梁半宽，R为曲线梁半径。当L2/bR＜1.0时，可按直线桥计算其结构内力和变形；当L2/bR＞1.0时，则必须按曲线梁桥来进行计算与分析。另外，如果曲线梁曲线半径R＞90 m时，对于纵向弯矩的计算可近似按直线桥来考虑，但对于桥梁纵向扭矩则仍需要按曲线梁理论来进行分析。我国著名桥梁专家李国豪教授在《大曲率薄壁箱梁的扭转和弯曲》一文中指出，针对曲线箱梁曲率半径R与桥宽B的比例R/B＜10的大曲率情况，进行扭转和弯曲分析时，应考虑曲率在截面上的变化，以避免太大的误差[2]。

虽然曲线梁桥结构在桥梁工程实践中应用广泛，但针对曲线桥梁进行参数分析研究，总结不同参数变化对曲线梁桥结构力学性能的影响规律对于曲线梁桥结构设计而言是有必要的。高速公路中的曲线梁桥在实际设计中更多的是采用全部双柱墩，独柱墩曲线桥由于整体稳定性较前者差，所以较少采用。而本文就是针对高速公路互通设计中常采用的3×30跨一联的曲线梁桥来进行参数化分析研究。

1 曲线梁桥设计参数及分析模型

本文中的既有曲线梁桥跨径布置为3×30 m，桥宽12.0 m，单箱双室，主梁跨中断面尺寸见图1。主要材料设计参数为：主梁混凝土采用C50，桥面铺装为10 cm的钢纤维混凝土+10 cm沥青混凝土，防撞护栏（一侧）：10.0 kN/m；支座布置：所有桥墩均为双柱支墩，支座中心间距d=6 m。

图1 主梁跨中截面尺寸（单位：cm）

由于不同结构形式的桥梁具有不同的力学行为，必须针对性地创建其模型，选择维数最低的单元去获得预期的效果[3]。故本文采用大型有限元软件ANSYS中提供的Beam188、Beam4空间梁单元以及Mass21质点单元来建立该曲线桥梁有限元分析模型。在模型建立中，采用Beam188单元模拟主梁单元，支座处刚臂采用Beam4单元模拟，而横隔梁则采用Mass21质点单元模拟。有限元分析模型如图2所示，支座约束条件见图3。

图2 曲线梁桥空间有限元模型

图3 支座约束条件示意图

2 曲率半径对曲线梁桥受力性能的影响规律

本小节在曲线桥跨径布置为3×30 m，桥宽为12 m的前提下，分别设置曲线梁桥曲率半径R=50 m，100 m，200 m，300 m，500 m。在恒载工况（一期+二期）下，分别计算在各个曲率半径条件下曲线梁桥主梁结构关键截面位置处位移及内力，并与相同计算参数条件下直线桥的计算结果进行对比分析。经过一系列数据处理整理出曲线梁桥主梁结构关键截面位置处竖向位移Uy，弯矩My，剪力Qz以及扭矩Mx随曲率半径的变化规律分别如图4～图7所示。

图4 主梁竖向位移Uy随曲率半径变化规律

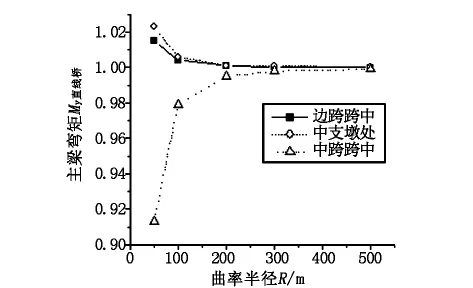
图5 主梁弯矩My随曲率半径变化规律

图6 主梁剪力Qz随曲率半径变化规律

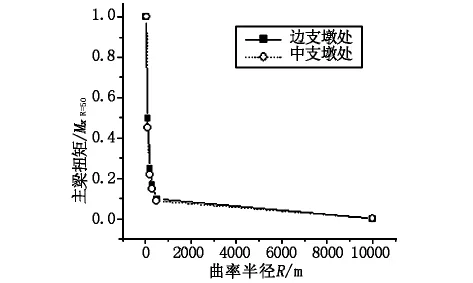
图7 主梁扭矩Mx随曲率半径变化规律

从图4～图7中可以看出：

a）随着曲率半径的增大，曲线梁桥边跨跨中竖向位移逐渐减小而中跨跨中竖向位移则逐渐增大；曲线桥弯矩变化规律为边跨跨中和中支墩处弯矩减小，中跨跨中弯矩增大；剪力变化规律为边支墩和中支墩处剪力值有小幅增长，主梁扭矩表现为边支墩和中支墩处扭矩值大幅减小直至零值。

b）对于曲线桥位移、弯矩以及剪力值，除中跨跨中位移值随曲率半径增大有25%的减小幅度外，其余变化幅度均在9%以内，尤其以剪力值变化幅度为最小。

c）曲线桥由于存在“弯扭耦合”效应，对于小曲率半径的曲线桥会在主梁截面产生较大的扭矩值，随着曲率半径的增大，扭矩值迅速减小，当为直线桥时，其扭矩值基本为零值。

d）对于3×30 m一联且桥宽为12 m的现浇曲线梁桥，综合以上位移及内力分析对比结果可以建议，当R≥300 m（即R/L≥10）时，曲线梁桥可以近似按照直线桥来进行计算分析。

3 边中跨径比对曲线梁桥受力性能的影响规律

本节在桥宽为12 m，总跨径L1+L2+L1=90 m不变的前提下，以曲率半径R=50 m的曲线梁桥为例，分别设置曲线梁桥边中跨径比L1/L2=0.5、0.6、0.7、0.8、0.9、1。在恒载工况（一期+二期）下，分别计算在各个边中跨径比条件下曲线梁桥主梁结构关键截面位置处位移及内力。最终总结出曲线梁桥主梁结构关键截面位置处竖向位移Uy，弯矩My，剪力Qz以及扭矩Mx随边中跨径比的变化规律分别如图8～图11所示。

图8 主梁竖向位移Uy随边中跨比变化规律

图9 主梁弯矩My随边中跨比变化规律

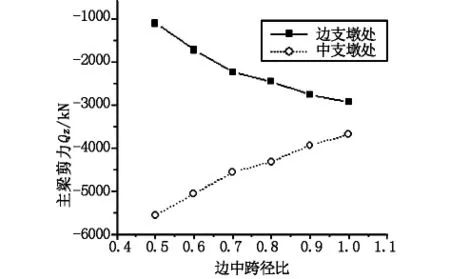
图10 主梁剪力Qz随边中跨比变化规律

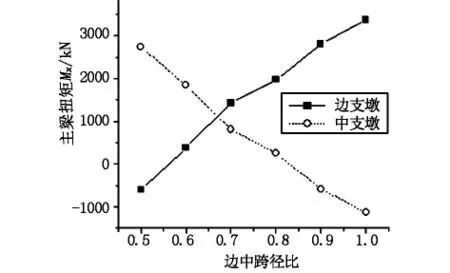
图11 主梁扭矩Mx随边中跨比变化规律

从图8～图11中可以看出：

a）随着边中跨径比的增大，边跨跨中竖向位移、弯矩逐渐增大，中跨跨中竖向位移、弯矩以及中支墩处负弯矩逐渐减小；剪力变化规律表现为边支墩剪力值减小，中支墩剪力值增大；扭矩变化趋势为边支墩从负扭矩向正扭矩增大，中支墩从正扭矩向负扭矩减小。

b）对于曲线梁桥，其位移、弯矩、剪力随边中跨径比的变化规律同直线桥，与直线桥不同的是，边中跨径比的变化还会对曲线梁桥的主梁扭矩分布产生影响。因此对于曲线梁桥来说可以通过改变边中跨径比来调整边支墩和中支墩处的扭矩值分布。

c）从边跨跨中竖向位移、弯矩和中跨跨中竖向位移、弯矩分布基本相等的角度来考虑，可以看出该曲率半径条件下的曲线梁桥最优边中跨径比L1/L2=0.85，即合理跨径布置为28+34+28=90 m。同时也可以看到在该边中跨径比条件下，无论是边支墩处还是中支墩处，其扭矩值都要比等跨径布置的曲线桥要小。所以，确定合理的边中跨径比对曲线桥的设计还是很有裨益的。