高噪声环境下基于参考影像的车载序列影像定位方法
2014-01-11季顺平
季顺平,史 云
1.武汉大学 遥感信息工程学院,湖北 武汉430079;2.中国农业科学院 农业资源与农业区划研究所,北京100081;3.东京大学 空间信息科学研究中心,东京
1 引 言
地面运动平台的精确定位是城市监控[1]、建模[2-3]、测量与识别[4]、机器人导航[5]等诸多应用的关键技术和前提条件,研究领域广泛涉及摄影测量、计算机视觉、机器人、计算机图形学等学科和专业[6]。运动平台的定位可分为动态定位(dynamic localization/real-time localization)与全局定位(global localization)。动态定位追求当前时刻载体的最佳状态,注重实时性;而全局定位则要求所有时刻状态最优,往往采用事后处理技术,精度也相对较高。视觉序列影像/绝对地理参考之组合是一种常用的全局定位方法。视觉序列影像可由安置于运动平台上的单相机、立体相机、全景相机等成像传感器获取,而地理参考,除传统的人工布设控制点(ground control points,GCP)外,还有 GPS[7-8]、地图[5]、地标、正射影像[9]等。GPS是最直接有效的手段,然而,在城区车辆定位中,峡谷效应所引起的信号遮挡和多路径问题使得GPS信号定位精度较差[9-10]。若利用正射影像作为地理参考,则需面对两个经典问题的挑战性组合:第一,参考影像与地面运动平台序列影像如何配准,属于多源异构的影像匹配问题;第二,针对大量误匹配导致的错误地理参考,如何实现定位模型的抗差解算。
多源影像匹配是一个热门的研究课题[11-13],其难点在于“变化”。对本文而言:①在辐射上,车载影像需重采样为正射投影以便匹配,高于路面的动态车辆、行人将引起几何纠正偏差,城区高建筑产生的阴影影响更大;②在几何上,根据误差传播规律,数千张车载影像序列将产生巨大的累积偏移;③在尺度上,比例尺差异导致道路的宽度在航空影像中仅占上百个像素甚至几十个像素,显然不适宜建立多层金字塔,无法采用金字塔搜索策略[14]。经统计,本文所采用的试验数据匹配错误率约80%。
定位模型的求解,通常包括3类方法:基于光线束和最小二乘的光束法平差(bundle adjustment,BA)[6,15],以运动模型和马尔可夫随机链为基础的卡尔曼滤波及扩展卡尔曼滤波(extended Kalman filtering,EKF)[16-17]和粒子滤波(particle filtering,PF)[18]。理论而言,BA 精度最高,但要求最为苛刻,需要较好的初值条件和分布良好的GCP。此外,BA常用的抗差算法,如RANSAC或选权迭代,只能处理像点坐标这类有固定几何约束(共线条件)的观测值。如选权迭代首先假定观测值符合高斯分布,然后才能由信息矩阵确定的统计量判断是否为误差。显然,匹配获取的GCP,没有固定几何约束,也不符合高斯分布;传统粗差探测算法很难有效应用于这类观测值。EKF是运动平台或序列影像定位的经典方法,相较于BA,收敛性较好;然而,它要求初始位置必须已知,并假定观测值服从高斯分布[17],因此在高噪声条件下可能产生较大的求解偏差。而PF在理论上可处理任意分布的观测值,这就决定了它可以用来模拟粗差这种无规则的概率分布。本文将以PF为理论基础,提出一种新的高噪声条件下的运动平台自动对地定位方法。
本文实现方法包括图1所示的3个关键步骤:①建立通用随机定位模型,将几何观测值、辐射观测值视作两类约束条件,并根据贝叶斯准则和马尔可夫随机场,推导出运动平台定位严格的、通用的统计模型;②多源影像匹配,以获取(高噪声)的GCP观测值,首先完成全景序列影像自身的匹配和模型连接,然后将其正射重采样以利于匹配,再通过采样后的全景影像与正射影像的多重假设相关,获得多个候选GCP;③求解策略,基于粒子滤波原理,提出蒙特卡罗匹配与定位算法(Monte-Carlo georegistrationmethod,MCG),通过一系列“预测、更新”,实现高噪声条件下的运动平台精确定位。

图1 基于参考影像的运动平台定位模型与求解方法总体流程Fig.1 The probabilistic localization model and MCG method based on geo-referenced image
选择PF的意义在于其不需要观测值的正态分布假设,粒子的多样性,恰可对应大量误匹配、多峰值所所导致的任意分布的GCP。迄今,PF常被用作EKF的替代品,它在高噪声观测条件下的表现,还未被强调。将PF首次引入到高噪声、无模型约束观测数据的处理中,验证其强大的抗差能力,实现车载序列影像的精确定位,是本文的主要贡献。
2 方 法
2.1 基于贝叶斯和马尔科夫链的运动平台通用定位模型
设St为1∶t时刻所有已拍摄运动平台影像序列与参考影像之间的物理或辐射约束的集合,通常表达为特征间的相似度;Gt为1∶t所有的几何约束,在序列影像定位中通常由相邻帧之间的运动模型表达;Lt为1∶t时刻影像序列的位置和姿态,即待求模型参量;St、Gt表示当前帧的辐射约束和几何约束,Lt是当前帧的位置和姿态。全局定位问题即在这两类约束条件下,使得下列条件概率达到最大

而实时定位中一般考虑当前状态最优

本文着重考虑全局定位问题。假定运动轨迹符合一阶马尔可夫链,对式(1)进行进一步推导。将式(1)写作信度Bel(Lt),根据贝叶斯准则可得

在式(3)中,η=p(St|St-1,Gt)-1,为归一化常量。由于各特征间的辐射约束相互独立,条件St-1可省略;且根据马尔可夫特性,在Lt已知的前提下,St独立于之前的状态Lt-1,则式(3)进一步简化为

式(4)的最右式同样可以进一步由贝叶斯准则因式化,得到

由于当前的几何约束Gt无法影响之前的位置Lt-1,且根据马尔可夫链,Lt只与Lt-1相关而与之前的状态无关,则式(5)可以进一步简化为式(6),并可写作式(7)的递归形式
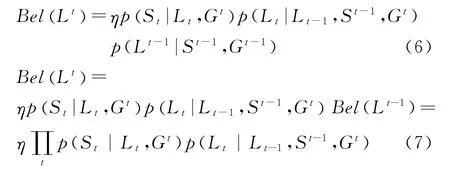
在观测值独立与运动平台符合马尔可夫随机场的宽假设下,式(7)是序列影像全局定位问题通用的、严格的统计模型且并不要求观测值符合高斯分布。至于两类约束条件,并不局限于辐射和几何,可根据实际应用替换为特定的形式,亦可导出不同的求解方法。如将p(St|Lt,Gt)视作共线条件的后验概率,p(Lt|Lt-1,St-1,Gt)为IMU测定的运动模型后验概率,通过对式(7)取-log并求其极小值,则可导出一种光束法平差方法RBA(relative bundle adjustment)[19];类似的,将p(Lt|Lt-1,St-1,Gt)视作预测方程,将p(St|Lt,Gt)视作更新方程,则导出EKF、PF[20]。
2.2 多源影像匹配
2.2.1 全景序列影像匹配
为求解式(7),首先需要根据特定的问题,赋予后验概率p(St|Lt,Gt)和p(Lt|Lt-1,St-1,Gt)恰当的闭合形式。对于本文而言,将通过两类匹配——全景序列影像匹配和多源影像匹配,对两个后验概率赋值。
首先,p(Lt|Lt-1,St-1,Gt)描述前一时刻位置及两类约束条件已知的前提下,当前位置Lt的概率分布。由于Lt-1已知,可直接忽略辐射约束St-1、Gt-1;故该条件分布变成广为所知的运动模型p(Lt|Lt-1,Gt),其参数可由陀螺数据积分或视觉测程(visual odometry,VO)获得。本文采用球面投影的全景视觉测程获取Gt,计算方法近似于摄影测量中的相对定向。全景成像模型与传统平面相机有一定区别,每一个像点都必须采用三维坐标表示,z坐标互不相同。然而,所有的光束依然满足共线条件,因此共面条件依旧可表达为

式中,B、R、V1和V2分别代表基线、旋转矩阵、左右影像的同名像点坐标向量。细节部分可参考文献[8,21]。在B、R已知时,运动模型可被线性化为

由于临近帧间的相对定向精度较高,可进一步认为运动模型符合高斯分布

式中,l是当前位置的期望,由式(9)获得;δ是均方差,由相对定向的解算精度决定。在某些情况下,运动模型并非在相邻帧之间建立,如本文考虑到道路宽度(约10m)和相邻影像间隔(1m),采用10张影像作为一个整体block,则运动模型可由block局部平差获取的位置和精度确定。
全景序列影像定向的具体流程如下:①在全景相机的独立鱼眼镜头上提取三度重叠以上的SIFT特征点并进行匹配[21];②剩余的同名特征转换到全景坐标系下并代入到式(8),引入RANSAC剔除粗差;③每10张影像进行BA,以提高定位精度及后继重采样的质量;④将连续相对定向后的第一张影像大致固定到绝对坐标系中,获得整个影像序列在绝对参考中的位置[8,22]。
为便于匹配,进一步将全景影像采样为近似正射影像。利用全景几何成像模型[8]及每幅影像的方位参数并假定地面水平,对单幅影像进行正射重采样。同时,每10张影像进行拼接,获得约10m×10m的伪正射影像。此时,纠正后的全景影像的投影方式与正射影像一致。然而,从图3(a)、图3(b)中可看出,受到光照、阴影和动态汽车影响,纠正影像质量较差,将给后续的多源影像匹配带来极大困难。
2.2.2 多源影像匹配
后验概率p(St|Lt,Gt)表达给定位置的匹配可能性。在Lt已知时,Gt显然可被忽略。Lt是搜索区间的中心,直接决定着匹配结果。受误差传播率影响,全局搜索要求搜索区间必须不断增加而导致匹配成功率迅速下降故采取边预测边匹配的迭代策略。第1步,根据运动模型式(10)和t-1时刻平台的位置,预测当前时刻t的位置。如果t-1时刻的信息正确,则只需要搜索很小的区域。第2步,通过多源影像匹配获得GCP观测值。采用多重假设的灰度相关算法,在搜索区间内匹配出一系列候选GCP。顾及高噪声条件下的匹配中的多峰值、误匹配、无匹配,保留尽可能多的峰值,即设定一个较小的匹配阈值,所有高于该阈值的相关系数所对应的位置都视作有效候选点。简便起见,假定GCP观测值服从多重假设下的混合高斯分布

式中,si指第i个候选点的相关系数或相关系数的函数,其大小表达了该候选点的“可能性”;σi是对应的方差,并没有实际意义。只关注峰值si,认为单个峰值附近的分布是“高斯的”只是为了描述方便。在高噪声环境下,匹配结果可能:最大峰值并非正确、所有峰值都错误、不存在峰值。因此,通过匹配获得的GCP,将是一个充满粗差的集合。
在获得了两个后验概率的闭合形式后,剩下的问题是如何根据式(10)、式(11)来求解通用定位模型式(7),同时需要着重考虑如何从含噪GCP中识别正确的参考信息并最佳地平衡运动模型式(10)和GCP式(11)之间的力量和权值。将在2.3节引入一种改进的蒙特卡罗算法实现高噪声环境下定位模型的求解。
2.3 蒙特卡罗匹配与定位算法(MCG)
本文的解法基于一种经典的蒙特卡罗定位方法(Monte-Carlo localization,MCL)[23],它并不直接解算式(7)中的后验分布Bel(Lt),而是将其表达为一系列随机带权粒子的集合,其权对应目标的后验概率分布密度。在式(12)中,lt,[i]={li1,li2,…,lit}是第i个粒子1∶t时刻的估计路径,其权wt,[i]确定了该粒子的重要性

将连续的后验分布离散化后,定位问题从求解式(7)演变成求解式(12),即发现一条1∶t时刻最优的、对应着最大权值的粒子路径。粒子的多样性不要求观测值是“高斯的”,它可模拟任意分布的含噪数据,即与式(11)很好地对应。具体的,将每次匹配获得的峰值位置看作是第i个粒子的当前位置,将相关系数看作是第i个粒子权值。然后,用粒子多样性针对高误匹配率,实现辐射、几何约束下的匹配、定位一体化最优解法MCG。
MCG是一个迭代的算法,主要步骤包括初始化、预测、更新、重采样:
(1)在迭代之前需要为t0时刻的系统状态初始化。若平台初始位置已知,可根据定位精度,按照高斯分布对Bel(L0)进行粒子化。若平台位置未知,即无先验信息,可根据均匀分布设定搜索区间内的粒子,权值都等于1/m。
(2)在预测阶段,每一粒子根据t-1时刻的位置和运动模型预测当前t时刻的位置li。这是一个采样的过程,即li=l+δi。l由式(9)算出,δi从高斯分布N(0,δ)中采样获得。在传统的MCL中,运动模型的精度δ由陀螺的物理精度或相对定向的解算精度确定。这个“精度”是有前提的,即认为上一次更新是正确的。而在高噪声环境下,上次或前面数次更新都可能是错误的。提出对传统MCL的第1个改进,根据观测值的信噪比和假设检验,设定运动模型的实际精度δ,详见3.4节。
(3)在更新阶段,采用多重假设相关表达辐射相似性,以li为中心搜索相关峰值s及相应的新位置l′。由于已经将总搜索区间用足够数量的粒子代替,在每个粒子的搜索范围内,只提取一个峰值。如设定100个粒子,则逐一匹配出100个候选点。从递归式(7)可以看出,权值wi等于ηp(St|Lt,Gt),而η是常数,p(St|Lt,Gt)由相关峰值s表达,则wi=s。然而,这里多源影像匹配获得的s是非常不可靠的。在这里本文提出对MCL的第2点改进,将匹配结果反作用于粒子。用p(l′|li)表达匹配结果与运动模型的关系,两者越接近,正确匹配的可能性越高,反之越低。此时,wi~p(l′|li)s。p(l′|li)设定为一个较平坦的高斯分布,使得每步迭代不至于过分向运动模型倾斜而降低粒子的多样性。
(4)在随机采样阶段,根据每个粒子的归一化权wi进行随机抽取,如10个粒子的集合,权重为0.3的粒子有很大可能被抽到3次。采样后每个粒子权值重新设定为均匀分布。经过一系列递推,粒子可能损失其多样性,即个别粒子占据非常大的权重而其他粒子被忽略。此时需在采样步骤中加入“重采样(importance re-sampling)”,再次实现粒子的多样化。在本文的定位问题中,当某个粒子的权大于一定的阈值,再次将搜索空间扩大,对粒子重新洗牌。此外,由于匹配出的“粒子”高度不可靠且所有的匹配峰值都可能错误,提出对MCL的第3点改进:为那些本该被丢弃的匹配失败的粒子,设定一个小的权值0.1,保留它们获选的可能性,从而增加粒子多样性。
图2显示了前两幅影像的MCG算法流程。第1幅影像初始位置未知,粒子设定为均匀分布。例如,常用的GPS,初始静态时精度在5m之内,初始搜索范围为100m2。第1幅中4个粒子的权值均为0.25,每个粒子的搜索半径为5m。第2幅示意了匹配后被更新的每个粒子的位置及权重,颜色的深浅代表相关系数的大小。如果相关系数小于阈值,即匹配失败,如1号点。此时为其设置一个小权值0.1保证高噪声环境下粒子的多样性。第3幅是采样步骤。1号粒子未被抽到而高相关系数的4号点被抽到2次,重采样后粒子的权值重置为0.25。第4幅包括两步:首先,根据第2步预测第2张影像的粒子;然后同第2幅图,匹配并更新每个粒子的位置及权重。
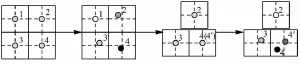
图2 MCG前两张影像算法流程Fig.2 The MCG of first two images
3 试验和分析
3.1 试验设计
为验证本文方法的在复杂环境下的可行性,选择了一段2.2km长的车辆多、遮蔽多、阴影范围大的困难路段进行试验。通过隔米曝光,共获取2410张全景影像,首先采用视觉测程方法进行影像关联[8]。图4中的黄线示意了定位结果,左下为起点,左中为终点;误差随时间累积,逐渐偏离道路。然后,对全景影像进行正射投影重采样和拼接,生成伪正射影像241张,图3(a)、图3(b)示意了其中的两张,影像图3(a)存在高于地面的汽车,重采样后影像明显扭曲和像素缺失。影像图3(b)位于天桥的阴影下,不利于匹配。采用的已知地理参考信息为一幅航空正射影像,像元分辨率0.12m,定位精度约0.25m。图3(c)为其中的一段路面,与图3(b)是对应区域。参考影像也受到运动车辆、不同时刻建筑物阴影的影响,不利于两者的匹配。同时,由车载高精度IMU联合GPS数据精确获取了影像曝光位置,用于结果检验。IMU/GPS定位精度优于0.1m。
3.2 试验结果
根据2.3节的MCG算法,获得图4中红线显示的采用100个粒子的定位结果,可见路线已被精确地修正回道路上。表1为利用241个IMU/GPS测定值(图4中蓝线)进行全路径定位精度检查的结果,平面定位精度0.57m,最大误差14.31m。而纯粹采用视觉测程方法(黄线)定位精度较低,平均定位精度82.37m,最大定位误差167.88m。由于大量的同名特征缺失加上多峰值和误匹配,使得全局BA解算失败。

表1 定位精度检验Tab.1 Check of the localization accuracy
图4的放大区域显示了路线的最后一段。该区域完全被阴影遮挡,无法匹配以获取正确的GCP。故MCG算法的定位结果与参考路线发生了一定的偏差。表1中MCG(truncated)是指去除该阴影路段后的定位结果。可见定位精度得到了进一步提高,平面精度达到0.45m,鉴于参考影像的定位精度才0.25m,因此MCG算法能够接近密集布点的BA的定位精度水平。同时最大定位误差也从14.31m减小到4.20m。
进一步分析多源影像匹配结果,即所有匹配获得的GCP的概率分布。图5显示所有241个时刻匹配峰值高于阈值0.3的GCP数量。上方的黑线代表同一个位置的粒子也被计算,此时平均候选GCP数量是49.3。如果同一位置的粒子只被计算一次,候选GCP的数量是8.5(下方的灰线)。该值表明多重假设匹配非常频繁地发生。即使认为在8.5个GCP中必然有正确的一个,那么其余7.5个粗差导致误匹配率也超过80%。这表明BA、EKF所要求的单峰值高斯分布观测值是不现实的,因此这些解法不可能成功。
恰恰相反,蒙特卡罗方法借助粒子的多样性,可模拟任意的多重假设分布,更加适用于高噪声条件下的定位问题。当然,在高噪声中,好的粒子表现突出,有助于寻找到最佳的路径,这部分取决于匹配阈值的选择。选择阈值0.3,保证绝大部分正射纠正影像块都有候选点,并且候选点在同一位置平均重复6次。这保证那些高重复率的好粒子将获得更高的权值而存活。笔者也尝试了其他的阈值。如取0.4时,有效GCP数量下降,但同时定位精度也下降,因为20%的纠正影像块找不到同名特征。需要指出的是在本文的算例中,所有241×100次匹配的最大相关系数仅0.6。
虽然蒙特卡罗在高噪声环境下表现突出,但它也有自身的缺陷。最主要的问题是由连续的概率分布离散化而引起的信息损失。对本文而言,损失一个正确匹配点,将导致该时刻节点偏离正确的路径。这是蒙特卡罗精度略低于强控制条件BA的主要原因。图6中蓝线为最优粒子路径,红圈是匹配失败的粒子,绿圈是匹配成功粒子。图6(a)为图4下方的大面积阴影区域,导致路径偏移误差;图6(b)为图4右侧区域,条件良好时的路径(为方便显示右旋90°)。如图6(a)所示,大面积阴影导致很长的区域没有正确匹配点,全区最大定位误差4.2m也出现在该区域;相反的,在图6(b)的良好条件下路径是非常正确的。蒙特卡罗自身无法修正类似图6(a)的偏离,因为它是马尔科夫的、向前的,没有向回走的机制。尽管如此,它的最大贡献是在高噪声环境下能够将错误信息产生的gaps桥接和修补,而其他方法却被错误信息困扰而解算失败。而且,若额外引入一些局部平滑算法,这些桥接误差是可能被修正的。
3.3 MCG的参数敏感性
蒙特卡罗方法的优点之一是参数少,且对参数并不敏感,这是结果稳定性可靠保证。在本文的MCG中,除了已经分析的相关系数阈值,只含两个关键参数:粒子数目和运动模型精度δ。
在较好的环境下,甚至一个粒子也能取得很好的定位精度[20]。但对于本文复杂的城区街道环境,更多的粒子数量具有更强的抗差特性和更广的拉入范围,有助于保证算法的正确收敛。图7是不同粒子数量的MCG定位结果。如图所示,粒子数量较少时,会产生较大的定位误差。如粒子数为16时(绿线),在左上角第3个拐弯处发生偏差;粒子数为32时(红线),在第4个拐弯处定位失败。而当粒子数量进一步增加,则都能收敛到正确的位置。粉、蓝、黄线分布对应粒子数64、100、150,除了终点处的阴影区域,三线几乎完全重合,定位结果差异很小。鉴于在拐弯处会产生更大的不确定性,可考虑自适应地加入粒子数量。
在传统的MCL中,运动模型的精度可根据陀螺仪物理精度或相对定向精度设定。本文以10张影像作为一个block进行光束法平差,也可根据平差的信息矩阵直接计算出运动模型精度δ0。如果上个时刻更新正确,采用δ0是毫无问题的。不幸的是由于大量误匹配,若上一次的更新错误,此时运动模型的精度可能是2δ0(简便起见,认为各block平差精度相同)。因此,δ是由最近的一次正确更新所决定,选择简单的假设检验以计算δ

式中,A和C代表误匹配率和置信水平。如果A取0.8,C取0.9,则抽样次数k等于10。这意味着每抽10次,有可能以90%的置信度从粗差为80%的观测数据中抽到一次正确的更新。试验中,δ0等于0.22m,因此δ=kδ0=2.20m(11像素)。图8显示了更为细致的结果:如果δ过小,不能容忍大量的粗差,精度急剧下降;如果δ过大,过分的离散化样本空间也将降低定位精度;当δ∈(6,15),本试验能够得到最好的定位结果。
4 结 论
城区街道布设密集的人工控制点难以实行,采用已知地理参考影像提高载体定位精度是快捷有效的手段,但高噪声环境下的多源影像匹配难以获得可靠的GCP。本文研究了高噪声GCP条件下车载序列影像的定位问题。首先从理论上推导了两类约束条件下序列影像的匹配与定位一体化严格统计模型,然后采用改进的蒙特卡罗算法MCG进行模型求解。MCG算法中粒子的多样性,保证大量误匹配发生时,仍然有粒子处于正确或接近正确的轨迹上,并获得接近于传统密集布点的BA精度。本文首次验证了即使观测值中粗差超过80%,蒙特卡罗方法仍具备强大的抗差能力,而传统的EKF、BA则难以做到。

图4 不同算法的定位结果Fig.4 Geo-referencing results of different algorithms

图5 多源影像多峰值匹配Fig.5 Multi-source multi-peak matching

图6 MCG局部图Fig.6 Part of MCG results
图7 不同粒子数量对定位结果的影响Fig.7 The geo-referencing results using different particle number

图8 定位精度随δ发生的变化Fig.8 Changes in localization errors with differentδ
[1] SCHINDLER K,ESS A,LEIBE B,et al.Automatic Detection and Tracking of Pedestrians from a Moving Stereo Rig [J].ISPRS Journal of Photogrammetry and Remote Sensing,2010,65:523-537.
[2] MEI C,BENHIMANE S,MALIS E,et al.Efficient Homography-based Tracking and 3-D Reconstruction for Single-viewpoint Sensors [J].IEEE Transactions on Robotics,2008,24(6):1352-1364.
[3] AGARWAL S,SNAVELY N,SIMON I,et al.Building Rome in a Day[C]∥Proceedings of the 2009IEEE International Conference on Computer Vision,2009,doi:10.1145/2001269.2001293.
[4] BAHMAN S,NICOLAS P,BRUNO V.Detection and 3DReconstruction of Traffic Signs from Multiple View Color Images[J].ISPRS Journal of Photogrammetry and Remote Sensing,2013,77:1-20.
[5] NAJJAR M E,BONNIFAIT P.A Road-matching Method for Precise Vehicle Localization Using Belief Theory and Kalman Filtering[J].Autonomous Robots Journal,2005,17(3):173-191.
[6] THRUN S,MONTEMERLO M.The Graph SLAM Algorithm with Applications to Large-scale Mapping of Urban Structures[J].The International Journal of Robotics Research,2006,25(5-6):403-429.
[7] DUSHA D,MEJIAS L.Error Analysis and Attitude Observability of a Monocular GPS/Visual Odometry Integrated Navigation Filter [J].The International Journal of Robotics Research,2012,31(6):714-737.
[8] SHI Y,JI S,SHI Z,et al.GPS-Supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments[J].Sensors,2012,13(1):119-136.
[9] ALONSO I,LLORCA D,GAVILÁN M,et al.Accurate Global Localization Using Visual Odometry and Digital Maps on Urban Environments[J].IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4):1535-1545.
[10] CUI Y,SAM S.Autonomous Vehicle Positioning with GPS in Urban Canyon Environments[J].IEEE Transactions on Robotics and Automation,2003,19(1):15-25.
[11] LI Zhuang,LEI Zhihui,YU Qifeng.Matching Multi-sensor Images Based on Gradient Radius Angle Pyramid Histogram[J].Acta Geodaetica et Cartographica Sinica,2011,40(3):318-325.(李壮,雷志辉,于起峰.基于梯度径向夹角直方图的异源图像匹配 [J].测绘学报,2011,40(3):318-325.)
[12] CHENG Chunquan.Research on Combined Positioning Model of Multi-source Heterogeneous Image[J].Acta Geodaetica et Cartographica Sinica,2012,41(4):622-628.(程春泉.多源异构遥感影像联合定位模型研究[J].测绘学报,2012,41(4):622-628.)
[13] JI S,ZHANG T,GUAN Q,et al.Nonlinear Intensity Difference Correlation for Multi-temporal Remote Sensing Images [J].International Journal of Applied Earth Observation and Geoinformation,2013,21:436-443.
[14] YUAN Xiuxiao,MING Yang.POS-supported Matching Method for Aerial Images between Neighboring Strips[J].Acta Geodaetica et Cartographica Sinica,2010,39(2):138-145.(袁修孝,明洋.POS辅助航带间航摄影像的自动转点[J].测绘学报,2010,39(2):138-145.)
[15] LI Deren,ZHENG Zhaobao.Analytical Photogrammetry[M].Beijing:Surveying and Mapping Press,1992.(李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992.)
[16] CESAR B,YUICHI M.Improving Estimation of Vehicle’s Trajectory Using the Latest Global Positioning System with Kalman Filtering[J].IEEE Transactions on Instrumentation and Measurement,2011,60(2):3747-3755.
[17] TAYLOR R,DOLLOFF T,BOWER M,et al.Automated Video Georegistration at Real-time Rate[C]∥Proceedings of the ASPRS Annual Conference.[S.l.]:ASPRS,2010.
[18] MADDERN W,MILFORD M,WYETH G.CAT-SLAM:Probabilistic Localization and Mapping Using a Continuous Appearance-based Trajectory [J].The International Journal of Robotics Research,2012,31(4):429-451.
[19] SIBLEY D,MEI C.Adaptive Relative Bundle Adjustment[J].Robotics:Science and Systems,2012,220:1-8.
[20] MONTEMERLO M.Fastslam:A Factored Solution to the Simultaneous Localization and Mapping Problem with Unknown Data Association[D].Pittsburgh:Carnegie Mellon University,2003.
[21] LOWE D G.Distinctive Image Features from Scale-invariant Keypoints [J].International Journal of Computer Vision,2004,60(2):91-110.
[22] JI Shunping,SHI Yun.Im age Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J].Acta Geodaetica et Cartographica Sinica,2013,42(1):94-100.(季顺平,史云.车载全景相机的影像匹配和光束法平差[J].测绘学报,2013,42(1):94-100.)
[23] THRUN S,FOX D,BURGARD W,et al.Robust Monte Carlo Localization for Mobile Robots [J]. Artificial Intelligence,2001,128(1):99-141.
