浅谈斜交桥盖梁坡度的问题

李红兵

（郑州市市政工程勘测设计研究院，河南郑州 450046）

0 前言

在桥梁工程设计中，经常会遇到桥梁斜交的情况，横坡为i%，纵坡为j%，斜交角为α，见图1。

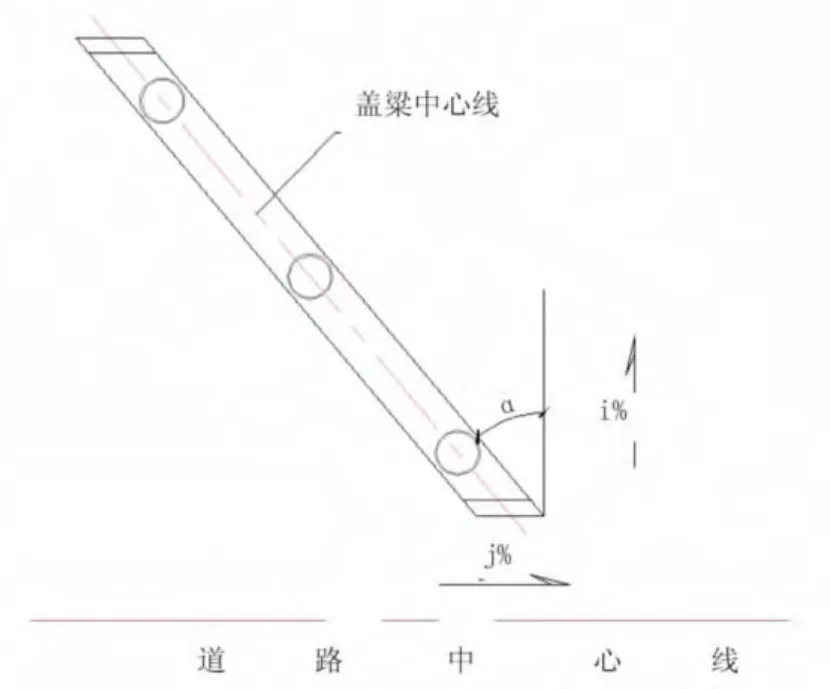
图1 盖梁中心线与道路中心线斜交示意图

这时，一般思路是，求出同一盖梁下某根柱（桩）对应的中心桩号，通过纵坡j%来求出该桩号的中心桥面标高，然后通过横坡i%来求出该柱（桩）的实际桥面标高，再减去铺装厚度、梁高、支座及垫石、盖梁高得出柱（桩）顶标高。同理，求出另一根柱（桩）的标高。最后根据两个柱（桩）顶标高及两柱（桩）间的距离推算出盖梁坡度。更有不胜其烦者，会推算出同一盖梁下的所有柱（桩）顶标高，以至于盖梁在竖直面上是一条弯折线。

上述方法不仅设计起来麻烦，施工时也很麻烦。下面根据简单推导来得出斜交桥盖梁实际坡度的公式。

1 公式推导

（1）盖梁在道路中心线上的投影范围内纵坡不变。

首先建立斜坐标系。x 轴沿道路中心线，y 轴沿盖梁中心线，z 轴垂直桥面向上。x 轴与y 轴角度等于90 °-α，x 轴与z 轴角度等于90 °，y 轴与z 轴角度等于90°，见图2。

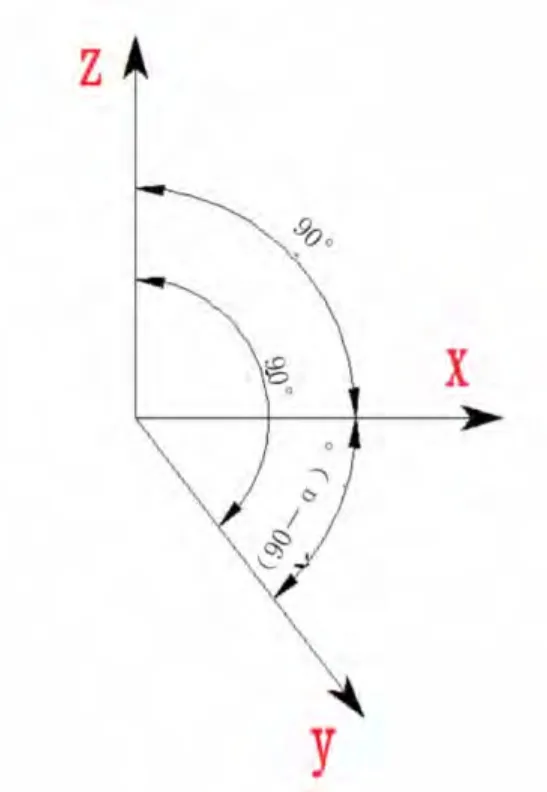
图2 根据斜交盖梁建立的三维斜坐标系

在 x -z 平面内，Δzx=Δx ×j

在 x -y 平面内，Δx=Δy ×sinα

代入得到 Δ zx=Δy×sinα×j

在 y -z 平面内，Δzy=Δy ×cosα×i

由于Δzx与Δzy 均为同轴内，可以直接作加减法，则

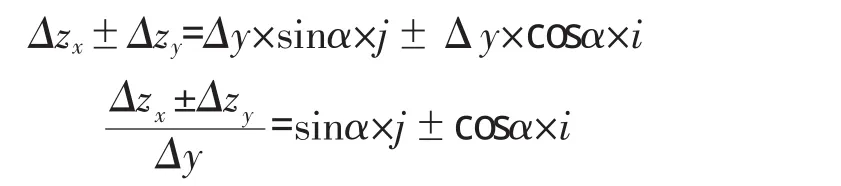
上式左边的分子为高差，分母为沿盖梁中心线距离，相除即为盖梁的实际坡度，以k 表示，得

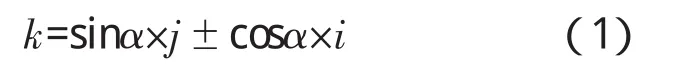
式中：k——盖梁的实际坡度；

α——桥梁斜交角；

j——道路中心线的纵坡；

i——桥面横坡。

符号规定：沿盖梁方向，i，j 符号相同为 +，i，j符号相反为-。

从式（1）中可以看出，盖梁的实际坡度在横坡i 及纵坡j 不变的情况下是一个定值。但在实际工程中，路线设计时经常把变坡点设置在桥梁范围内，特别是一些中小桥，这样盖梁在道路中心线上的投影范围内纵坡j 就不是一个定值，显然式（1）也不能简单应用于计算此类情况下盖梁的实际坡度。

（2）盖梁在道路中心线上的投影在竖曲线范围内（见图3）。

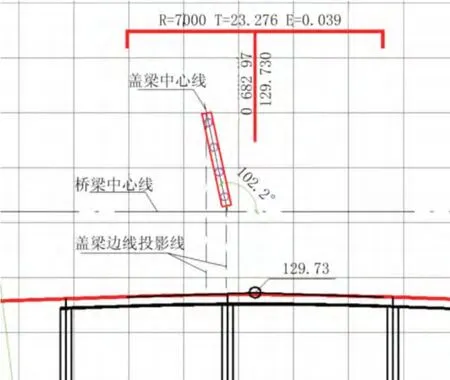
图3 盖梁在道路中心线上的投影在竖曲线范围内示意图

假设竖曲线两边坡度分别为j1%、j2%，圆曲线半径为R，坡度线1 的竖直角为，竖曲线上任意一点x 的切线与坡度线1 之间的夹角为，见图4。

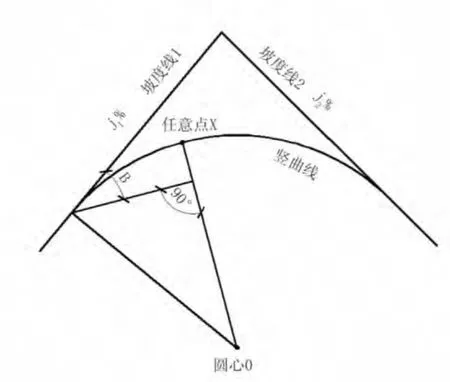
图4 竖曲线上任意点几何示意图

tanγ=j1%，由于城市道路设计规范要求最大纵坡一般不大于4%，即j1%＜0.04，根据高等数学里微分的近似公式，当 γ 非常小时，tanγ=γ，即 γ =j1。

设定盖梁两端对应道路中心桩号距竖曲线起点桩号分别为x1，x（2小注：根据几何求解，在x1，x2相对曲线半径R 不在一个量级且纵坡j 非常小的前提下，x1，x2可近似等于在竖曲线上距竖曲线起（终）点的弧长。）则盖梁两端的实际坡度分别为k1，k2得：

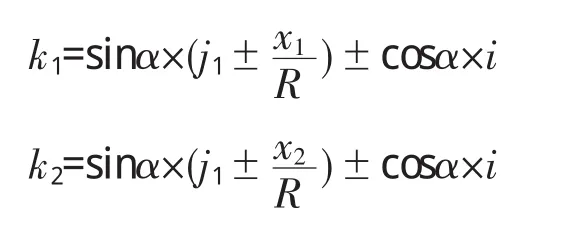
两式相加除2，也即是盖梁中心的实际坡度为

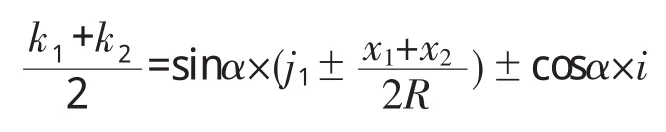
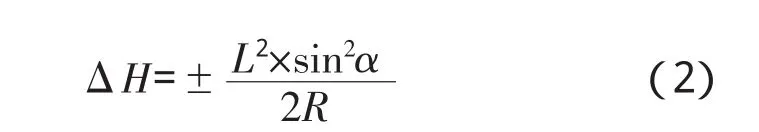
式中：L——盖梁长度；

α——桥梁斜交角；

ΔH——误差；

R——竖曲线半径。

以一个盖梁长20 m，桥梁斜交角为15°，竖曲线半径为2 000 m 为例，以盖梁中心处的实际坡度来模拟整片盖梁的误差不到±7 mm，误差在厘米级以下。

因此，遇到盖梁在桥梁中心线上的投影在竖曲线范围内的情况，计算盖梁的实际坡度时，可以先根据式（2）计算出误差，若误差相较桥面铺装厚度很小甚至可以忽略不计，完全可以用盖梁中心线的实际坡度作为整片盖梁的实际坡度，具体施工时用桥面铺装来调整盖梁形成的误差。

2 结语

在求斜交桥的盖梁坡度时，先确定盖梁两端在道路中心线的投影范围，若该范围的纵坡为一个定值，则该片盖梁的实际坡度也是一个定值，可以直接通过公式k=sinα×j ±cosα×i 来计算，并根据计算出的盖梁实际坡度推出各柱（桩）的顶标高。若该范围在竖曲线内，纵坡不是一个定值，则先根据公式来计算误差，若误差相较桥面铺装厚度很小甚至可以忽略不计，则先确定盖梁中心对应道路中心桩号，求出该中心桩号的纵坡jm，也就是该中心桩号在纵断面竖曲线上的切线的竖直角的正切值（注意纵断面的比例）。将纵坡jm代入k=sinα×jm±cosα×i 求出整片盖梁的实际坡度，并根据盖梁中心对应道路中心桩号的桥面标高推算盖梁中心高程，最后按盖梁的实际坡度推算各柱（桩）顶标高。

[1] CJJ 37-2012,城市道路工程设计规范[S].

[2] JTG D60-2004,公路桥涵通用规范[S].

[3] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[4] 同济大学数学系.高等数学（上册）[M].北京:高等教育出版社,2007.