不同计算方法对边坡稳定性计算影响的实例分析与研究

鲁敏亮，方 振

（珠海市规划设计研究院佛山分院，广东佛山 528300）

0 前言

随着社会经济的发展，边坡稳定性问题越发突出起来，如何定量分析计算边坡稳定安全系数是边坡加固防护研究的关键问题[1]。它在为边坡稳定性进行评价的同时,也为工程技术人员合理设计工程及整治边坡提供主要的设计依据。

1 几种计算方法

当前,边坡稳定性分析计算方法发展迅速,研究方法丰富多样，但是每种方法都有各自的优点和缺点。

1.1 数值分析法

数值分析法在处理非线性、复杂边界、非均质、边坡稳定性的分析的领域中比较实用[2]。它能够给出岩土体应力-应变的关系,在分析坡岩土体与加固结构的相互作用、边坡工程中分步开挖、地下水渗流、爆破等因素对边坡稳定性影响分析方面比极限平衡法更加精确和可靠。主要的计算方法有:边界元法、有限元法、快速拉格朗日法、不连续变形分析法、流形元法等。

边界元法仅在边界上对潜在滑坡体进行单元划分,适用于小变形均质连续介质。这种方法在无限域或半无限域问题处理更具优势。

有限元法是当前研究最成熟的数值分析法[3]，这种方法一般先确定各离散单元块的应力数值,确定滑坡滑动范围和坐标,然后将单元块的破坏与滑坡体的整体破坏结合起来综合分析,不足之处是要求勘察过程中的实测值必须准确无误，因此在应力集中等问题的领域中应用不是很适合。

快速拉格朗日法主要是综合流体中所有质点流体中各点的速度、位移、加速度等参数随时间变化的规律,进而得到研究质点的规律[4]。其不足之处是边界和网格的离散性较大，数据难以收敛。

不连续变形分析法克服了岩体的大变形和大位移的问题,这种方法适合极限状态的设计计算，通过求解平衡方程,按最小势能的原理对势能泛函取最小值得到安全系数。

1.2 极限平衡法

极限平衡法是岩土体稳定计算性分析的主要方法。稳定性系数等于岩石或者土体中潜在破坏面上单元块沿破坏面的抗剪力与该单元块体沿破坏面的剪切力之比[5～7]。通常假定一破坏面来分析岩体和土体的稳定性,取破坏面内的单元体,计算出作用于滑动体上的作用合力达到静力平衡时所需要的抗力或者抗剪强度数值,并与破坏面实际所能提供的抗力或者抗剪强度相比值,从而求得边坡的滑动安全系数。目前极限平衡法的主要的计算方法包括:瑞典圆弧条分法、简布法、简化毕肖普法、萨尔玛法等。

圆弧法在岩石边坡稳定性的分析中比较精确，这是由于岩石边坡破坏面一般是非圆弧形的滑动面，所以只有在均质各向同性的岩体及破碎或松散岩体中计算结果才能接近于实际。。

简布法把滑坡体水平力和竖向力平衡考虑进来,对任意形状滑裂面的边坡稳定计算更加接近实际,但计算安全系数的过程非常繁琐和复杂并且简布法很难满足力矩平衡,需要反复迭代，并且容易产生误差。因而在实际工程中采用这种方法不是很常见。

毕肖普条分法[8]将圆弧滑动体分为若干等宽垂直的条块，分别求其自重并且将重力分解成与滑动面相切和正交的两个分力，通过圆弧的圆心为力矩中心建立力矩平衡方程，求解方程算得滑动安全稳定系数。条分法假设条块间的作用力为水平力,不考虑条块间竖向剪力差的影响,简化了计算,同时精度也没有降低。所以在实际工程中被广泛的应用。

萨尔玛法是极限平衡法的更进一步发展。这种方法在我国广泛用于露天矿边坡稳定性计算分析中。该法更加接近于岩土的受力情况，其缺点是求解过于冗长和繁琐，必须依靠计算机才能更加精确地得出安全系数。

1.3 其他分析方法

其他定性的分析方法包括图解法，工程类比法等，其中图解法主要包括赤平极射投影法和偌谟图法。赤平极射投影法主要是通过作赤平极射投影图，通过投影图更加直接地反应出边坡破坏的边界和各组结构面空间组合的关系,进而判断边坡规模形态，以及可能滑动移动的方向。偌谟图法是用关系曲线和偌谟图表征边坡相关参数之间的定量关系。在中小型工程中这种方法经济实用，而且易于掌握,但是在复杂大型工程的使用中还存在不足,不能精确地判断复杂地质条件下的边坡稳定。

本文主要从工程实例出发，以工程计算软件为工具对常用的几种边坡稳定性计算法进行对比计算分析，研究其适用条件、计算精度,最后通过算例加以验证.从而总结出更适用于实际工程的边坡稳定性分析的方法，以指导工程设计与施工。

2 计算实例与分析

2.1 直线滑动法（见图1）

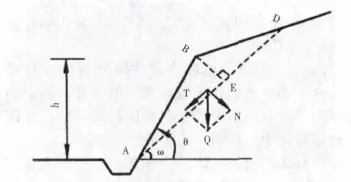
图1 直线滑动面法图示

沿土坡长度方向截取单位长度的土坡,作为平面应变问题来分析.其稳定安全系数为:

安全系数K=抗滑力/下滑力,即：

2.1.1 实例计算

广州萝岗区凤凰五路东延线K0+600～K0+800段左侧边坡（见图2、图3）。

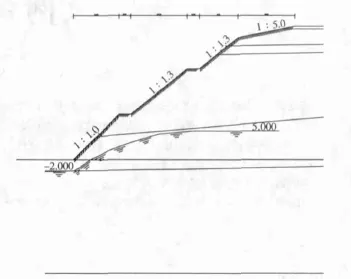
图2 边坡分段计算简图（一）

图3 边坡滑动面示意图（一）

2.1.2 控制参数

地震烈度:7度；水平地震系数:0.100；地震作用综合系数:0.250；地震作用重要性系数:1.000。

地震力作用位置:质心处水平加速度分布类型：矩形。

表1、表2为土层信息表。

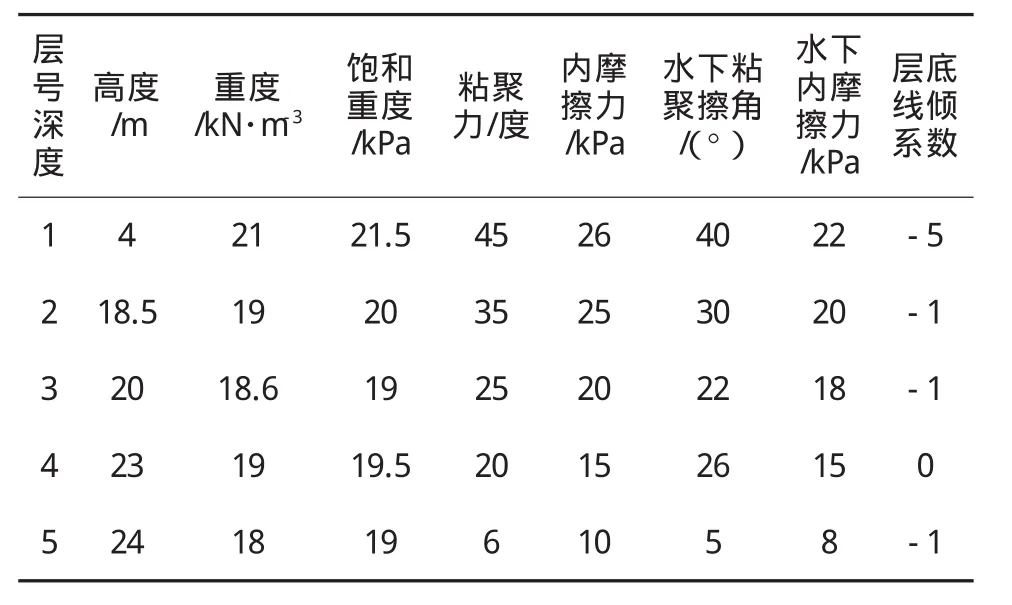
表1 土层信息表

表2 下部土层信息表

2.1.3 计算结果（见表3）

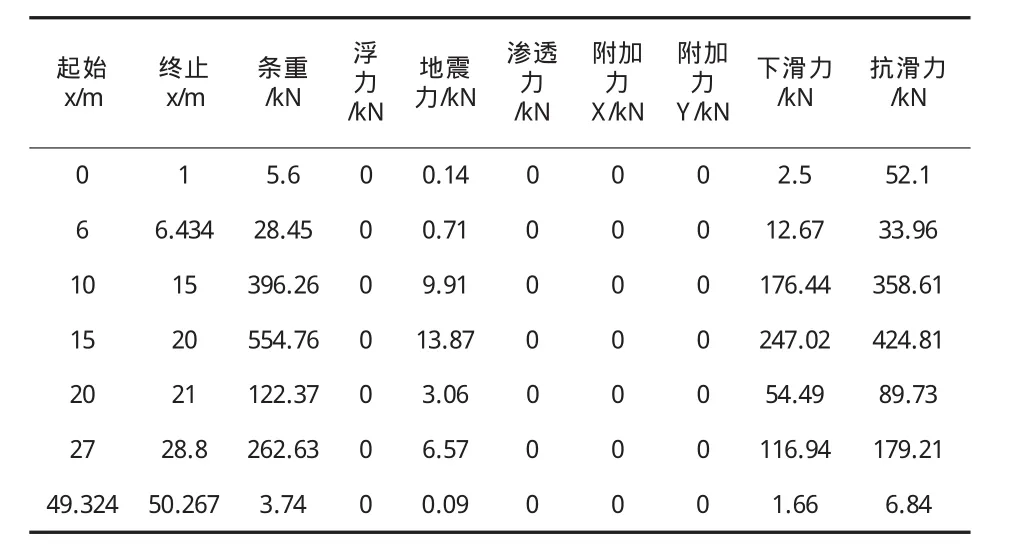
表3 分段计算数据表（一）

总的下滑力=1 959.986(kN)；

总的抗滑力=3 674.702(kN)；

土体部分下滑力 =1 959.986(kN)；

土体部分抗滑力 =3 674.702(kN)；

破裂面仰角:25.000(°)；

安全系数 =1.875。

2.2 瑞典条分法（见图4）

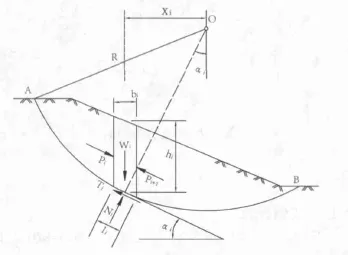
图4 瑞典条分法图示

2.2.1 实例计算

广州萝岗区凤凰五路东延线K0+600～K0+800段左侧边坡（见图5、图6）。

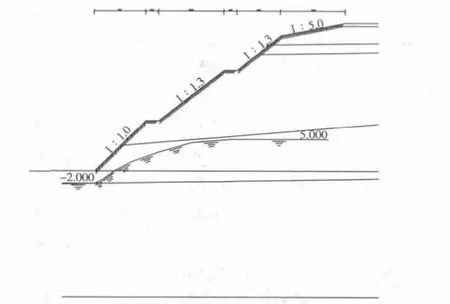
图5 边坡分段计算简图（二）

图6 边坡滑动面示意图（二）

2.2.2 控制参数

地震烈度:7度；水平地震系数:0.100；地震作用综合系数:0.250；地震作用重要性系数:1.000。

地震力作用位置:质心处水平加速度分布类型：矩形。

2.2.3 计算结果（见表4）

总的下滑力 =3 585.889(kN)；

总的抗滑力=4 601.951(kN)；

土体部分下滑力=3 585.889(kN)；

土体部分抗滑力=4 601.951(kN)；

滑动圆心=(4.434,32.816)(m)；

滑动半径=34.717(m)；

滑动安全系数=1.283。

2.3 简化Bishop法（见图7）

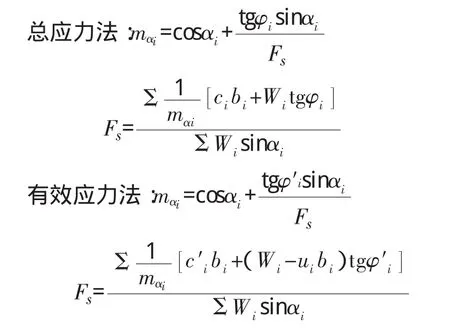
表4 分段计算数据表（二）

图7 简化Bishop法图示

2.3.1 实例计算

广州萝岗区凤凰五路东延线K0+600～K0+800段左侧边坡(见图8、图9)。

图8 边坡分段计算简图（三）

图9 边坡滑动面示意图（三）

2.3.2 控制参数

地震烈度:7度；水平地震系数:0.100；地震作用综合系数:0.250；地震作用重要性系数:1.000。

地震力作用位置:质心处水平加速度分布类型：矩形。

2.3.3 计算结果（见表5）

总的下滑力=3 287.537(kN)；

总的抗滑力=4 440.778(kN)；

土体部分下滑力=3 287.537(kN)；

土体部分抗滑力 =4 440.778(kN)；

滑动圆心=(2.217,37.504)(m)；

滑动半径=38.771(m)；

滑动安全系数=1.351。

2.4 简化Janbu法（见图10）

2.4.1 实例计算

广州萝岗区凤凰五路东延线K0+600～K0+800段左侧边坡（见图11、图12）。

2.4.2 控制参数

地震烈度:7度；水平地震系数:0.100；地震作用综合系数:0.250；地震作用重要性系数:1.000。

地震力作用位置:质心处水平加速度分布类型：矩形。

2.4.3 计算结果(见表6)

总的下滑力=3 320.517(kN)；

总的抗滑力=4 505.101(kN)；

土体部分下滑力=3 320.517(kN)；

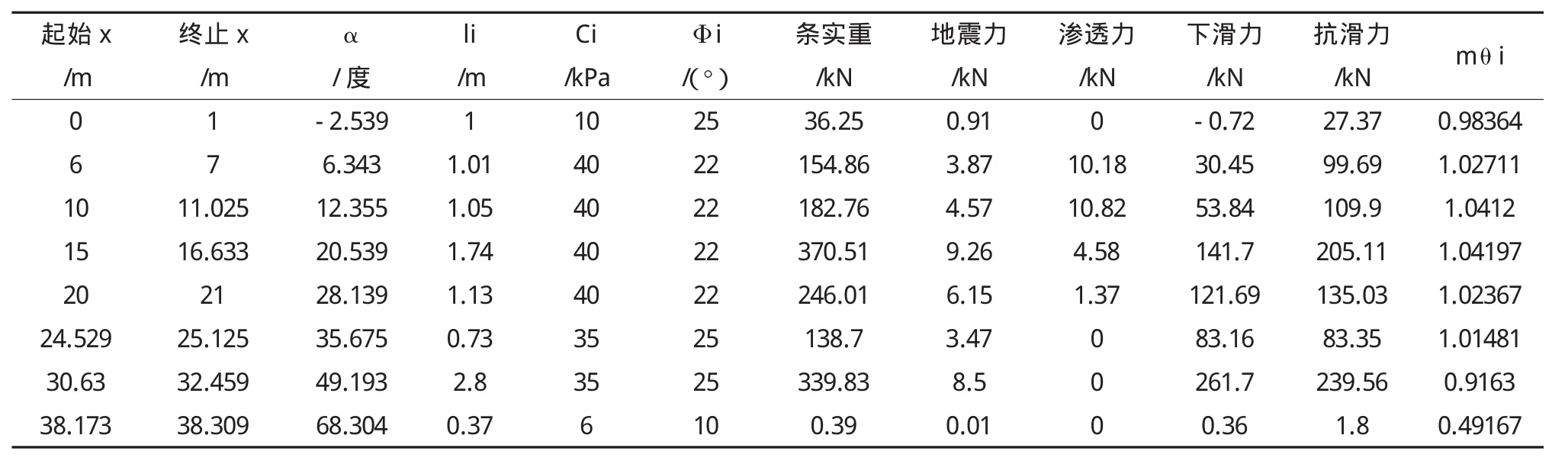
表5 分段计算数据表（三）

表6 分段计算数据表（四）

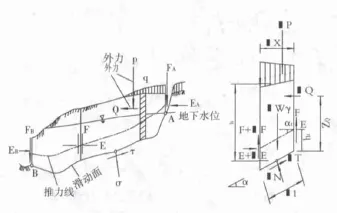
图10 简化Janbu法图示

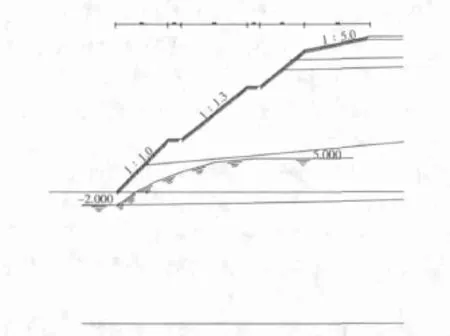
图11 边坡分段计算简图（四）

图12 边坡滑动面示意图（四）

土体部分抗滑力=4 505.101(kN)；

滑动圆心=(2.217,39.848)(m)；

滑动半径=40.814(m)；

滑动安全系数=1.357。

3 结论

上述四种计算方法的滑动安全系数汇总如表7所列。

表7 安全系数对比分析表

通过上述4个算例结果的比较,可以得到以下结论:

（1）直线滑动面法计算的结果偏大，与实际误差较大，该方法适用于破裂面比较平直的均质边坡,如果将其运用于计算土质边坡则计算的稳定系数会与实际情况相差较大。

（2）瑞典条分法由于不考虑土条两侧作用力,算例地段的地区土质以砂质粘性土为主，遇水易软化、泥化，土块间相互作用很明显，计算结果偏于安全.因此安全系数是4种方法中最小的。

（3）简化的毕肖普法和简化Janbu法考虑了条间推力，受力更加合理，其安全系数比直线滑动法和瑞典条分法都大，综合4种方法，简化的毕肖普法和简化Janbu法计算结果最为接近，也更加贴实际。

综合以上分析，由于路堑是从天然土层或岩层中开挖而成的,边坡土体的力学性质离散性比较大,在选用边坡稳定计算方法的时候一定要具体问题具体分析，结合实际情况选用恰当的计算方法，否则就不能在工程设计与施工中提供可靠和确切的计算依据。

[1]黄昌乾,丁恩保.边坡工程常用稳定分析方法[J].水电站设计,1999,15(1):53-54.

[2]钱志雄.岩质边坡破坏模式与结构面关系[J].重庆建筑，2001,（5）:2-4.

[3]周文辅.岩质边坡稳定性的试验研究与计算方法[M].北京:科学出版社,1981:87-140.

[4]郑颖人.岩石边坡支挡结构上岩石压力计算方法探讨.岩石力学与工程[J],1997,16(6):529-535.

[5]王勤成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,2002：38-258.

[6]刘小丽,周德培.岩土边坡系统稳定性评价初探[J].岩石力学与工程学报.2002,21(9):1378-1382.

[7]交通部第二公路勘察设计院.公路设计手册(路基)[M].北京:人民交通出版,1996:48-50.