不同车速条件下路表弯沉的变化规律
2014-01-08代茂华梁毅超练象平
代茂华,梁毅超,练象平
(天津市市政工程设计研究院,天津市 300051)
0 前言
汽车行驶在路面上,由于路表的不平整性,会产生附加的竖向加速度,导致路表弯沉高于静载下的弯沉值。随着车辆行驶速度提高,上述动力效应将更加显著。以静态计算手段为基础的现有设计方法,低估了路表弯沉的实际水平,不利于正确认识车辆荷载作用下公路的耐久性。
众多学者计算分析了车辆荷载作用下的路表弯沉:罗辉、朱宏平[1]对多层沥青路面在移动荷载作用下的动态响应进行了分析,认为提高行车速度可以延长路面的使用寿命;郝大力、王秉纲[2]对车轮荷载作用下的层状体系路面结构响应分析后,指出车速越高,荷载作用时间越短,路表弯沉越小;陈华[3]通过对路基路面动力响应进行非线性数值分析,确定上路堤是控制路基路面永久变形的薄弱位置;梁毅超[4]定量分析了高速重载对路基路面的影响,明确高车速导致路面疲劳寿命下降。
上述研究结论表明,采用动态方法计算路表弯沉更加符合实际情况,然而,之前众多的动力分析中,普遍采用了静态材料参数,同时没有考虑车轮对路面的冲击作用,难以保证计算结果的准确性。据此,本文依托海南省一级公路项目,采用大型通用有限元软件ABAQUS,建立公路三维有限元模型,利用FORTRAN语言编写动态车辆荷载模型,选用动态材料参数,计算得到多种车速条件下路表弯沉的动态响应值,采用对比分析手段,基本掌握了路表弯沉与车速间的关系,研究成果对包括依托工程在内的公路设计具有指导意义。
1 有限元模型
为计算不同车速下的路表弯沉,进而掌握车速与路表弯沉间的关系,本研究需建立公路路基路面模型、车辆荷载模型、材料本构模型。
1.1 路基路面模型
按照依托工程设计方案中的实际尺寸,建立了单车道公路模型,路面组合与厚度如表1所示。参考已有研究中的模型[1-5],确定了公路有限元模型尺寸,如表2所示。根据路面路基的实际受力状态,设置了模型边界条件,如表2所示。

表1 路基路面结构与材料参数

表2 模型尺寸与边界条件
1.2 车辆荷载模型
轮胎与路面间的接触压力采用均布作用形式,轮胎充气压力为0.7 MPa,与标准荷载BZZ-100保持一致。在有限元软件中,标准荷载的圆形轮印建模困难。为解决这一问题,本文中统一将轮印转换为矩形,矩形面积与标准轴载的轮印面积相等,可在最大程度上确保准确性[5],转换公式见式(1)。

式(1)中:A为荷载作用面积;R为标准轴载圆半径;0.4L、0.6L分别为矩形轮印的短、长边。
依托工程设计速度为60 km/h,部分路段车辆实际行驶速度可能提高或降低,故车辆模型的行驶速度分别取 40 km/h、60 km/h、80 km/h、100 km/h。由于路面的不平整性,车轮与路面存在冲击,两者间接触压力超过轮胎的充气压力,通常以动载系数(DLC)表征,定义见式2,该系数取值与速度相关。

式(2)中:σp为车辆动态轮胎力标准差;P为静态轮胎力。
参照文献[4]后,确定了路面平整度为良好时,不同车速下的动载系数,取值见表3。

表3 不同车速时的动载系数
利用ABAQUS的用户子程序接口,以Fortran语言编写了车辆动载模型子程序,模型运行效果与真实车辆行驶状态相同,并可灵活控制车速、轴重、车辆轴型等要素,为本研究带来了极大的便利。车辆动载模型用户子程序界面如图1所示。

图1 车辆动载模型用户子程序
1.3 材料本构模型
模型采用线弹性本构,计算路表弯沉需确定材料的密度、回弹模量、泊松比及阻尼参数;做动力分析,应选用动态回弹模量。王旭东[6]研究认为,对于路面材料,其动模量大约为静模量的2~3倍。徐祝杰[7]对金山大道半刚性基层、土基模量研究显示,半刚性基层动静模量比为3∶1,动模量介于2 200~4 500 MPa。针对不同材料,本文中采用的动态模量见表1。
动力分析时,需确定瑞利利兹阻尼系数α|β:

式(3)中:ω1为结构的基本固有频率;λ1为该频率时的阻尼比。散体材料ω1为8.2,路面材料ω1为18.6,材料阻尼比 λ1皆取为 5%[8]。
2 路表弯沉计算
分别计算了不考虑动载系数和考虑动载系数条件下,车速在40~100 km/h变化时的路表弯沉。不考虑动载系数时,路表弯沉计算结果见图2。单根曲线来看,路表弯沉变化分为两个阶段:(1)随着时间后移,路表弯沉逐渐增大,直至峰值弯沉;(2)随后曲线迅速下降,路面变形由压转拉,并逐渐回升至x轴附近,路表弯沉归零,车辆荷载对路面已无影响。
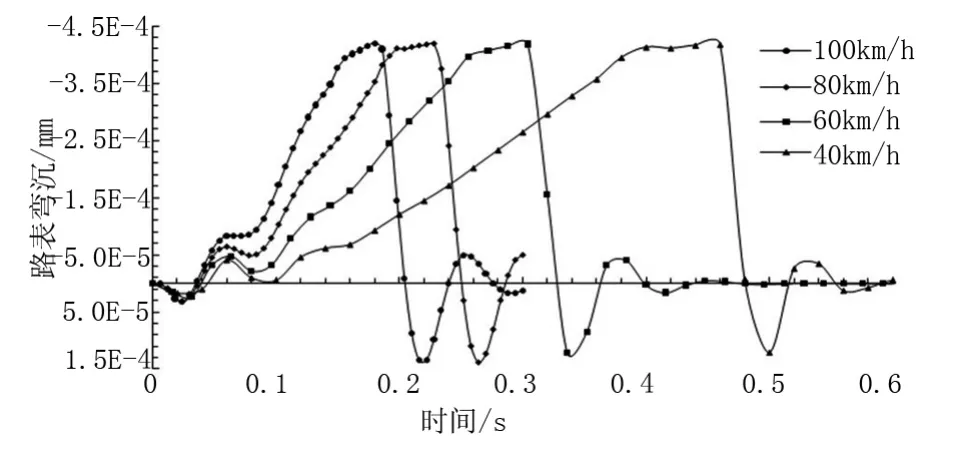
图2 无动载系数时,不同车速下路表弯沉时变曲线
不同车速下,路表弯沉时变曲线对比显示,阶段1的曲线受车速影响较大,随着车辆速度的增加,阶段1曲线斜率迅速增加;但车速对路表弯沉峰值影响轻微,车速由100 km/h下降至40 km/h,路表弯沉峰值仅下降0.5%左右。阶段2曲线的趋势基本不受车速变化的影响,路面拉变峰值则出现了较为明显的下降,同样车速由100 km/h下降到40 km/h,拉变峰值下降了9.5%。无动载系数时,不同车速的车辆动载作用于路面,路表在阶段1产生压缩变形,阶段2产生一定的拉伸变形,两变形的差值随车速增加而显著增大,显示路面承载部位的交变应力幅度将随着车速增加而增大,加快了路面疲劳破坏的速度,这一特点静态计算无法体现,可能低估车辆荷载对路面的影响。
考虑动载系数时,路表弯沉计算结果见图3。无论是阶段1还是阶段2,单根曲线的趋势与之前无动载系数时的曲线一致,因此多根曲线间对比与前述规律相同。考虑了动载系数后,不同车速下路表弯沉的峰值有一定的差异。阶段1曲线显示,车速由100 km/h变为40 km/h,路表弯沉峰值下降了5%;平均来看,车速每下降20 km/h,路表弯沉峰值随之下降1.5%左右。阶段2内,车速由100 km/h变为40 km/h,路面拉变峰值下降了13.6%。与无动载系数结果相比,有动载系数时阶段1路表弯沉峰值受车速影响较为显著,表明高车速时路表弯沉增量,是车轮与路面间的冲击作用引起的。阶段2的拉伸变形峰值与车速间的规律与阶段1类似,因此高车速动载作用下交变应力幅度大于不考虑动载系数的结果,路面疲劳寿命进一步降低。

图3 有动载系数时,不同车速下路表弯沉时变曲线
图4中分别绘制了无动载系数与有动载系数下,车速40~100 km/h时的路表弯沉峰值曲线。无动载系数时,曲线呈平直线形式,路表弯沉峰值基本不随车速变化而改变;有动载系数时,曲线呈现出明显的上升趋势,直观地体现了车速对路表弯沉的影响,揭示了高车速路表弯沉增加的原因为车轮与路面间的冲击。
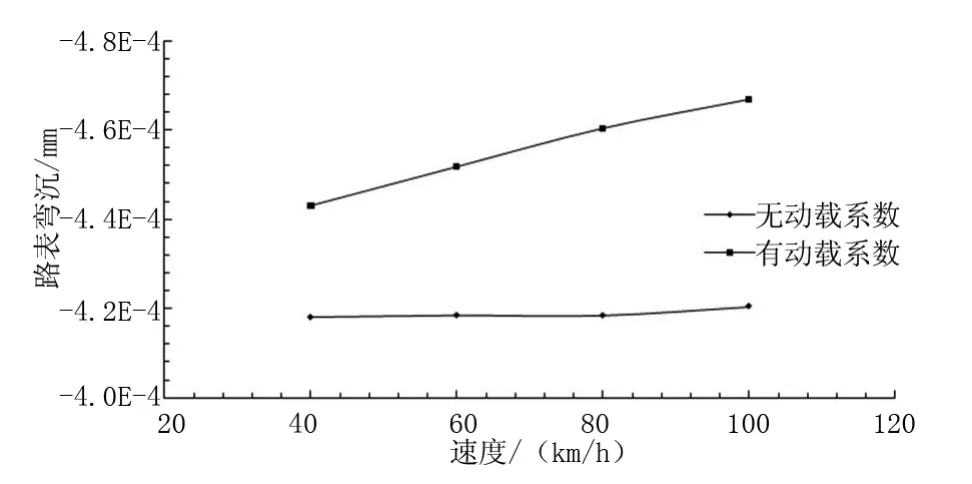
图4 路表弯沉峰值与车速的关系曲线
3 结论
分别计算了无动载系数与有动载系数条件下,多车速车辆动载作用时的路表弯沉,对计算结果分析后,基本掌握了车速变化与路表弯沉间的规律,获得创新性成果与结论如下:
(1)利用ABAQUS用户子程序接口,对车辆荷载进行了二次开发,建立的动载模型符合车辆实际行驶状态,能够对车辆的速度、轴重、轴数、轴距等参数灵活控制。
(2)动载作用下,路表弯沉时变曲线可分为两个阶段:阶段1曲线平缓上升,最终升至路表弯沉的峰值;阶段2曲线迅速下降,路面变形由拉转压,拉伸达到最大后,变形逐步恢复至未加载状态。
(3)不考虑动载系数时,车速由40 km/h提高至100 km/h,路表弯沉峰值仅上升0.5%;考虑动载系数时,车速发生同样的变化,路表弯沉峰值上升了5%;车速每上升20 km/h,峰值平均上升1.5%,表明高车速路表弯沉的增量,是轮胎与路面间冲击作用引起的。
(4)相比静力计算,动力计算结果显示高车速条件下,路面疲劳寿命将出现下降。
[1]罗辉,朱宏平,郝行舟.沥青路面动态响应数值分析[J].交通运输工程学报,2007,8(7):44-47.
[2]郝大力,王秉纲.路面结构动力响应分析[J].长安大学学报(自然科学版),2002,5(22):9-11.
[3]陈华.交通荷载作用下公路路基的动力有限元分析 [D].兰州:兰州理工大学,2004.
[4]梁毅超.高速重载条件下路基路面的动态力学响应 [D].上海:同济大学,2013.
[5]周亮.考虑环境因素的沥青路面疲劳性能预估模型 [D].上海:同济大学,2011.
[6]王旭东.沥青路面材料动力特性与动态参数[M].北京:人民交通出版社,2008.
[7]徐祝杰,凌建明,黄琴龙.旧水泥混凝土共振碎石化路面模量分析[J].同济大学学报(自然科学版):2008,36(9):1195-1209.
[8]黄琴龙,凌建明.路基工作区的确定方法研究[J].同济大学学报(自然科学版),2011,39(4):551-555.
