坡面雨水汇流状态分析及雨水量计算

元绍建，陈娅倩

(1.天津市市政工程设计研究院，天津市 300051；2.天津市自来水集团津南水务有限公司，天津市 300000)

0 引 言

初始降落到路面的雨滴，受到横坡和纵坡下滑力的合力作用而沿道路斜面做直线运动，当雨水汇流到侧石处时，将形成沿着侧石方向的类似于明渠水流的流态，该流体沿程不断接收路面雨水，流量不断变大直至汇入坡与水平道路衔接处附近的收水井内为止。整个过程主要包括两种流态：（1）雨水路面流动状态；（2）雨水沿侧石的类似明渠水流状态。为了准确计算雨水沿坡的水量，需要对这两种水流状态进行简要分析，并合理适当简化。

1 路面雨水水流状态分析

降落在路面上的雨水，首先有部分渗透到路面，然后逐渐形成路面表层水膜并流动，降雨强度的大小只代表同等时间降雨量的多少，同时影响路面形成径流的时间，但这个过程很短暂，当降雨在路面形成径流后，不同降雨强度下对于单个雨滴来说在路面的流动速度相同[1]。

经分析影响雨滴水流状态的参数应是道路的横断面宽度、横坡、纵坡和路面粗糙系数。取单个雨滴作为受力对象进行分析，见图1。

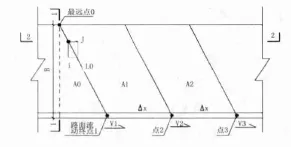
图1 路面雨水汇流分析平面图

对雨滴在纵剖面和横剖面上分别作受力分析，单个雨滴受到的力包括：重力G、摩擦力、支持力和位于周边的其他雨滴单元给予的力，其中其他雨滴对雨滴单元的力可相互抵消，另外三个力的合力使雨滴单元产生沿坡向下的加速度，见图2、图3。横纵两个方向的加速使雨滴单元形成图1所示方向的速度，速度方向与道路边线的夹角与道路横纵坡比值有关。

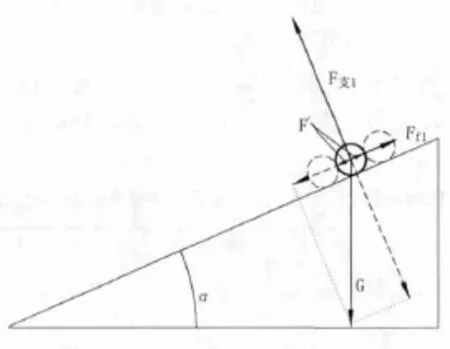
图2 横剖面受力分析

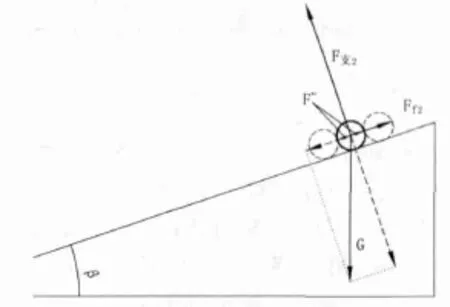
图3 纵剖面受力分析

图中各参数的经验公式有：

式中：i——道路横坡；

J——道路纵坡；

i0——横坡与纵坡的合并坡度；

L0——路面流行长度；

t0——雨水路面汇水时间；

n——粗糙系数。

2 沿侧石方向类似明渠雨水流动状态分析

侧石处得的水流为类似于明渠式的水流，跟普通明渠不同的是，其横断面并非矩形，而是三角形，见图4。沿着纵坡向下该类明渠不断接收路面汇集过来的雨水，使明渠雨水流量不断变大，所以侧石处水位也在不断变大，而流速是流量与明渠横截面积的比值，根据物体沿斜坡向下滑动的普遍规律，雨水流动的速度应不断变大，但基于流体的特殊性，流速变化情况比较复杂，变化情况须通过计算得知。

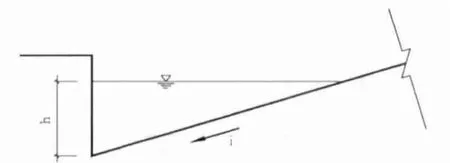
图4 道路侧石处类明渠横断面

根据曼宁公式—明渠道速度经验公式：

式中：k——转换常数，国际单位制中值为1；

n——曼宁系数，反应管渠壁的粗糙系数，这里是路面及侧石的粗糙系数；

R——水力半径，是流体截面积与湿周长的比值。

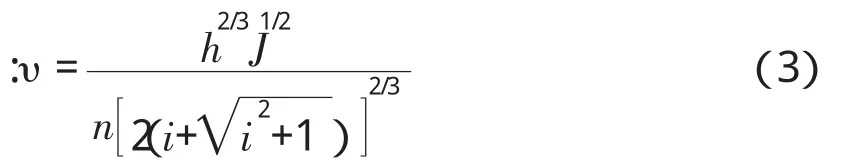
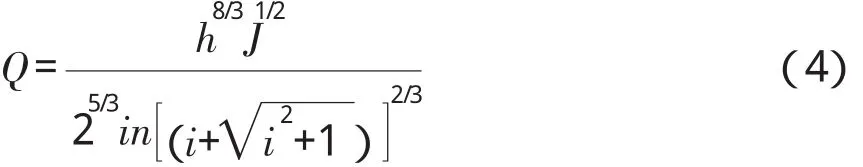
其中n、i、J皆为定值，此式为流量v、Q与水深h的相互关系式。

3 定长度坡面雨水量计算

如图1所示，雨滴由最远点0开始流动，先沿路面汇流至点1。路面汇水时间为t0，根据暴雨强度公式得点1处雨水流量根据式（3）可以计算 h1，在通过式（4）计算横截面平均流速v1，并将v1简化为点1至点2的类明渠平均流速，这样点1～2间的雨水流行时间t1～2＝Δx/ν1，则最远点 0至点 2间汇水时间 t0～2=t0+t1～2，然后流量Q和流速等计算如前所述，迭代计算次数为定长度L/Δx。

这些重复性的计算可以通过编写Excle表格来进行计算。由于将每一段的起点流速简化为本段明渠雨水流动的平均流速，可以发现本段间距Δx越小计算流量将会越精确，Δx→0时流量达到峰值即实际流量。

4 计算举例及关系曲线拟合

通过应用上述公式编写Excle表格来计算宽2B=40 m，横向坡度 i=0.02，纵向坡度 J=0.02，粗糙系数n为0.013的道路坡面上点1下游1 000 m处的实际雨水流量。在不同Δx间距下得点1下游1000m处流量值见表1。

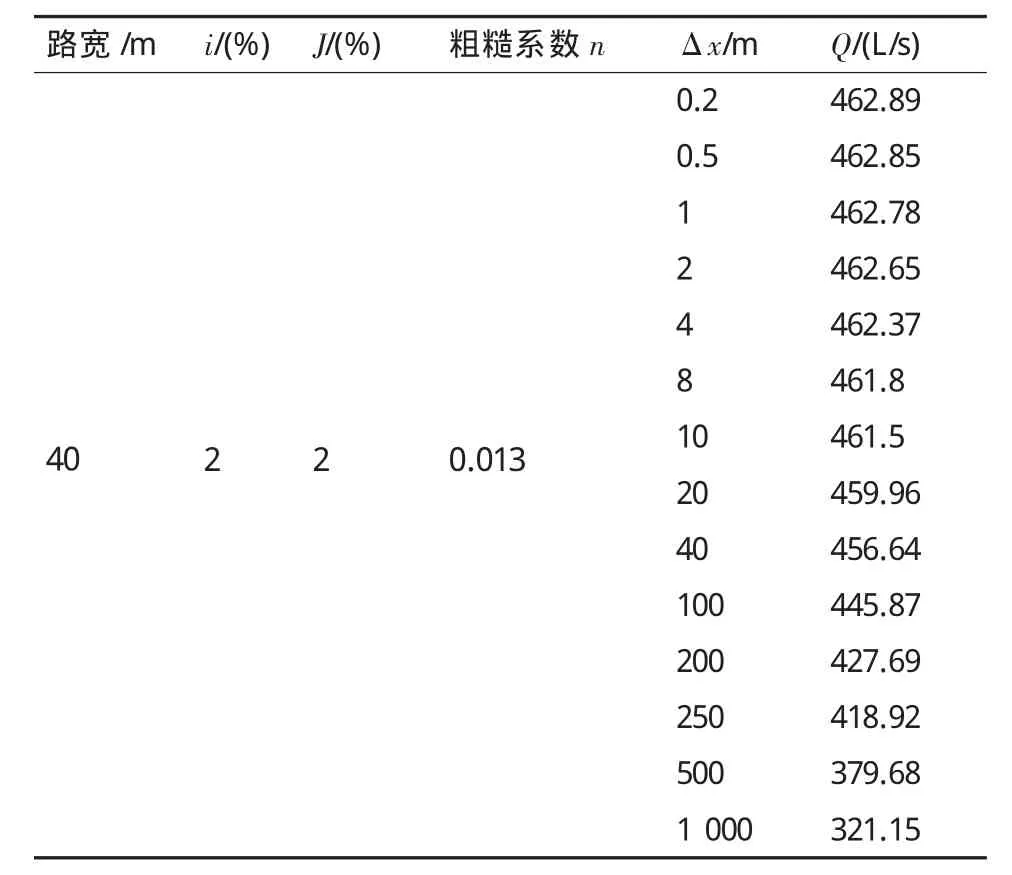
表1 不同Δx间距下点1下游1 000 m处流量值(P=2，Ψ=0.9)

并以Δx=10 m为例计算点1至下游1 000 m内，不同距离处流速，见表2。

表2 Δx=10 m时，点1下游不同距离处的流速

将表1中Δx值对应的Q值绘制成图，并用3次多项式拟合，见图5。

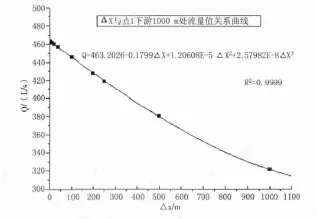
图5 △x与Q关系曲线

将表2绘制成曲线，见图6。

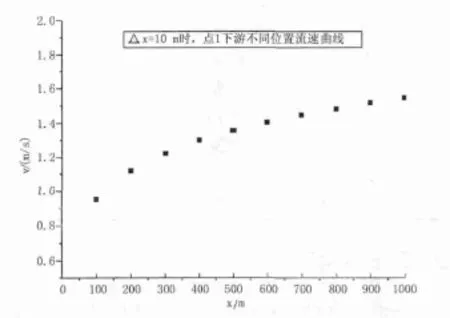
图6 流速v与点1下游不同距离x关系曲线

5 结论

（1）由图5所得三次函数在Δx=0处连续且可导，则Δx→0的极限值Qmax等于Δx=0时的函数值约为463.20(L/s)，应用同样的方法亦可以求得其他固定长度时的实际坡面流量。

（2）根据图6可知，随雨水向下游流动，类明渠内雨水的横断面平均流速不断变大，其变化符合对数曲线规律。

[1]陈云鹤,等.漫流排水时公路路面及边坡的水流速度计算[J].公路交通科技,2003(10)：20-23.