从力学角度分析各类汞柱流出问题

赖佳颖 张秀梅

（复旦大学附属中学，上海 200433）

各类汞柱流出问题是高中热学部分的难题，它需要学生具有较强的综合分析能力和运用数学知识能力.在不少教辅书中，往往换一道题目，就会换一种解法，且常常突出数学计算而缺少物理意义的解析，令人费解.笔者从力学角度分析汞柱受力平衡条件结合气体状态分析，给出解决汞柱流出问题一种统一解法.

1 玻璃管倒置后汞柱流出问题

例1.一根长为L的均匀直玻璃管，开口向上，管内有一段长为h的汞柱封闭了一段长为l的理想气体，如图1，当玻璃管缓慢转动直至其开口竖直向下，则应分别满足什么条件，水银将不会、部分或者全部流出？（已知水银的密度为ρ，外界大气压强为p0，且p0≥ρgh.）

解析：在玻璃管缓慢转动时，管内部气体等温膨胀，由于玻璃管的长度有限，所以到管口竖直向下时，汞柱可能不会、部分或者全部流出玻璃管，具体分析如下.

图1

图2

假设水银流出了一部分，留在管内的水银柱长为x（如图2），如果此状态水银柱恰好处于平衡状态，则有部分水银可留在管内.设内部气体压强为p3，即p3满足

而气体状态满足

联立（1）、（2）式解得

其中0＜x＜h，p0≥ρgh.

根据（3）式不难看出等号右侧为一个随x减小而单调递增的函数.当x＝h时，函数最小，（p0＋ρgh）l＝（p0－ρgh）（L－h），表示此时水银恰好没有流出；当x＝0时，函数最大，（p0＋ρgh）l＝p0L，表示此时汞柱恰好全部流出，所以满足（p0－ρgh）（L－h）＜（p0＋ρgh）l＜p0L时水银部分流出.

当（p0＋ρgh）l≤（p0－ρgh）（L－h）时，水银不流出；

当（p0－ρgh）（L－h）＜（p0＋ρgh）l＜p0L时，水银部分流出；

当（p0＋ρgh）l≥p0L时，水银全部流出.

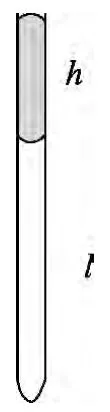
图3

2 滴入及吸出竖直管中水银的问题

例2.竖直放置且开口向上的玻璃管中，有长为h的水银柱封住一段长为l的空气柱，水银柱与玻璃管开口齐平（如图3），已知水银的密度为ρ，外界大气压为p0，下列变化的整个过程，气体温度始终保持不变.试问：

（1）若从管口向该管内滴入水银，则p0、h、l应满足什么条件才能在玻璃管口滴入水银后不溢出？

（2）若从该管内吸出水银，则p0、h、l应满足什么条件才能在玻璃管口吸出部分水银后管内汞柱能全部溢出？

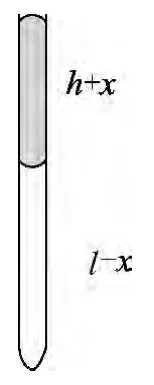
图4

解析：（1）从管口向管内滴入少量水银，设滴入的水银柱长为x（x＞0），若此时水银柱与管口相平，它受到的合力为0或方向竖直向下，这代表汞柱能全部留在管内而不溢出.设此时气体压强为p1，即满足

气体状态，根据气态方程可得

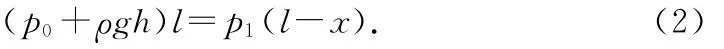
（2）从管内吸出水银，此类问题与（1）相似，设汞柱被吸出长为x后，管内汞柱与玻璃管开口齐平时（如图5），它受到的合力方向竖直向上，则水银将会自动溢出.设此状态气体压强为p2，即满足

气体状态根据气态方程可得

由（3）、（4）式可解得

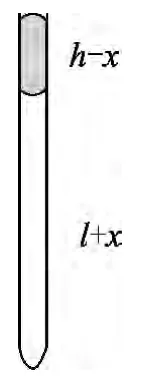
图5

通过以上的分类讨论，我们不难发现，利用气体状态方程结合汞柱平衡条件的判断可以很好地解决各种汞柱流出问题，不仅仅对于本文中所讨论的等温变化，也同样适用于各种升温膨胀问题.这种方法的优点在于统一了不同问题的解题思路，还原了汞柱流出真正的物理特征，即受力不平衡，也让学生可以更好地了解数学不等式所表达的物理意义，方便学生理解和建立解决同类问题的思路，能够做到举一反三.