棉花产量监测系统数据的误差分析与处理研究

陈 伟，马 蓉

（1.中船重工第七一八研究所，河北 邯郸 056027；2.石河子大学机械电气工程学院）

提高农业生产效率的有效方法是根据农田的空间差异性特征建立产量空间分布图，进而对农田实施变量作业管理[1]。作物产量信息是农业生产效率高低最直接而又具体的反映,依据农田作物产量数据来生成产量空间分布图是实施精准农业的基础[2],也是最终制定农田管理和实施变量作业，实现农业生产节本增效、降低污染的基础[3]，所以在实施精准农业变量作业管理措施之前,采集农田作物产量数据,生成高精度的产量空间分布图是非常重要的[4]。由于田间工作环境中的地块不平整、灰尘多等多种复杂性因素的影响，以及操作者操作不规范等使得棉花产量数据中带入误差，而且在采棉机采收棉花的过程中，Insight棉花产量监测系统只能进行标定，而对其他设置不能更改，造成误差带入，从而使得Kriging插值成的棉花产量空间分布图的精度降低，影响到精准农业变量作业管理实施的整体效果[5]。所以在Kriging插值生成棉花产量空间分布图之前必须对产量数据误差分析与处理。

1 产量数据采集与预处理

1.1 产量数据的采集

2009年10月，基于采棉机在试验区地块内进行棉花在线测产试验。本试验使用的Insight棉花产量监测系统集成了DGPS、传感器和微处理器等技术[6]，它主要由Insight产量监视器、行走速度传感器、风机转速传感器、采摘头高度传感器、棉花流量传感器和DGPS等组成。Insight产量监测系统每隔1 s记录一个棉花产量数据点。本试验中Insight棉花产量监测系统安装在美国John Deer 9970采棉机上，为获取精度相对较高的原始产量数据，必须对Insight棉花产量监测系统进行GPS补偿设置、各传感器设置、采摘头高度设置和标定等，而标定在整个棉花测产过程中是最为重要的[7]。标定包括质量标定、行驶距离标定、采摘头停止高度标定和面积标定。各车次棉花产量的测量值与实际值间的相对误差见表1。产量、距离和面积在标定前后的相对误差对比见表2。

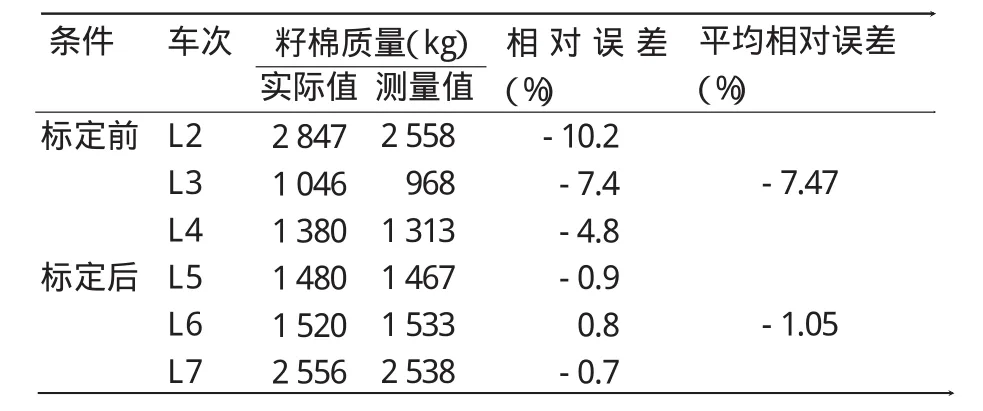
表1 各车次棉花产量的测量值与实际值间的相对误差

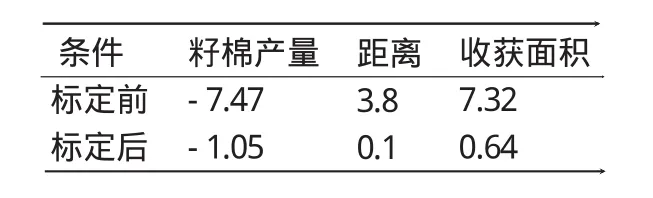
表2 产量、距离和面积在标定前后的相对误差（单位：%）

1.2 产量数据的预处理

Insight棉花产量监测系统采集到的棉花产量实时数据以.YLD格式存储，须使用与Insight棉花产量监测系统相配套的美国凯斯公司的专业软件Advanced Farming Systems来读取数据，但AFS软件并不能进行误差处理。因此首先应用AFS软件将.YLD格式的棉花产量数据文件输出转换成shape格式的文件，进而运用统计学软件ArcGIS对表达棉花产量数据空间位置的大地坐标系转换为二维的可直接进行距离和面积计算的UTM WGS84平面直角坐标系，从而为棉花产量数据的误差处理做好准备。

2 产量数据误差分析

在棉花产量实时自动测产过程中，会受到使用的仪器、设备情况、所处的自然环境条件以及人员操作的规范等多种因素的影响，使测产结果产生误差[8]。根据误差的性质和特点，可将棉花产量数据误差分为系统误差、粗大误差和随机误差[9~10]。

2.1 系统误差

系统误差由按一定周期规律变化的因素造成[11]。消除系统误差最有效的方法是消除产生系统误差的来源。在采棉机收获棉花的过程中，Insight棉花产量监测系统虽然完成了正确的安装和调试，而且经过了多次标定来减少误差的带入，但由于田间地块不平整等相关因素的影响，使得采棉机在作业过程中轮胎经常打滑，从而造成行走速度传感器测得的车速偏高,形成系统误差。为减少系统误差的带入，可以剔除采棉机作业平均速度±2倍标准差范围外的速度数据点。

2.2 粗大误差

产量数据中粗大误差的带入往往源自于人员操作不规范，造成数据出现异常值，而棉花产量数据的采集是实时在线的，无法进行再来一次的测量，所以可以根据棉田管理情况和种植经验等来剔除异常值。在采集的棉花产量数据中有小部分的产量值特别高，也有小部分的产量值特别低，而绝大部分数据点的产量值都在5.2 t/hm2左右。由于整个试验地块区域内采取的管理方式是一样的，所以棉花产量值相差不大。依据种植情况、经验等将棉花产量数据处于1.5~7.4 t/hm2之间的归为正常值，而剔除掉不在此范围内的异常值。

2.3 随机误差

随机误差的产生因素十分复杂，如果棉花产量数据中没有系统误差和粗大误差，则包含有随机误差的数据一般服从正态分布。下图为5号地棉花产量数据的正态QQPlot图，它接近一条直线，表明该数据服从正态分布，也进一步说明剔除掉异常值，有效减少了系统误差和粗大误差。由于随机误差是不能避免产生的，所以采棉机采收棉花的过程中，可适当地增加标定的次数、规范人员操作方法等手段来降低随机误差和系统误差。

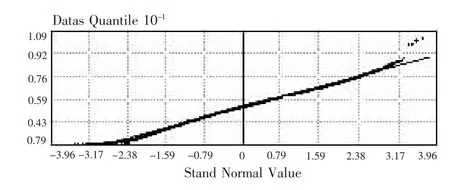
图1 5号地数据的QQPlot图

3 产量数据的处理方法

处理棉花产量数据点的异常值的方法有许多，一是可以直接剔除掉异常值，二是可以用总体数据的平均值来替代异常值，三是可以用正常值中的最大值来代替异常值等[12]。因为Insight棉花产量监测系统每秒钟采集一个数据点，所以数据点很庞大，而剔除掉一些点对整个试验田块内的棉花产量空间分布情况影响不大，所以可以运用直接剔除异常值的方法。

3.1 阈值过滤器设计

运用阈值过滤直接剔除异常点的方法。依据种植情况、经验等将棉花产量数据处于1.5~7.4 t/hm2之间的归为正常值，而剔除掉不在此范围内的异常值。针对采棉机作业过程中轮胎经常打滑的现象，剔除掉不在采棉机作业平均速度±2倍标准差范围内的速度异常数据点。

3.2 结果与分析

表3为试验地内的棉花产量数据误差处理前后的描述性统计结果对比。从表中可以看到，经过误差处理，剔除掉棉花产量数据点异常值后，偏度增大并靠近于零，棉花产量数据趋向于正态分布。经误差处理后,棉花产量数据变异系数CV（%）为19.61%，较处理前的25.18%仅减小了0.0557，这表明，经过误差处理剔除掉数据点异常值后，余下的棉花产量数据不仅保留了原有的产量变异，而且表明试验区地块内的棉花产量数据在空间变异性特征处于中等水平，符合划分精准农业管理分区的条件和指导变量作业的要求。

3.3 误差数据对产量空间分布图的影响

对试验地内的棉花产量数据，在误差处理前后，分别运用地统计学软件ArcGIS，进行Kriging插值。通过对比两棉花产量空间分布图可以看到，经过误差处理后的空间分布图中的异常值数据点大幅度地减少，而且空间分布图的精度、聚类性和平滑性得到了比较明显的提升。

表3 棉花产量的描述性统计分析

4 结语

为了提高经过Kriging插值成的棉花产量空间分布图的精度，必须对棉花产量数据中的误差进行细致而深入的分析，找出产生各种误差的原因，从而采取有效的措施和方法来减少、甚至剔除误差。本研究以采集的棉花产量实时数据为基础，分析了产量数据中包含的系统误差，粗大误差和随机误差，设计的阈值过滤器对棉花产量实时数据进行了误差处理。依据种植情况、经验等将棉花产量数据点处于1.5~7.4 t/hm2之间的视为正常值，而剔除掉不在此范围内的异常值数据点；另一方面针对采棉机作业过程中轮胎经常打滑的现象，剔除掉不在采棉机作业平均速度±2倍标准差范围内的速度异常数据点。结果表明，经过误差处理后的棉花产量数据趋于正态分布，不仅保留了原有实际产量数据的变异性，而且试验区地块内的棉花产量数据的空间变异性特征处于中等水平，符合划分精准农业管理分区的条件和指导变量作业的要求。本研究还比较了误差处理前后建立的棉花产量空间分布图，发现经误差处理后Kriging插值成的棉花产量空间分布图中的异常点显著减少，分布图的精度、聚类性和平滑性得到了显著提升。

[1]王长耀,牛铮,唐华俊等.对地观测技术与精细农业[M].北京:中国科学出版社,2001.

[2]薛正平,邓 华,杨星卫等.基于决策树和图层叠置的精准农业产量图分析方法[J].农业工程学报,2006,22(8):140~144.

[3]Panneton1B,Brouillard1M,PiekurowskiT.Integration of yield data from several years into1a1single1map[R].Montpellier,France:Proceedingof the 3rd European Conference on Precision Agriculture,2001.

[4]Missotten B,Strubble G,Baerdemaeker J.Accuracy of grain and straw yield mapping[R].Minnesota:Proceeding of the 3rd international conference on precision agriculture,1996.

[5]Lark R M,Stafford J V.Consistency and change in spatial variability of crop yield over successive seasons,methods of data analysis.In Robert P C,Rust R H,Larson WE(eds)3rd international conference on precision agriculture.ASA,CSS A,SSSA&ASAE,Madison,Wisconsin,USA.1996,141~150.

[6]陈伟，马蓉，卢帅等.机采棉在线测产技术及其关键装备[J].农机化研究，2011,10：216~219.

[7]陈伟,马蓉,卢帅等.Insight棉花产量监测系统及应用研究[J].安徽农业科学，2010,38（30）：17208~17210.

[8]http://baike.baidu.com/view/40051.htm.

[9]梁晋文，陈林才，何贡.误差理论与数据处理[M].中国计盈出版社,2006.

[10]贾沛璋.误差分析与数据处理[M].北京：国防工业出版社,2002.

[11]费业泰.误差理论与数据处理[M].北京：机械工业出版社，1995.

[12]施斌,王宝军,周国云.环境地质学中的GIS[M].北京：科学出版社，2006.