偏微分方程的应用

范俊杰

（武汉理工大学数学系，湖北 武汉 430070）

在科学技术日新月异的发展过程中，人们研究的许多问题用一个自变量的函数来描述已经不够精确了，所以不少问题必须用多个变量的函数来描述，才能够更精确地得到人们所需要的结果。这样就产生了研究某些物理现象的理想的含有多个变量的函数及其偏导数的方程，这种方程就是偏微分方程。实际上，偏微分方程的解一般有无穷多个，而在解决具体物理问题时，我们必须从众多一般解中找到能够满足题目给定的特殊条件的解，这样我们才能够了解具体问题的特殊性。本文在简要的介绍偏微分方程的发展历史的基础上，详细的讨论了其在弦振动及人口问题中的应用。

1 偏微分方程的发展

1746年，达朗贝尔在他的论文《张紧的弦振动时形成的曲线的研究》中，提议证明无穷多种和正弦曲线不同的曲线是振动的模式。由此开创了偏微分方程这门学科。和欧拉同时代的瑞士数学家丹尼尔·贝努利也研究了数学物理方面的问题，提出了解弹性系振动问题的一般方法，对偏微分方程的发展起了比较大的影响。偏微分方程得到迅速发展是在十九世纪，那时候，数学物理问题的研究繁荣起来了，许多数学家都对数学物理问题的解决做出了贡献。这里应该提一提法国数学家傅立叶，他在从事热流动的研究中，写出了《热的解析理论》，在文章中他提出了三维空间的热方程，也就是一种偏微分方程。他的研究对偏微分方程的发展的影响是很大的[3]。

2 偏微分方程在某些具体问题中的应用

2.1 偏微分方程在弦振动中的应用

弦是一个力学系统，是一个质点组，故它的运动符合牛顿第二定律。设弦在未受扰动时平衡位置是x轴，其上各点均以该点的横坐标表示。弦上各点的位移假设发生在某个平面内垂直于x轴的方向上，t时刻的形状是曲线u＝u(x，t)，适当假设如下：

（Ⅰ）弦是一个“柔软”的连续体，之所以能维持其形状是由于弦能抵抗弯矩，因此任何时刻弦的张力总是沿着弦的切线方向，且弦的重力可忽略不计[4]。

（Ⅱ）弦的振动发生在一个平面内，且弦上各点的运动方向垂直于平衡位置。

（Ⅲ）微小是指弦振动的幅度及弦上任意点切线的倾角都很小，u（x，t）是弦上横坐标为x的点在时刻t的位置。

（Ⅳ）弦的扰动是小扰动，即弦上各点的位移与弦长相比很小，且振动平稳即弦在任意位置的倾角都很小，这并不是说u(x，t)的数值很小，而是ux很小。

为了导出弦的横振动方程，我们选择平面直角坐标系，弦的平衡位置为x轴，其两端分别固定在x＝0及x＝1处。

先证明弦上每点张力为常数。在弦上任取M1M2为一小段，M1M2的长度则为，由于假定弦只做微小振动，即可以认为这段在振动过程中并未伸长，由胡克定律可知，弦上每一点所受张力在运动过程中保持不变，即张力与时间t无关。

再证明弦上每点张力也不随地点的变化而变化。将点M1和M2的张力分别记为T1和T2，张力的方向分别沿着弦在点M1和M2处的切方向。由于假定弦只做横向振动，因此张力在x轴方向分量的代数和为零，即有

T2cosβ-T1cosα＝0（α，β 分别是曲线 u（x，t）的切线与 x 轴的夹角）

对于微小振动 α≈0，β≈0，所以 cosα＝cosβ，于是可得 T1＝T2，这说明张力不随地点变化。

综上所述张力为常数，记为T。根据牛顿第二定律可以建立弦的横向振动方向。

作用在弦的这一微小元素上的垂直方向的力即为在横向分量的代数和为：

由于微小振动，所以α，β都较小，即：

应用微分中值定理可将上式化为：

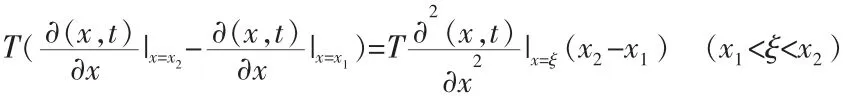
设弦的密度为ρ，由于弦段(x1，x2)较小，所以其上的每点加速度相同，因此可以用其上的任意一点的加速度代替。于是该弦段的惯性力的大小为：

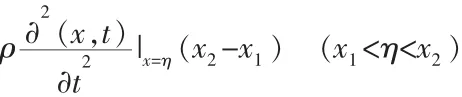
（1）弦自由振动的方程

当弦自由振动时，不受外力，由牛顿第二定律可知合力为惯性力，可得下式：

（2）弦强迫振动方程

若在弦的每单位长度上还有横向外力作用，外力密度为F(x，t)，由于弦段M1和M2很小，其上各点处的外力密度近似相等，故作用在弦段上的外力近似等于[1]：

当x1→x2时，对上式取极限可得：

2.2 偏微分方程在“人口”问题中的应用

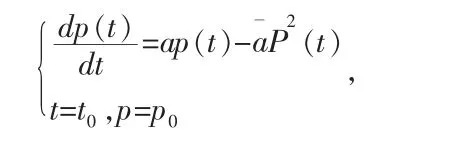
人口问题是生物学家非常感兴趣的问题之一（人口并不仅限于人，它可以是任何一个与人有类似性质的生命群体）。对人口的发展进行研究我们所采用威尔霍斯特模型：其中，a¯称为生命系数，并且a¯比 ɑ 要小很多。 a¯P2（t）就是考虑到生存竞争而引入的竞争项。当群体总数p（t）不太大时，由于a¯比ɑ小很多，则可以略去上面方程中右端的第二项而回到马尔萨斯模型。但是当群体总数增大到一定程度时，上面方程中右端的第二项所产生的影响就不能忽略。

威尔霍斯特模型是将生物群体中每一个个体视为同等地位来对待的，而这个原则只适用于低等动物。对于人类群体来说，必须考虑不同个体之间的差别，特别是年龄因素的影响。人口的数量不仅和时间有关，还应该和年龄有关，而且人口的出生、死亡等都和年龄有关。不考虑年龄因素就不能正确的把握人口的发展动态。此时，我们必须给出用偏微分方程描述的人口模型：

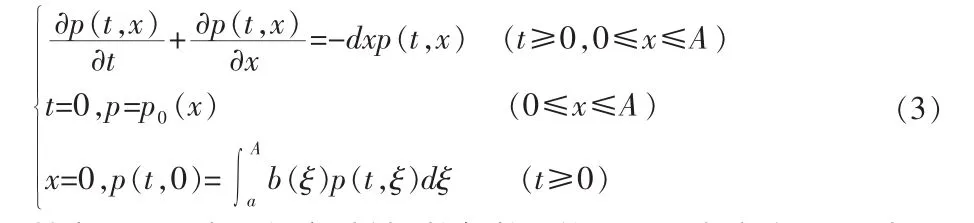
其中，p（t,x）表示任意时刻 t按年龄 x的人口分布密度，d（x）表示年龄为x的人口死亡率，b（x）表示年龄为x（ɑ≤x≤A）的人的生育率，ɑ表示可以生育的最低年龄，A表示人的最大年龄。

对于上述偏微分方程模型成立如下结论：

定理1：对偏微分方程的初值问题（3），如果下列条件成立：

（Ⅰ）在闭区间0到A上，p0（x）≥0且适当光滑；

（Ⅱ）在闭区间 0到A上，d（x）≥0且适当光滑，并且当 x→A-0时，d（x）趋近于无穷大及

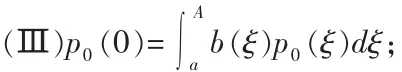
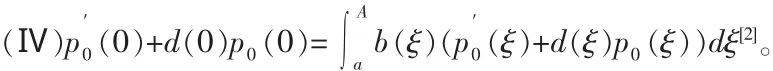
则该初边值问题（1）-（3）存在唯一的整体解 p（t，x）同时满足 p（t，x）≥0 且 p（t，A）＝0。

该模型在经过适当的简化假设后，例如假设 d（x）≡d＝常数，b（x）≡b＝常数，就可以回到常微分方程模型。但在偏微分方程模型中d＝d（x）、b＝b（x）均与年龄有关，这与现实情况相符。因此，偏微分方程模型确实更能精确地描述人口分布的发展过程。

3 结论

随着物理学、医学、生物学等学科所研究的现象在广度和深度两方面的不断扩展，偏微分方程的应用范围变得更加广泛。而从数学自身的角度来看，偏微分方程的求解促使数学在函数论、变分法、常微分方程、数值分析、微分几何等各方面均有不同程度的发展。所以从这个角度来说，偏微分方程变成了数学的中心。由于同一类型的偏微分方程往往可以用来描述许多性质上颇不相同的自然现象，所以对一些重要的偏微分方程开展研究，可以有许多方面的应用前景，并有望在新兴学科或边缘学科的开发中及时的发挥作用。

［1］吴方同.数学物理方程[M].武汉:武汉大学出版社,2001:18-36.

［2］朱长江,邓引斌.偏微分方程教程[M].北京:科学出版社,2005:106-112.

［3］李文林.数学史概论[M].北京:高等教育出版社,2002:19-26.

［4］陈祖樨.偏微分方程[M].合肥:中国科学技术大学出版社,2004:21-33.