正交小波滤波器系数和的合理性研究

杨正理

（三江学院，江苏 南京 210012）

0 引言

多分辨分析理论提供了构造正交小波的一个基本框架。其基本方法是：先构造一个满足多分辨率的嵌套闭子空间序列{Vj}j∈z,并使它构成整个L2(R)空间。在V0空间找一个函数φ(t),它的平移函数序列{φ(tk)}k∈z构成V0空间的Riesz基。特别指出，Riesz基仅能保证序列{φ(tk)}k∈z线性无关，但并不能保证其构成V0空间的一个标准正交基。一般的，我们可以对一个非正交的函数φ(t)通过正交化方法使其正交。则当 φ(t)∈V0时，序列{φ(t-k)}k∈z构成 V0空间的一个标准正交基，φj,k(t)＝2j/2φ(2jt-k),j,k∈Z构成Vj的一个标准正交基。于是，我们说φ(t)生成正交多分辨分析。这样就可以通过φ(t)的二尺度方程求出相应的滤波器系数{hk},并根据φ(t)和{hk}采用Mallat算法对正交小波进行分解与重构。

通过上述分析，滤波器系数{hk}是正交小波分析过程中十分重要的参数。然而，很多书藉及文献中对这个重要参数的总和却推导出了不同的结论。如文献[1-2]中推导出滤波器系数总和；而文献[3-5]中却推导出。这两种结论必然有一个是不合理的。这里仅用“不合理”而没有用“错误”来说明这一结论，是因为即使在得到不合理结论的文献中，并没有因为这个不合理结论而造成更多其它理论上的错误，原因在于这两个结论之间仅仅相差了一个的常倍数。但是，两种截然不同的结论往往给读者的阅读造成困惑，给学习者特别是初学者的理解带来不少困难。本文将对正交小波的滤波器系数总和这一结论的获得过程重新进行严格、完整的数学推导，从而得到一个合理的结论，以助学习者理解。之所以要重新完成该推导过程，是因为诸多文献中在涉及到这块内容时鲜有完整的推导和证明过程，也许正是这个原因疏忽了这个不合理结论的存在。

1 正交小波滤波器系数总和的合理结论推导过程

正交小波滤波器系数的总和需由正交小波分析的二尺度方程得到，所以推导过程需由二尺度方程的有关定义开始推导。本文中所涉及的有关多尺度逼近、二尺度方程及多分辨分析的相关定义及内容请参考相关文献。

由多分辨分析概念得知，如果φ(t)为尺度空间V0的一个标准正交基函数，其平移序列{φ(t-k)}k∈z构成V0空间的一个标准正交基，而对任意的 j,k∈Z，φj,k(t)＝2j/2φ(2jt-k)构成 Vj的一个标准正交基，则称 φ(t)为尺度函数。又由于V0⊂V1，所以φ(t)也必然属于V1空间，也即φ(t)必然可用V1空间的正交基φ1,k(t)线性展开(这里的φ(t)可认为是尺度函数在0尺度空间下，平移量j＝0时所得到的函数，故可用φ0,0(t)方式来表示其含义)：

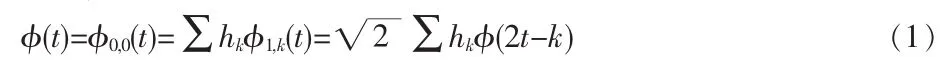
其中展开系数 hk＝＜φ(t),φ1,k(t)＞，也称低通滤波器系数。 由于式（1）描述的是相邻两个尺度空间基函数之间的关系，所次称此式为二尺度方程。

又由于 Vj⊂Vj+1，φj,0(t)∈Vj，所以 φj,0(t)也必然属于 Vj+1空间，也即φj,0(t)可用Vj+1空间的正交基φj+1,k(t)线性展开,如下：

其中展开系数 hk′＝＜φj,0(t),φj+1,k(t)＞，且有

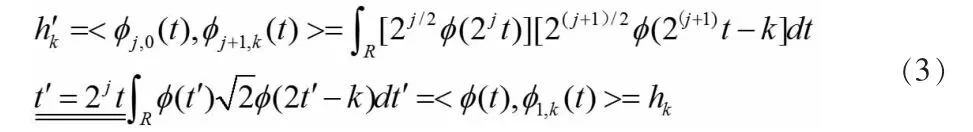
式（3）说明，正交小波的滤波器系数hk不随尺度j的变化而变化。即二尺度关系存在于任意相邻尺度j,j+1之间，那么式（1）与式（2）的表达式可统一为：

对式（4）两边同时对t积分得：

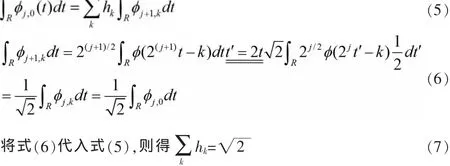
在式（1）两里边同时作Fourier变换，可得到二尺度方程的频域表示：

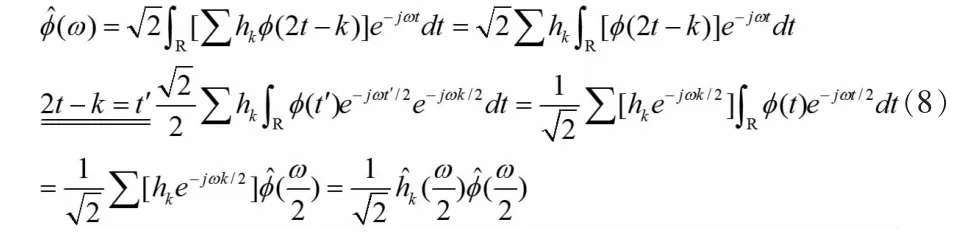
由式（8）得：

令 ω=0，由式（9）可得 ，将此式代入式(10),可得：

式（1）到式（11）的数学推导过程是严密而完整的，因而得到的式（7）和式（11）的结论也应该是完全合理的。 式（7）是从时域方面，式（11）是从频域方面，说明了正交小波的滤波器系数总和应为，在使用过程中应注意不要用错。

2 正交小波滤波器系数总和的不合理结论的产生原因

第1节中的数学推导过程分别从时域和频域两个方面得到了正交小波滤波器系数总和的结论，这也是各种文献得到该结论最常用的两种方法。而有些文献得到的不合理结论的原因也正是在这两种推导方法中产生的。

2.1 从时域方面得到不合理结论的过程

在多尺度逼近中，通常取 φj,k(t)＝φ(2jt-k)，特别是当 φj,k(t)具有内插基函数特点时，对构造各尺度空间Vj的近似函数fj十分便利。有的文献中直接采用该φj,k(t)定义出二尺度方程形式：

注意，式（12）表示的二尺度方程与式（4）比较差了一个√2，而这种二尺度方程格式在不少文献中均有采用。式（12）既表示了尺度空间V0和V1的关系，也表示了任意尺度空间Vj和Vj+1之间的传递关系，即可由式（12）得到更通用的二尺度方程：

根据式（1）至式（7）的推导过程可知，对式（13）两边同时积分可得到滤波器系数总和应该为2，即

2.2 从频域方面得到不合理结论的过程

从式（8）到式（12）的数学推导可知，对式（12）所表示的二尺度方程两边作Fourier变换，也能得到正交小波滤波器系数总和为2的结论，即。原因也在于式（12）的表达式与式（1）比较相差一个的倍数。

2.3 不合理结论的产生原因

通过对产生不合理结论的过程进行分析，无论从时域方面还是从频域方面得到不合理结论的根本原因都在于忽略了多尺度逼近定义与多分辨分析定义之间在条件之间存在着微小区别，从而采用了不合理的二尺度方程表达式，最终导致不合理结论的产生。关于多尺度逼近定义与多分辨分析定义之间在条件之间存在的区别可从以下两点进行说明：

（2）在多尺度逼近中，φ(t)∈V0⊂V1，虽然会隐含着 φ(t)可由{φ(2tk)}表示的事实，然而在多尺度逼近中常常考虑的是如何采用基函数对空间内函数进行逼近的情况，并不强调相邻尺度子空间Vj和Vj+1之间的联系。而在多分辨分析中，则重点强调二尺度方程式（4）是一种显式的线性关系，重点强调二尺度方程表述了任意函数子空间Vj间的递推关系，只有利用这种递推关系，才有著名的Mallat快速算法的实现。

如果没有注意到这些特点，从而混淆多尺度逼近及多分辨分析的基函数应用，而构造出不合理的二尺度方程，就会得到不合理的结论。

3 结语

本文从时域及频域两个方面对正交小波滤波器系数的总和这一结论进行了严格与详细的数学推导，不但十分明显的得到了正交小波滤波器系数总和应该为的结论，而且这一推导过程可对很多文献中的有关小波分析理论内容进行补充。同时，对有些文献中得到正交小波滤波器系数总和为2的不合理结论所产生的过程及原因进行了详细的分析与叙述，进而有力的验证了滤波器系数总和应为的结论。当然，本人仅仅从这种不合理的结论会造成读者学习困难的角度提出问题，对于这一不合理结论所造成的其它不良影响，希望同行们不吝赐教。

［1］杨正理.采用小波变换的周界报警信号辨识[J].光电工程,2013,1,278(40):84-89.

［2］杨正理,黄其新.小波变换在行驶车辆检测器中的应用研究[J].公路交通科技,2013,2,(206)2:104-108.

［3］杨正理.基于小波变换的模糊C-均值聚类算法在动态汽车衡中的应用[J].自动化仪表,2013,9(34)9:73-77.

［4］徐长发,李国宽.实用小波方法[M].2版.武昌:华中科技大学出版社,2004,1.

［5］任震,等.小波分析及其在电力系统中的应用[M].北京:中国电力出版社,2003,11.

［6］张德丰.MATLAB小波分析[M].北京:机械工业出版社,2010,1.

［7］Chaari O,Meunier M,Brouaye F.Wavelets:A New Tool for the Resonat Grounded Power Distribution Systems Relaying[J].IEEE Transactions on Power Delivery,1996,11(3):1301-1308.

［8］Qin-Jian,Chen-xiangxun et al.Travelling Wave Fault Location of Transmission Line Using Wavelet Transform.[C]//Electric Power Research Institute.POWERCON,98.Beijing:Wan Guo Xue Shu Publisher,1998,533-537.