多弱面地层水平井裸眼井壁垮塌量计算模型

刘志远，陈勉，金衍，杨向同，卢运虎，熊启泉

（1. 中国石油大学（北京）石油工程学院；2. 中国石油塔里木油田公司）

多弱面地层水平井裸眼井壁垮塌量计算模型

刘志远1，陈勉1，金衍1，杨向同2，卢运虎1，熊启泉1

（1. 中国石油大学（北京）石油工程学院；2. 中国石油塔里木油田公司）

针对裂缝性地层水平井试油过程中井壁垮塌的问题，建立了多弱面地层水平井裸眼井壁垮塌量计算模型，采用该模型分析了水平井裸眼井壁垮塌量的影响因素，并通过现场应用将其与单弱面模型进行对比分析。分析裂缝产状、井眼方位、地层应力各向异性、弱面数量及井内液体密度对井壁垮塌量的影响后发现：裂缝倾角较小时，井壁垮塌量较大，井壁稳定性差，裂缝倾角较大时，井壁垮塌量波动较大，井壁稳定性随井眼方位及裂缝倾向的变化而变化；裂缝倾向不同垮塌量极大值出现时井眼方位不同；地应力差越大井壁垮塌量越大；井壁垮塌量随井内液体密度的增加而减小，当井内液体密度在孔隙压力当量密度附近时垮塌量对井内液体密度的变化较敏感。现场应用结果表明：与单弱面模型相比，大多数情况下采用多弱面模型计算的井壁垮塌量更大，能更可靠地评估井壁垮塌风险。图13参16

多弱面；裂缝性地层；垮塌量；井壁稳定性；水平井

0 引言

裂缝性地层井壁围岩裂缝系统发育[1-2]，易造成井壁垮塌，针对该问题金衍等[3-7]做过大量细致研究，认为地层弱面及井眼方位对井壁稳定有重大影响。对于井壁失稳后的井眼破坏形状，Wu B等[8]和PapaMichos E等[9]通过实验研究认为岩石在井壁失稳时发生剪切破坏，破坏形状一般呈椭圆形。但对于井壁失稳后的垮塌量计算问题，上述研究者没有进行研究，并且在研究弱面破坏问题时没有考虑多弱面情况。Aadnoy B S等[10-11]通过理论分析建立了井壁垮塌量计算的简单模型，但该模型没有考虑弱面情况，不适用于裂缝性地层。因此，本文从力学机理出发，结合裂缝性地层裂缝发育特点，建立多弱面地层水平井裸眼井壁垮塌量计算模型，对裂缝性地层试油过程中水平井裸眼井壁垮塌量进行分析和预测。

1 多弱面理论

对于裂缝性地层，在工程实际中井壁往往出现多弱面同时存在的情况（见图1a），采用单一弱面条件对井壁垮塌量进行预测会出现偏差，本文以两组弱面模型（见图1b）为例，运用叠加原理对多弱面井壁稳定性进行评价和分析，忽略局部块体滑动造成的应力变化。两组弱面破坏后的强度叠加如图1c所示。

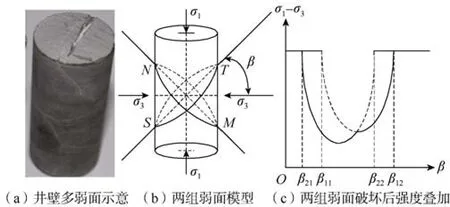
图1 多弱面理论示意图

采用摩尔库仑破坏模型，在单弱面[12]的基础上对多弱面破坏（见图2）进行分析，不同产状的弱面其形态和强度特征各不相同。

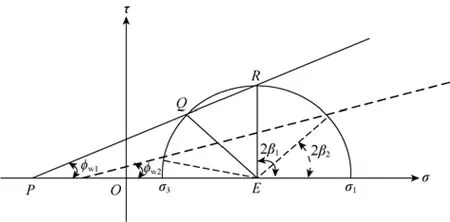
图2 多弱面破坏准则示意图

由弱面的强度线与摩尔应力圆的几何关系可得：

βi1和βi2分别为弱面破坏时βi的下限和上限值。由摩尔应力圆可知：当βi1＜βi＜βi2且满足（2）式条件时，井壁产生弱面破坏；当 0≤βi≤βi1或βi2≤βi≤π/2时，弱面稳定。

2 水平井裸眼井壁垮塌量计算模型

2.1 井眼破坏形状

裂缝性地层井眼在井壁稳定的情况下一般呈圆形，但地层应力各向异性[13]、孔隙压力、流体渗流、井壁温度场等产生的应力集中以及岩石强度[14]、裂缝发育程度、裂缝产状的影响会导致井眼变形。Papamichos E等[9]通过空心圆柱岩样的井壁稳定性实验研究发现，井壁失稳时，随着围压的增加破坏面积逐渐增大，破坏形状由最初的圆形向椭圆形过渡（见图3），该结果与Wu B等[8]的实验结果类似。

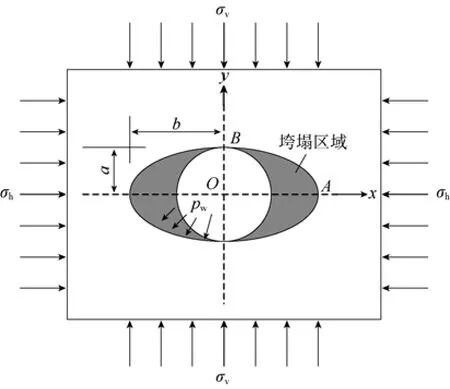
图3 变形前后的井眼形状

井周应力集中是井壁岩石坍塌掉块的根本原因之一[10]，井周各点应力集中差异越大、岩石强度越低、弱面越发育，则井壁出现垮塌的可能性越大。对于水平井，由于地层应力各向异性的影响，椭圆形井眼井周在地应力作用下所受的压缩切应力[15]为：

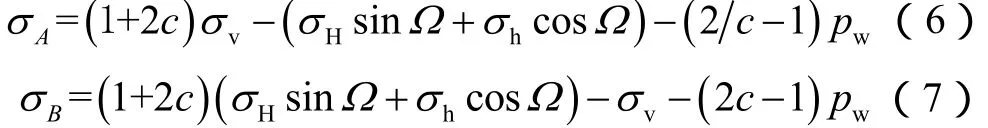
2.2 井周应力状态

视天然裂缝性地层为连续介质体，水平井井壁上应力分量在极坐标中可表示为[16]：

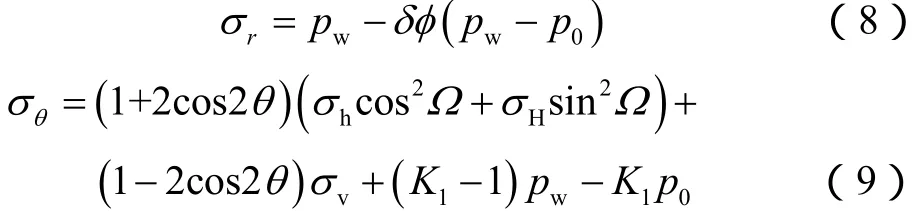
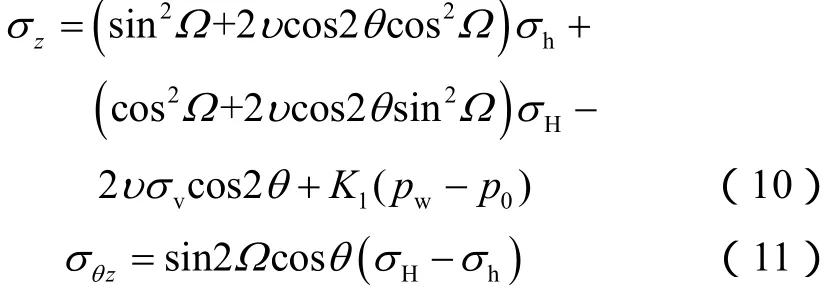
设井眼方位角为θZA，水平最大地应力方位角为θHA（Ω=θZA−θHA），θZA和θHA均以大地坐标系中的北东向来表示（见图4、图5）。

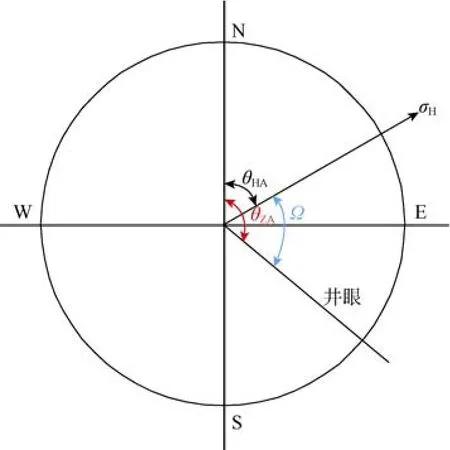
图4 大地坐标系下井眼方位及最大地应力方位

假设井壁泥饼完好，不考虑钻井液滤液的渗流效应，水平井柱坐标系中井壁上的最大、最小主应力可表示为：

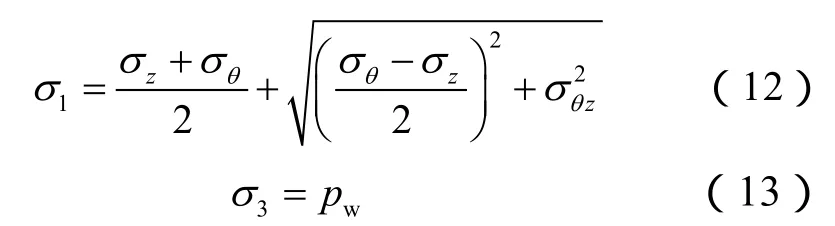
σ1的作用面与z轴的交角为：

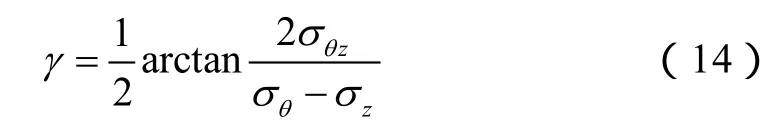
弱面i的法向与最大主应力σ1之间的夹角βi满足如下关系：

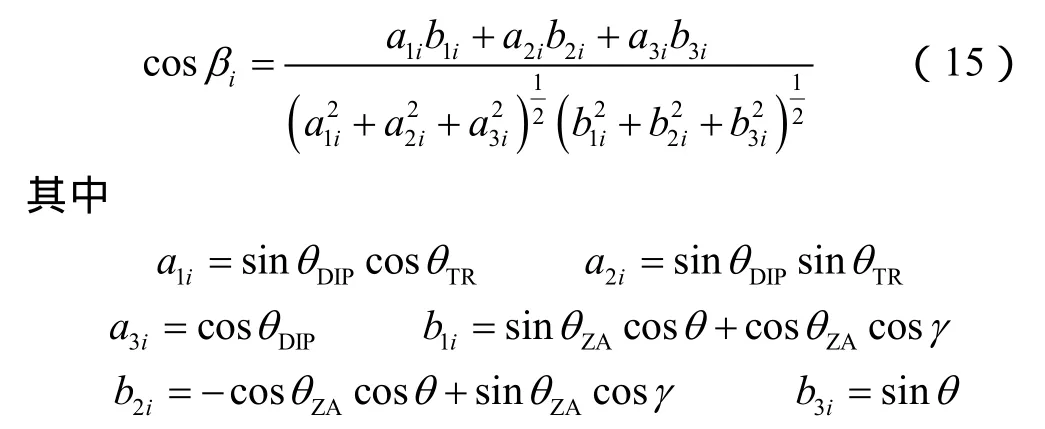
2.3 井壁垮塌量计算模型

由（12）式、（13）式可得井壁处最小有效主应力：

将（16）式代入（2）式得到井壁处最大有效主应力（即井壁坍塌破坏临界条件）为：

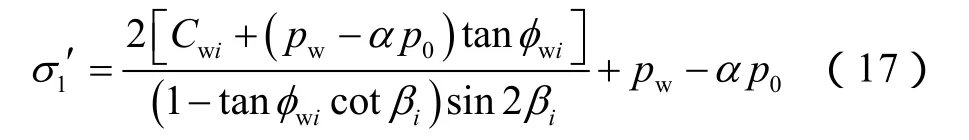
由（8）式—（11）式可知，当剪切应力σθz为零时，即σH=σh或Ω=0或θ=π/2时，水平井井周最大主应力[10]可表示为：

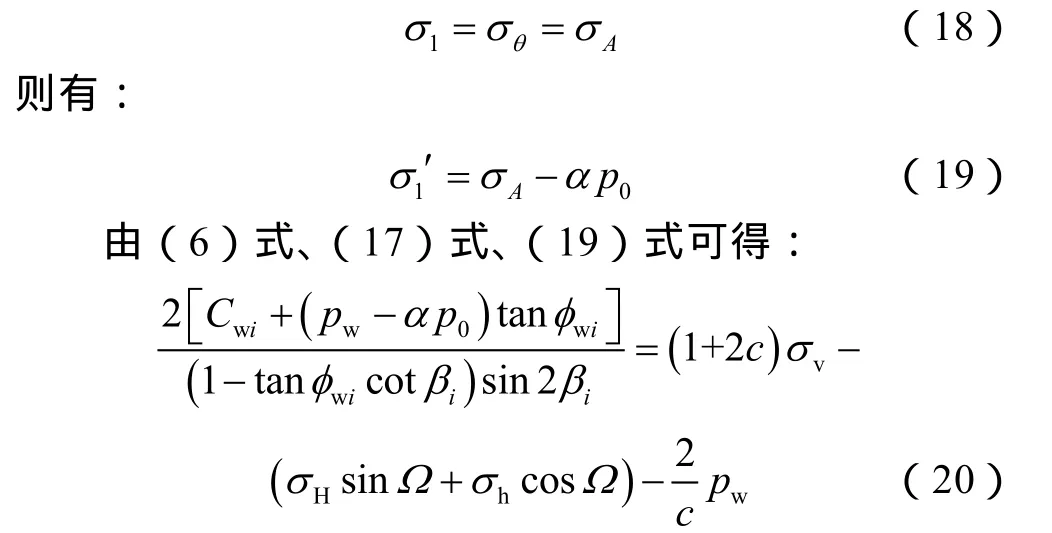
在井眼形状为圆形的初始条件下，井壁易在A点处发生垮塌，由（20）式可得：

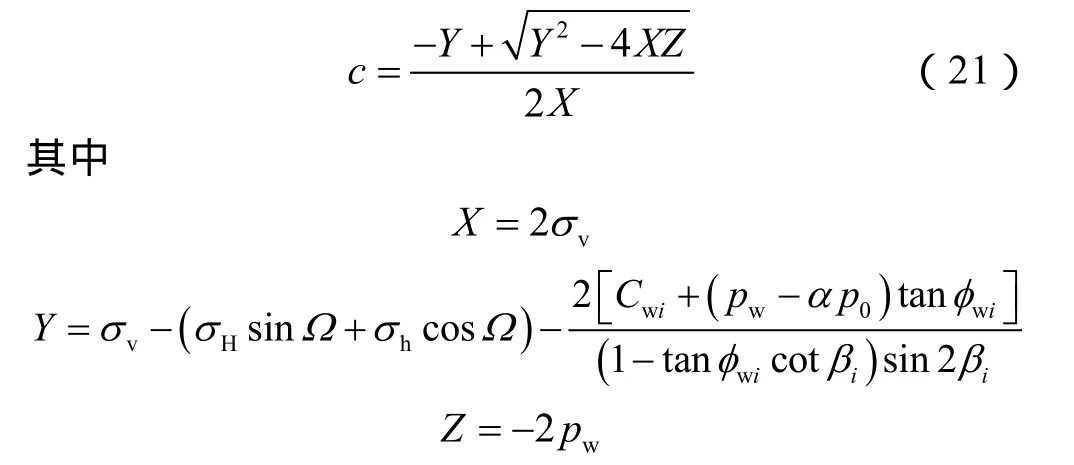
通过以上分析可知，井壁垮塌量为井眼垮塌前后的体积之差，即：

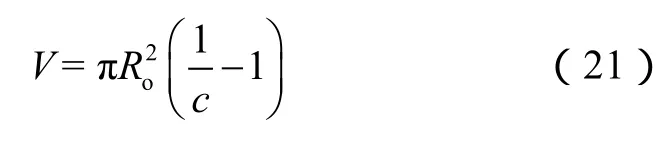
3 水平井裸眼井壁垮塌量影响因素

采用某油田奥陶系储集层地质力学参数对水平井裸眼井壁垮塌量的影响因素进行分析：井深6 300 m，单位井深上覆压力0.024 5 MPa，单位井深水平最大主应力0.022 0 MPa，单位井深水平最小主应力0.019 5 MPa，地层孔隙压力73 MPa，弱面黏聚力4 MPa，弱面内摩擦角15°，本体黏聚力20 MPa，本体内摩擦角35°，弹性模量38 GPa，泊松比0.24，比奥系数0.85，井眼直径152.4 mm，水平最大地应力方位角120°，地层平均孔隙度0.25，井壁渗透系数0.7，井内液体密度1.25 g/cm3。

3.1 裂缝产状及井眼方位

采用本文建立的井壁垮塌量计算模型分析了裂缝产状及井眼方位对水平井裸眼井壁垮塌量的影响（见图6—图9）。结果表明：①随着天然裂缝倾角的增加，井壁垮塌量的变化幅度增大。裂缝倾角较小（小于45°）时，井壁垮塌量较大，在0.014～0.016 m3/m波动，井壁稳定性差；裂缝倾角较大（大于等于45°）时，井壁垮塌量在0.002～0.016 m3/m波动，井壁稳定性随井眼方位及裂缝倾向的变化而变化。②裂缝倾角较大（大于等于45°）时，井壁垮塌量受井周弱面及应力集中两方面的影响，产生弱面破坏及本体破坏，且随着裂缝倾角的增加弱面破坏区间逐渐增大（见图7—图9红色区域），本体破坏区间逐渐缩小（见图7—图9浅绿色区域），即井壁不稳定性逐渐增加。③裂缝倾向对井壁垮塌量有显著影响。垮塌量极大值、极小值均集中在裂缝倾向为 45°～90°时，裂缝倾向不同极大值、极小值出现时的井眼方位也不同。④裂缝倾角小于等于60°，裂缝倾向为45°～90°及井眼方位在最大水平地应力方位附近时，或者裂缝倾角大于 60°，裂缝倾向为45°～90°及井眼方位在最小水平地应力方位附近时，井壁垮塌量较低，井壁较稳定。

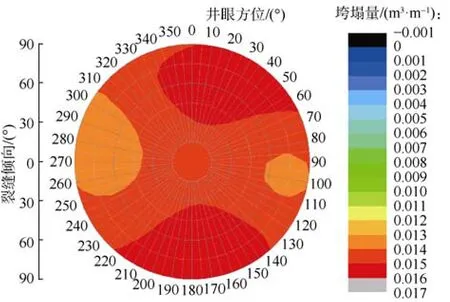
图6 裂缝倾角30°时井壁垮塌量与井眼方位、弱面产状关系

3.2 地层应力各向异性

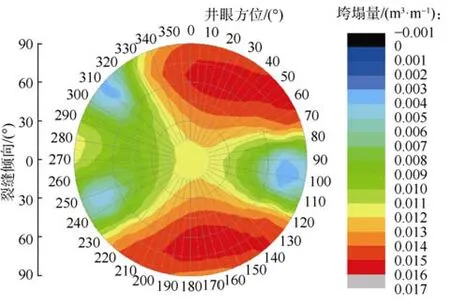
图7 裂缝倾角45°时井壁垮塌量与井眼方位、弱面产状关系

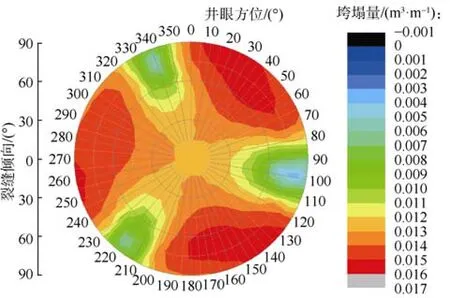
图8 裂缝倾角60°时井壁垮塌量与井眼方位、弱面产状关系

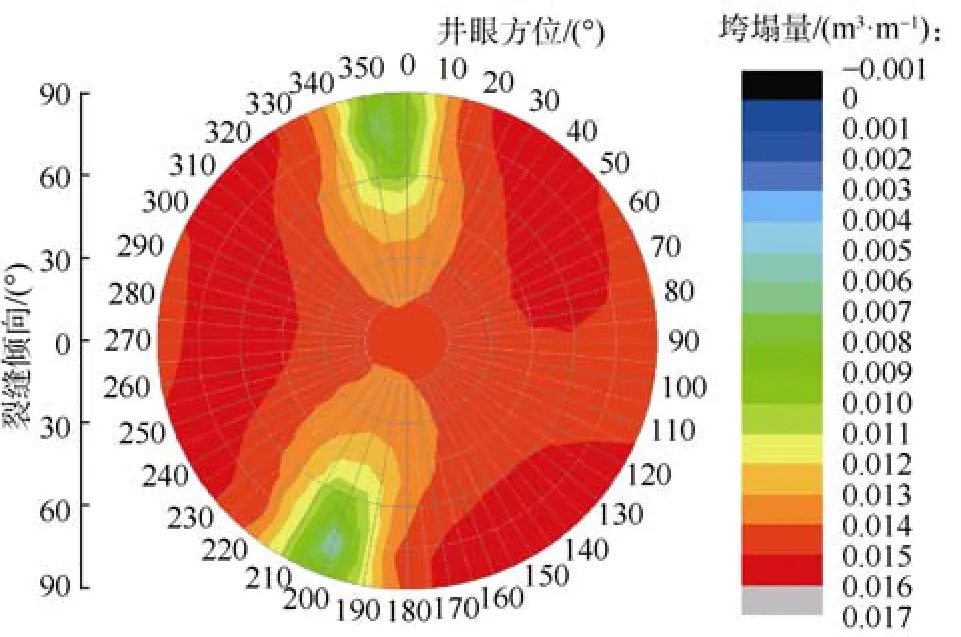
图9 裂缝倾角75°时井壁垮塌量与井眼方位、弱面产状关系

由（6）式、（7）式可知，地应力差越大，井壁应力集中越严重，井壁稳定性就越差。以裂缝倾角45°、倾向 60°时为例，通过不同的应力差系数（SF=σv/σh）研究地层应力各向异性对井壁垮塌量的影响（见图10）。结果表明：对于一定的井眼方位，当应力差系数从1.0逐渐增大到2.0时，井壁垮塌量逐渐增加。

3.3 弱面数量及井内液体密度

通过对1组弱面（裂缝倾角45°、倾向75°）和3组随机弱面（裂缝倾角45°、倾向75°；裂缝倾角60°、倾向45°；裂缝倾角75°、倾向15°）的情况进行对比，分析弱面数量（弱面发育程度）对井壁垮塌量的影响（见图11）。结果表明：对于裂缝性地层，大多数情况下采用单弱面模型计算的井壁垮塌量比采用多弱面模型计算的井壁垮塌量小。因此，采用多弱面模型能对井壁稳定性做出更可靠的评估。

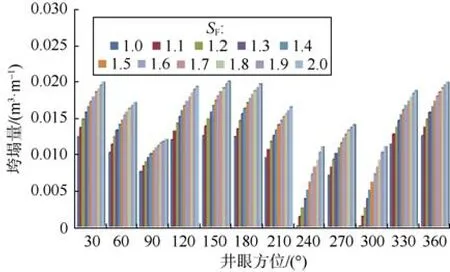
图10 地层应力各向异性对井壁垮塌量的影响

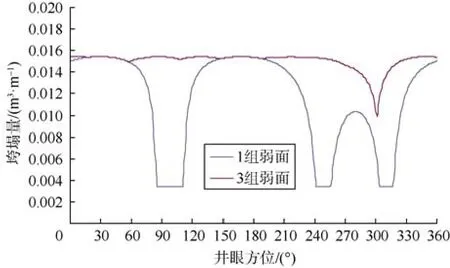
图11 弱面数量对井壁垮塌量的影响

此外，分析上述3组随机弱面情况及井眼方位60°时井内液体密度对井壁垮塌量的影响。结果表明：垮塌量随井内液体密度的增加而减小（见图12）；当井内液体密度在孔隙压力当量密度（1.18 g/cm3）附近时，垮塌量对井内液体密度的变化较敏感。

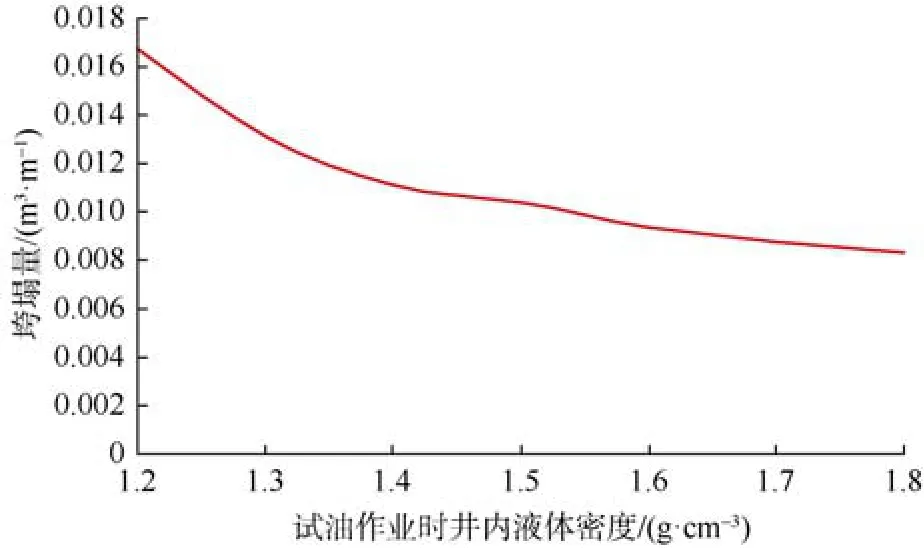
图12 井内液体密度对井壁垮塌量的影响

4 现场应用

中国内陆油田R井储集层属奥陶系，井深6 120 m，裂缝系统发育。该井在转试油后下试油完井一体化管柱，采用密度1.2 g/cm3的循环液，以0.27 m3/Min的循环速度反循环洗井，泵压较高且井口不出液，换装封隔器后上提1 100 kN活动解卡多次无效，倒扣起出管柱，井下埋卡管柱5根。现场分析认为，储集层垮塌，掩埋油层。

R井裸眼直径152.4 mm，试油油管直径88.9 mm。对裸眼垮塌段（井深6 070～6 120 m）的不同点，根据成像测井资料选取两组弱面参数，计算所需的其他剖面参数由测井数据和室内实验计算得到。各参数值为：单位井深上覆压力0.023 6 MPa，单位井深水平最大主应力0.021 0 MPa，单位井深水平最小主应力0.018 4 MPa，地层孔隙压力69 MPa，弱面黏聚力8 MPa，弱面内摩擦角22°，本体黏聚力24 MPa，本体内摩擦角38°，弹性模量44 GPa，泊松比0.23，比奥系数0.85，水平最大地应力方位角为 120°～160°，地层平均孔隙度0.25，井壁渗透系数0.7，裂缝倾角为60°～85°，裂缝倾向为30°～70°。

采用本文建立的井壁垮塌量计算模型进行双弱面叠加运算，选出垮塌井井深剖面上各点的垮塌量最大值，依次循环计算出垮塌剖面的垮塌量，并与采用单弱面模型计算的垮塌量进行对比分析（见图13）。

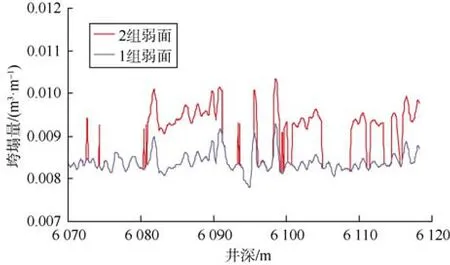
图13 R井裸眼垮塌段垮塌量

由图13可知：采用单弱面模型计算的R井裸眼垮塌段平均垮塌量为0.008 4 m3/m，而采用双弱面模型计算的平均垮塌量为 0.009 6 m3/m，后者比前者高出14%；从井深剖面来看，大多数情况下采用双弱面模型计算的垮塌量较大。结合R井的裂缝分布状态（非单弱面）及实际垮塌工况，采用双弱面模型预测的垮塌量也更符合实际，提高了垮塌风险预测的可靠度。

5 结论

本文结合裂缝性地层特点，基于多弱面理论，建立了多弱面地层水平井裸眼井壁垮塌量计算模型。

基于该模型对水平井裸眼井壁垮塌量影响因素进行分析后发现：①裂缝倾角较小（小于45°）时，井壁垮塌量较大，井壁稳定性差；裂缝倾角较大（大于等于45°）时，井壁垮塌量波动较大，井壁稳定性随井眼方位及裂缝倾向的变化而变化，随着裂缝倾角的增加井壁稳定性逐渐降低。②裂缝倾向对井壁垮塌量有显著影响，裂缝倾向不同垮塌量极大值出现时的井眼方位不同。③裂缝倾角小于等于60°，裂缝倾向为45°～90°及井眼方位在最大水平地应力方位附近时，或者裂缝倾角大于60°，裂缝倾向为45°～90°及井眼方位在最小水平地应力方位附近时，井壁垮塌量较低，井壁较稳定。④地层应力差越大井壁稳定性越差。⑤对于裂缝性地层，大多数情况下采用单弱面模型计算的井壁垮塌量比采用多弱面模型计算的井壁垮塌量小。⑥井壁垮塌量随井内液体密度的增加而减小，当井内液体密度在孔隙压力当量密度附近时垮塌量对井内液体密度的变化较敏感。

现场应用结果表明：与单弱面模型相比，采用本文建立的模型预测的井壁垮塌量更符合实际，提高了井壁稳定性评估的可靠度。

符号注释：

σ1，σ3——井壁处最大及最小主应力，MPa；β——弱面法向与σ1之间夹角，（°）；τ——切应力，MPa；σ——正应力，MPa；τβi——作用于第i组弱面的切应力，MPa；σβi——作用于第i组弱面的正应力，MPa；k——弱面数量；Cwi——第i组弱面的黏聚力，MPa；φwi——第i组弱面的内摩擦角，（°）；βi——第i组弱面的法向与σ1之间夹角，（°）；βi1，βi2——弱面破坏时βi的下限及上限值，（°）；σA——A点井壁集中应力，MPa；σB——B点井壁集中应力，MPa；σv——垂向应力，MPa；σh——水平最小地应力，MPa；σH——水平最大地应力，MPa；a，b——井壁垮塌后椭圆形井眼的短半轴及长半轴，m；c——a与b的比值；pw——井内液柱压力，MPa；Ω——相对于最大水平地应力的井眼方位，（°）；K1——渗流效应系数；σr，σθ，σz，σθz——水平井柱坐标系中的应力分量，MPa；θ——井周角，（°）；p0——地层孔隙压力，MPa；δ——井壁渗透系数；φ——地层平均孔隙度；α——比奥系数；υ——泊松比；Ψ——井斜角，（°）；θZA——井眼方位角，（°）；θHA——水平最大地应力方位角，（°）；γ——σ1的作用面与z轴的交角，（°）；θDIP——裂缝倾角，（°）；θTR——裂缝倾向，（°）；σ1′，σ3′——井壁处最大及最小有效主应力，MPa；Ro——井眼半径，m；V——井壁垮塌量，m3/m；SF——应力差系数。

[1] Seifi A, Kazemzadeh M B, Mohammadi H. 基于元建模的裂缝性气藏累计产量预测[J]. 石油勘探与开发, 2013, 40(2): 215-219.

Seifi A, Kazemzadeh M B, Mohammadi H. Prediction of accumulated outflow from a fractured hydrocarbon reservoir using metamodeling[J]. Petroleum Exploration and Development, 2013, 40(2): 215-219.

[2] 杨锋, 朱春启, 王新海, 等. 库车前陆盆地低孔裂缝性砂岩产能预测模型[J]. 石油勘探与开发, 2013, 40(3): 341-345.

Yang Feng, Zhu Chunqi, Wang Xinhai, et al. A capacity prediction model for the low porosity fractured reservoirs in the Kuqa foreland basin, NW China[J]. Petroleum Exploration and Development, 2013, 40(3): 341-345.

[3] 金衍, 齐自立, 陈勉, 等. 水平井试油过程裂缝性储层失稳机理[J]. 石油学报, 2011, 32(2): 295-298.

Jin Yan, Qi Zili, Chen Mian, et al. A mechanism study on the fractured reservoir instability during w ell testing of horizontal wells[J]. Acta Petrolei Sinica, 2011, 32(2): 295-298.

[4] 金衍, 陈勉. 钻前井壁稳定预测方法的研究[J]. 石油学报, 2001, 22(3): 96-99.

Jin Yan, Chen Mian. Study on prediction for borehole stability before drilling[J]. Acta Petrolei Sinica, 2001, 22(3): 96-99.

[5] 金衍, 陈勉. 利用地震记录钻前预测井壁稳定性研究[J]. 石油学报, 2004, 25(1): 89-92.

Jin Yan, Chen Mian. Prediction of borehole stability by seisMic records[J]. Acta Petrolei Sinica, 2004, 25(1): 89-92.

[6] Jin Y, Chen M, Chen K P. Pre-Caspian basin wells in salt-gypsum beds require an optiMized drilling fluid[J]. Oil & Gas Journal, 2011, 108(4): 46-53.

[7] Jin Y, Chen K P, Chen M. Development of tensile stress near a wellbore in radial porous media flows of a high pressure gas[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1313-1319.

[8] Wu B, Choi S K, Tan C P. Effect of stress anisotropy on cavity strength and implications in wellbore stability and sand production analyses[C]//Proceedings of the 40th US SymposiuMon Rock Mechanics. A lexandria, Virginia: American Rock M echanics Association, 2005.

[9] PapaMichos E, Stenebråten J, Cerasi P, et al. Rock type and hole failure pattern effects on sand production[C]//Proceedings of the 42nd US Rock M echanics Symposium. A lexandria, Virginia: American Rock Mechanics Association, 2008.

[10] Aadnoy B S, Kaarstad E. Elliptical geometry model for sand production during depletion[R]. SPE 132689-MS, 2010.

[11] Aadnoy B S, Kaarstad E. History model for sand production during depletion[R]. SPE 131256-MS, 2010.

[12] 沈明荣, 陈建峰. 岩体力学[M]. 上海: 同剂大学出版社, 2006.

Shen Mingrong, Chen Jianfeng. Rock mass mechanics[M]. Shanghai: Tongji University Press, 2006.

[13] Jin Y, Qi Z L, Chen M. Time-sensitivity of the Kaiser effect of acoustic eMission in limestone and its application to measurements of in-situ stress[J]. Petroleum Science, 2009, 6: 176-180.

[14] Jin Y, Yuan J B, Chen M, et al. DeterMination of rock fracture toughness K IIC and its relationship with tensile strength[J]. Rock Mechanics and Rock Engineering, 2011, 44: 621-627.

[15] Likhnitskii S G. Anisotropic plates[M]. Tsai S W, Trans. New York: Gordon and Breach, 1968.

[16] 陈勉, 金衍. 石油工程岩石力学[M]. 北京: 科学出版社, 2008.

Chen Mian, Jin Yan. Petroleum related rock mechanics[M]. Beijing: Science Press, 2008.

Calcu lation Model for bore-hole collapse volum e of a horizontal openhole in Mu ltiple-weak-plane form ation

Liu Zhiyuan1, Chen Mian1, Jin Yan1, Yang Xiangtong2, Lu Yunhu1, Xiong Qiquan1
(1.Faculty of Petroleum Engineering,China University of Petroleum,Beijing102249,China; 2.PetroChina TariMoilfield Company,Korla841000,China)

In view of borehole collapse in testing of horizontal wells, a calculation model for borehole collapse volume of horizontal open-hole in multiple-weak-plane formation was set up to analyze the factors affecting collapse volume. It was compared with the single-weak-plane model by field application. A fter analyzing the influences of fracture occurrence, well-bore azimuth, in-situ stress anisotropy, number of weak planes and fluid density on well-bore collapse volume, this study reveals: When the fracture dip is small, the volume of well-bore collapse is big and the well-bore stability is poor; When the fracture dip is big, the collapse volume varies greatly with the change of well-bore azimuth and fracture trend; The maximum collapse volume appears with different well-bore azimuth if fracture trend is different; The greater the in-situ stress difference is, the greater the well-bore collapse volume w ill be; The collapse volume decreases with the increase of borehole fluid density, and is more sensitive to the change of fluid density when fluid density is near the equivalent density of pore pressure. Field application results show that, compared with the single-weak-plane model, the multiple-weak- plane model gets big collapse volume in most cases so it can assess the collapse risk more reliably.

multiple weak planes; fractured formation; collapse volume; borehole stability; horizontal well

国家科技重大专项“塔里木盆地库车前陆冲断带油气开发示范工程”（2011ZX05046）

TE243

A

1000-0747(2014)01-0102-06

10.11698/PED.2014.01.13

刘志远（1984-），男，湖北天门人，现为中国石油大学（北京）石油工程学院博士研究生，主要从事石油工程岩石力学、井壁稳定与压裂技术等方面的研究工作。地址：北京市昌平区府学路18号，中国石油大学（北京）中油大厦812室，邮政编码：102249。E-mail：jiny@cup.edu.cn

2013-04-28

2013-11-14

（编辑 胡苇玮 绘图 刘方方）