一种求解TSP 问题的改进蚁群算法
2014-01-03冯月华
冯月华
(定西师范高等专科学校,743000)
蚁群算法是一种新型的启发式仿生类并行智能进化算法,最早是由意大利学者M.Dorigo 于1991 年首次提出,由于该算法具有分布式计算、正反馈机制以及较强的鲁棒性(容易与其他算法结合)等优点,在许多领域的组合优化问题的求解上得到了巨大的应用和成功。但基本的蚁群算法也存在着许多缺点,其中最关键的问题之一就是“探索”和“利用”之间的矛盾:既要以信息素的正反馈机制和启发因子引导整个蚁群逐渐向最短路径靠近,也就是利用先验信息快速搜寻最优解,提高收敛速度;但还要鼓励“探索”,以免收敛速度过快导致算法陷入局部最优解。针对算法缺点,学者们提出了许多改进策略:如M.Dorigo 提出的无论全局搜索能力还是收敛速度都有明显提高的蚁群系统(Ant Colony System,ACS);额外强化每次迭代的中找到的最优解的信息素浓度以提高收敛速度的带精英的蚁群算法(Ant System with Elitist Strategy,ASelit),但是该算法陷入局部最优解时很难跳出来;针对该问题,Stutsle T. 提出了最大最小蚁群算法(Max-Min Ant System,MMAS),将各边的信息素控制在( , )范围之内,并且只对每次迭代中产生的最短路径的信息素进行更新,使得搜索有效地控制在最短路径附近,从而更容易找出最优解,有效的防止“早熟”和“停滞”问题;还有将信息素动态更新的改进算法以及模拟真实蚂蚁,将蚂蚁设计成有分工、分类的多态蚁群算法。
1 算法改进策略
1.1 蚁群移动规则
在基本的蚁群算法中,如果到几个城市的信息量相差无几,让蚂蚁根据概率公式选取下一次要搜索的较优城市是十分困难的。因此对概率公式做了如下改进:
蚂蚁K 从城市i 转移到下一个城市j 的概率为:
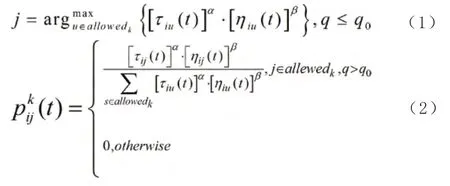
其中,q0先给定的(0,1)之间的参数,q 是在0~1 之间的随机数,当q> q0采用随机性搜索,按照公式(2)计算概率,从中选择其值最大的一条路径;当q<=q0时,蚂蚁采用确定性搜索,按公式(1)选择距离短且信息量多的路径,这种利用先验信息指导路径选择的策略提高了算法的收敛速度。q0调节了“利用”和“探索”之间的平衡,因此它的取值十分重要: q0的取值过大,大多数蚂蚁就会选择同一条路径(不一定是全局最优解),算法容易陷入局部最优解;如果取值过小,搜索就会变得很盲目,这样算法的收敛速度就会受到影响。因此,通常情况下, q0的前期取值为0.5,后期取值为0.9。
1.2 信息素的更新策略改进
为了不使启发因子被残留信息量淹没,在每次搜索结束后,要将残留信息素进行更新。带精英策略的蚁群算法的信息素的更新方法为:

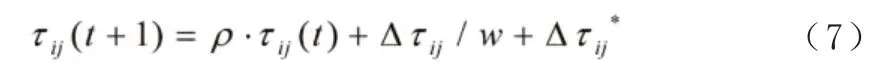
在搜索后期,蚁群已经接近全局最优解的时候, 的值已经足够大,该路径上的信息素的总和也已经足够多,并且算法的收敛速度也够快,再继续增加信息量的意义不是太大了,而且这个时候收敛速度过快反而降低了蚁群在已知最优解周围探索的能力,因此将(6)式中的 的值修改为:

1.3 信息素的自适应更新策略
蚁群算法研究的一个核心问题就是在“探索”和“利用”之间寻找一个平衡点。为信息素的挥发因子,当过小时,路径上的信息素过高,导致全局搜索能力过低;当过大时,路径上的残留信息素过低,算法的收敛速度就会变慢。改进算法用下式的自适应策略调节:
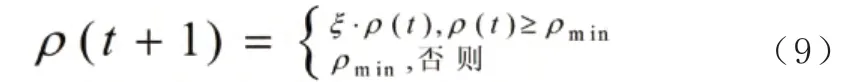
1.4 禁忌策略的改进
在许多改进的蚁群算法中很容易出现停滞状态:算法在当前的最短路径附近搜索了很多次,但最优解并没有更新,在这种情况下可以说明全局最优解并不在附近,然而算法却不能及时跳出。再建立一个禁忌表禁忌掉搜寻了很多次而最短路径没有更新的路径及附近路径,然后转到其他路径上继续搜索。在没有禁忌掉的其他所有路径中,找出最短路径继续搜索,如果新的最短路径比刚才禁忌掉的路径更优,为了充分利用先验知识、加快收敛速度,再将新的最短路径的信息素作为全局最短路径来更新。
1.5 算法步骤
改进算法求解TSP 问题的步骤如下:
Step1:初始化
设NC=0、MaxNc=5000,计算任意两个城市之间的距离,得到启发因子的初始矩阵;对所有边Lij 上的信息素赋初值;将m 只蚂蚁放置在n 个城市上,并更新对应的禁忌表;
Step3:判断蚂蚁是否访问完所有城市,计算每只蚂蚁的路径长度;否则转到step2 继续搜索;
Step4:选出最短路径,按照公式对信息素进行更新,并对路径上的信息素进行调整;
Step5:如果N 次循环中最短路径没有改进,将此路径和其附近路径置入禁忌表;
Step6:判断是否满足条件,满足条件输出;如果不满足条件,转到step2。
2 实验仿真
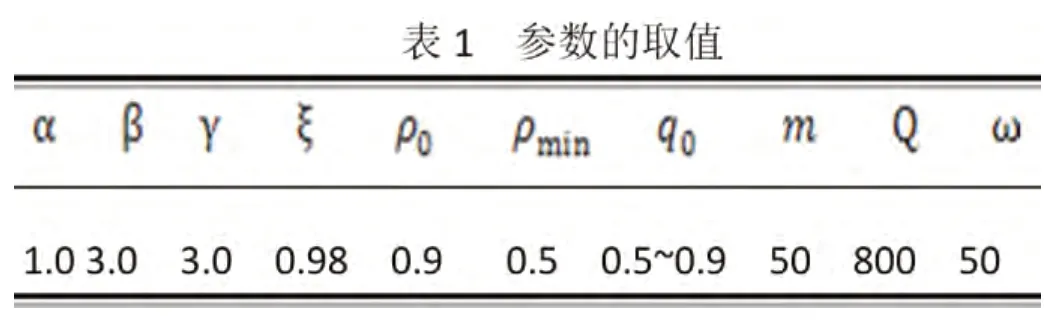
为了证明算法的有效性,采用TSPLIB 库中的eil51 问题进行测试,通过Matlab 编程,并在Intel 2.0G 的CPU、1G 内存的计算机上运行,试验参数为表1 所示。
?
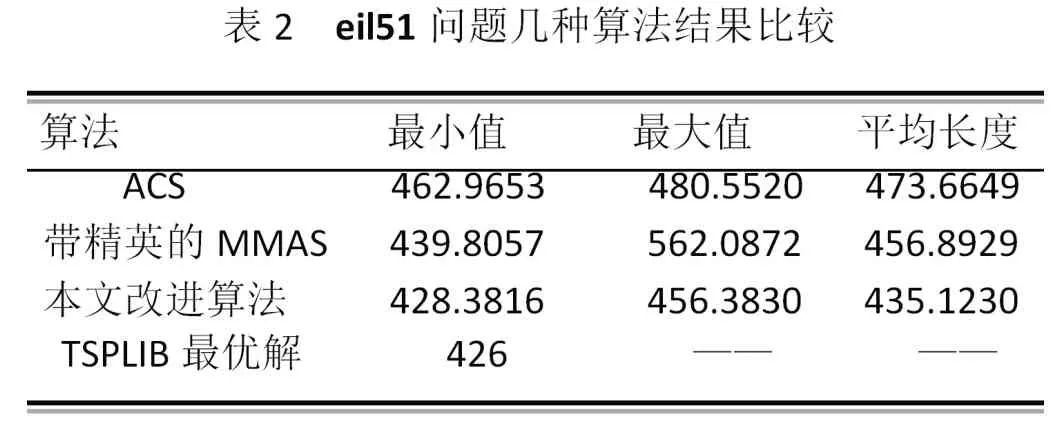
eil51 算例中包含51 分城市,算法对其运算的结果为表2 所示,通过40 次独立运行的实验结果数据与ACS 以及带精英的MMAS 算法相比较,表明本文改进算法得到的解更优,算法更稳定。图1 为改进算法得到的最优解的搜索图。
?
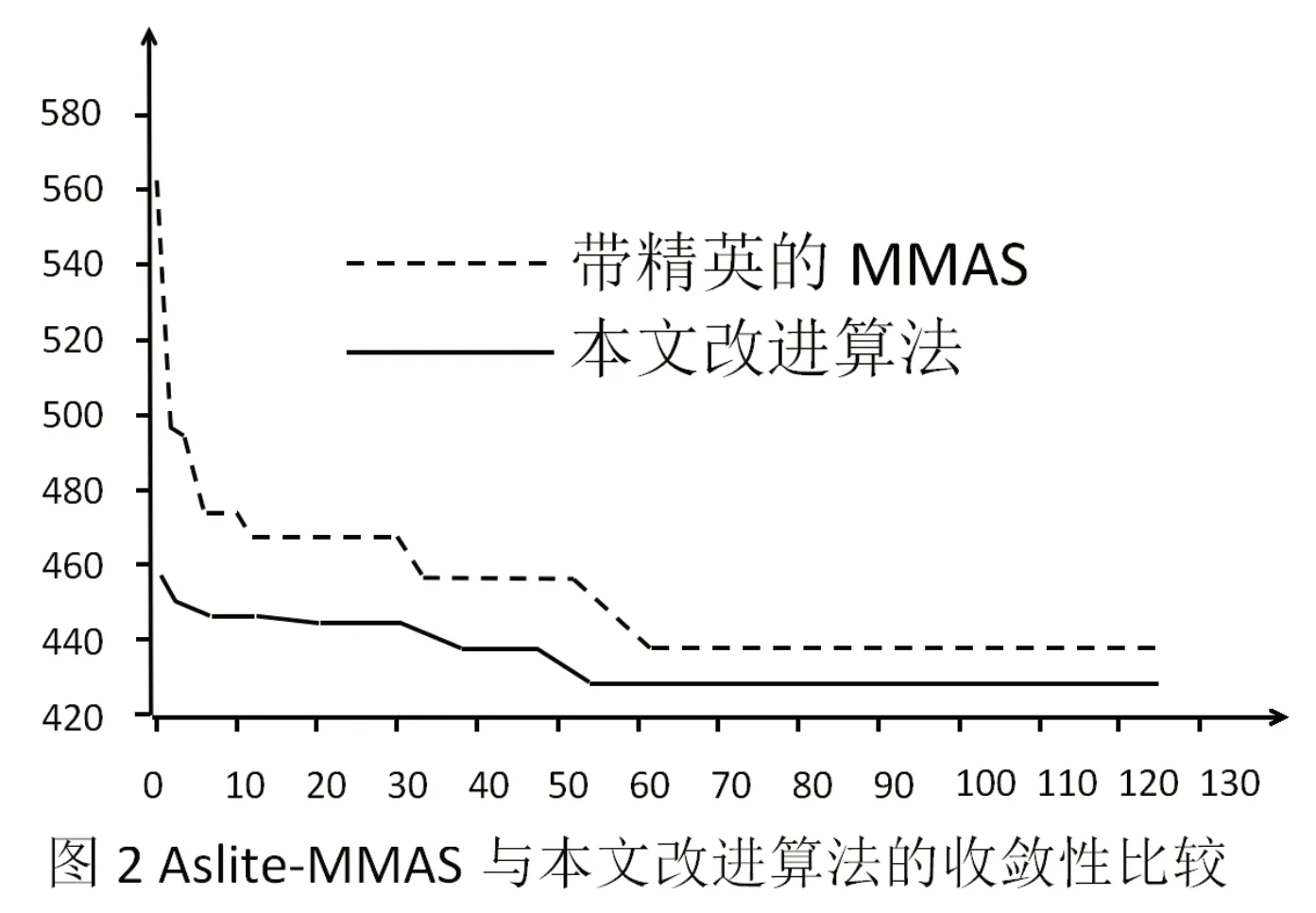
图2 是改进算法和带精英的最大最小算法收敛性能的比较,改进算法在30 次后基本收敛,最差收敛到456,最好收敛到428。在求解过程中两种算法都能朝全局最优解能不断收敛,但改进算法的收敛速度更快一些,得到的最优解更优,因此,与带精英的MMAS 相比,改进的蚁群算法更优。
3 结论
本文在带精英的MMAS 的基础上对蚁群算法从信息素动态调整策略、禁忌策略上做了进一步改进,实验证明改进算法更优,更稳定。但是改进算法在大规模的TSP 问题中寻优能力就会有所减弱,如何改进该问题以及对算法中采用怎样的参数自适应调整策略能进一步提高算法性能,还有待于进一步研究。
[1] 郭平,鄢文晋.基于TSP 问题的蚁群算法综述[J].计算机科学,2007.35(10):181~184
[2] BULLNHEIMER B,HARTL R F,STRAUSS C.A new rank based verion of the ant system:a computational study[R].Vienna.University of Vienna,1997
[3] STUTZLE T,HO0S H H.MAX-MIN ant system[J]. Future Generation Computer System,2000.16(8): 889-914
