定速感应风力发电机组的等效建模探究
2014-01-03龚广京
龚广京
(河海大学能源与电气学院,江苏南京,211100)
0 引言
分析风力发电机组对接入系统的暂态影响,需要建立机组的模型。定速感应风力发电机组(FSIG)由风力机、传动轴及齿轮箱、笼式异步发电机和无功补偿电容组成,机理复杂,建立详细的模型比较困难。系统辨识法将被研究系统当作黑箱,重点拟合系统外特性,适用于复杂系统。因此,本文基于系统辨识法,建立定速感应风力发电机组等效模型,采用粒子群优化算法辨识模型参数,并在MATLAB 中进行仿真验证。
1 定速感应风力发电机组的等效模型结构
研究风电机组对接入系统的暂态影响时,只需计及电网故障发生前一瞬间风电机组承受的风速,由于暂态过程较短,可以忽略风速的变化。因此,只需建立反映风电机组并网点电压和输出功率的关系模型。
本文将电力系统励磁模型应用到风电系统,等效模型建构如下所示:
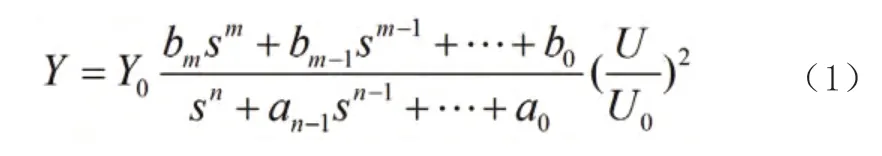
式中:m ≤n,bm、bm-1、…、b0、an-1、…、a0为常系数;Y为风电场输出的有功功率或无功功率;Y0为风电场输出的有功功率或无功功率稳态值;U 为风电场并网点电压;U0为电压稳态值。
2 基于粒子群优化算法的参数辨识
2.1 粒子群优化算法原理
粒子群算法(PSO)是模拟自然界中鸟群觅食行为而研发出的一种智能优化算法。采用粒子群算法解决问题时,每个优化问题的解分别由搜索空间中的一个粒子表示,所有的粒子都有一个被优化的函数决定的适应值,并有一个速度向量控制每个粒子飞行的方向和距离,所有粒子通过跟踪当前的最优粒子在解空间中搜索最优解。
假设在一个D 维搜索空间中,n 个粒子组成一个群体,第i个粒子在D 维搜索空间中的位置和速度分别表示为:

在每次迭代过程中,每个粒子在搜索过程中都
要考虑两个最优值:一个是各粒子迄今为止搜索到的最优值;另一个是全部粒子在整个空间中搜索到的最优值。分别表示为:

则在下次迭代中,粒子的速度和位置向量迭代公式如下:
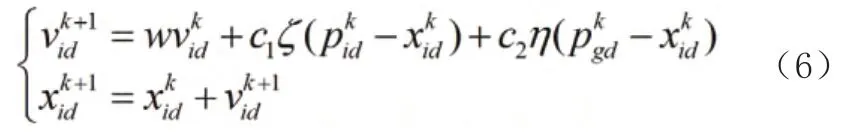
式中:i=1,2,…,n;d=1,2,…,D;k 是当前迭代次数; c1、c2为加速因子,分别表征粒子在向个体极值和全局极值靠近过程中的调整权重;w 是惯性权重,反映上次迭代中粒子速度对本次迭代中粒子速度的影响;ζ 和η 为[0,1]上均匀分布的随机数,用来保证群体的多样性。
2.2 参数辨识原理
非线性系统参数辨识的方法主要以优化为主,寻找一组最优参数向量θ*,使得误差函数值E 达到最小。在定速感应风力发电机组等效模型中,待辨识参数为bm、bm-1、…、b0、an-1、…、a0,设立误差函数为:式中:N 为采样点数量;n 为等效模型的阶次;Ym为实际观测的有功或者无功功率值(即真实值);Y 为等效模型的有功或无功功率值,θ 为待辨识的参数。
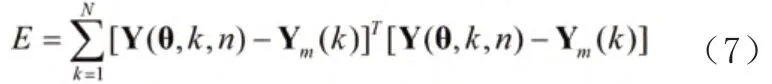
将误差函数作为粒子群的适应函数,并利用实际观测的并网点端电压和输出功率数据,就可以对其进行优化求解。利用粒子群优化算法辨识等效模型参数的原理如图1 所示。

图1 等效模型辨识原理Fig. 1 Schematic of equivalent model identification
2.3 基于粒子群优化算法的参数辨识步骤
由于粒子群优化算法是一种启发式的随机搜索算法,所以每次会得到不同的最优值。因此为降低随机性的影响,本文以多次计算误差函数后所得的平均值作为最终的评价指标。
为确定模型的阶次,由低到高依次计算各阶次模型的最优参数θ*及误差函数值E(n),通过比较不同阶次下E 的值,确定等效模型的最优阶次。具体步骤如下[6]:
1) 设定等效模型的阶次范围及各模型阶次下的计算次数;
2) 初始化粒子群算法的各参数值,包括粒子群的规模、加速因子、惯性权重、迭代次数、搜索空间,并初始化粒子空间的位置向量和速度向量;
3) 根据误差函数(7)计算所有粒子初始适应度,即误差函数值;
4) 根据式(6)更新各粒子的位置、速度和适应度,并找到当前个体最优值和全局最优值;
5) 判断是否达到设定的最大迭代次数,如果没有则返回至步骤4,如果已经达到最大迭代次数,则转至步骤6;
6) 根据式(7)计算误差函数值E;
7) 判断是否已达到设定的算法次数,如没有则返回至步骤2,如果达到转至步骤8;
8) 计算全部算法执行次数下E 的平均值。
9) 判断设定的阶次是否全部计算结束,如没有则返回至步骤1,如果结束转至步骤10;
10) 通过比较不同阶次对应的E 的平均值,确定等效模型的最优阶次,进而得出等效模型中的参数。
3 仿真实验
本文采用MATLAB/Simulink 中的FSIG 风电场模型进行仿真验证,见图2。风电场等值机由6 台容量为1.5MW 的FSIG 风力发电机组成,风电场出口处带有400KVar 无功补偿电容,故障点设置在25KV 与120KV 单回线路的正中间,路线长度为20km。
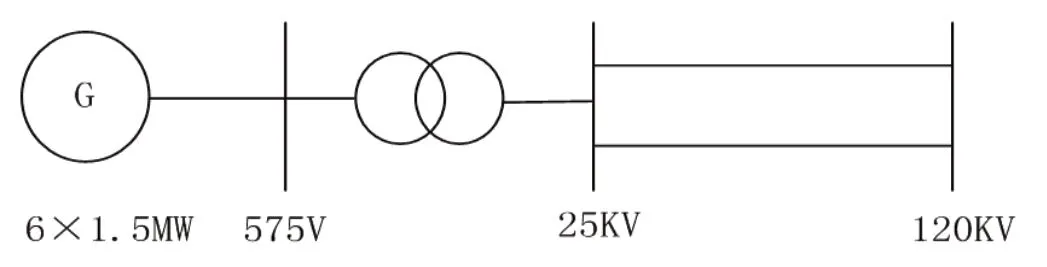
图2 算例系统Fig. 2 System scheme
设定等效模型的阶次范围为1 至5 阶,在每种阶次下,分别运行算法15 次,然后计算误差函数E 的平均值。通过比较E 的平均值确定模型的最优阶次。
输入风速保持恒速6m/s,系统120KV 高压输电线路中点设置三相短路故障,故障持续时间为0.1s,故障引起系统PCC 处电压跌落0.05pu,电压扰动如图3 所示。将PCC 电压作为输入变量,风电场输出有功、无功功率作为输出变量,辨识得等效模型参数如表1 所示,模型最优阶次为3 阶。图3 为详细模型与等效模型输出的仿真结果。
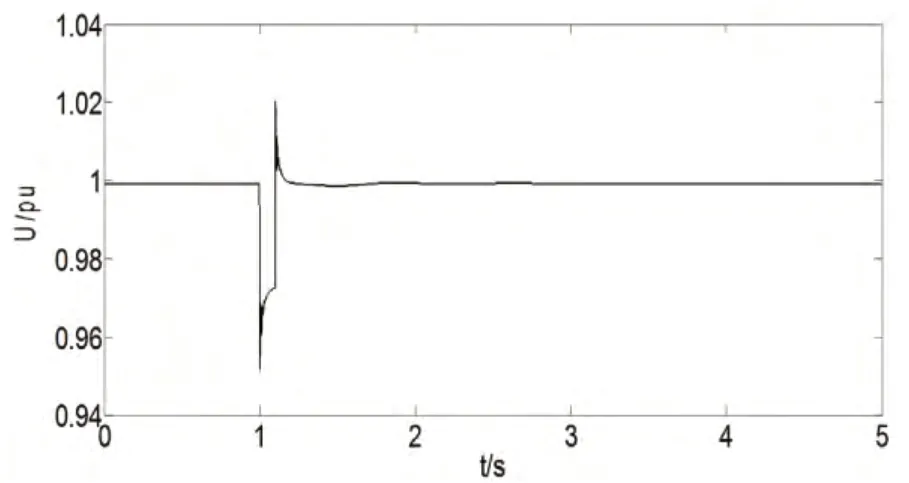
图3 扰动电压Fig. 3 voltage disturbance
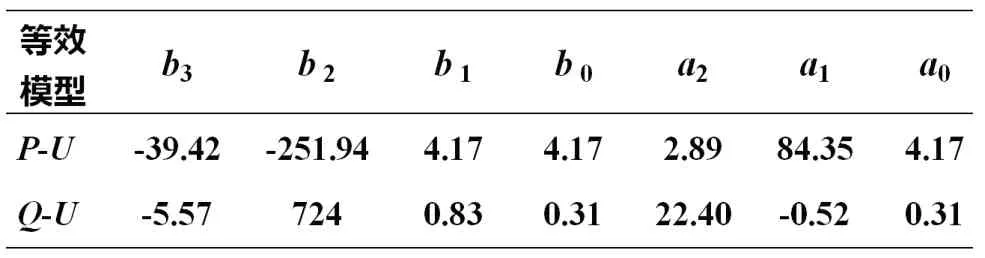
表1 参数的辨识结果Table. 1 Estimation result
由图4 可见,等效模型和实际模型的动态响应曲线基本保持一致,有功和无功的变化几乎重合。有功误差ε=2.96%,无功误差ε=2.65%,满足误差要求。
4 结论
本文针对FSIG 风力发电机组,以并网电压作为输入变量,输出功率为输出变量,采用粒子群优化算法,建立了定速感应风力发电机组等效模型,通过仿真验证了等效模型的准确性。
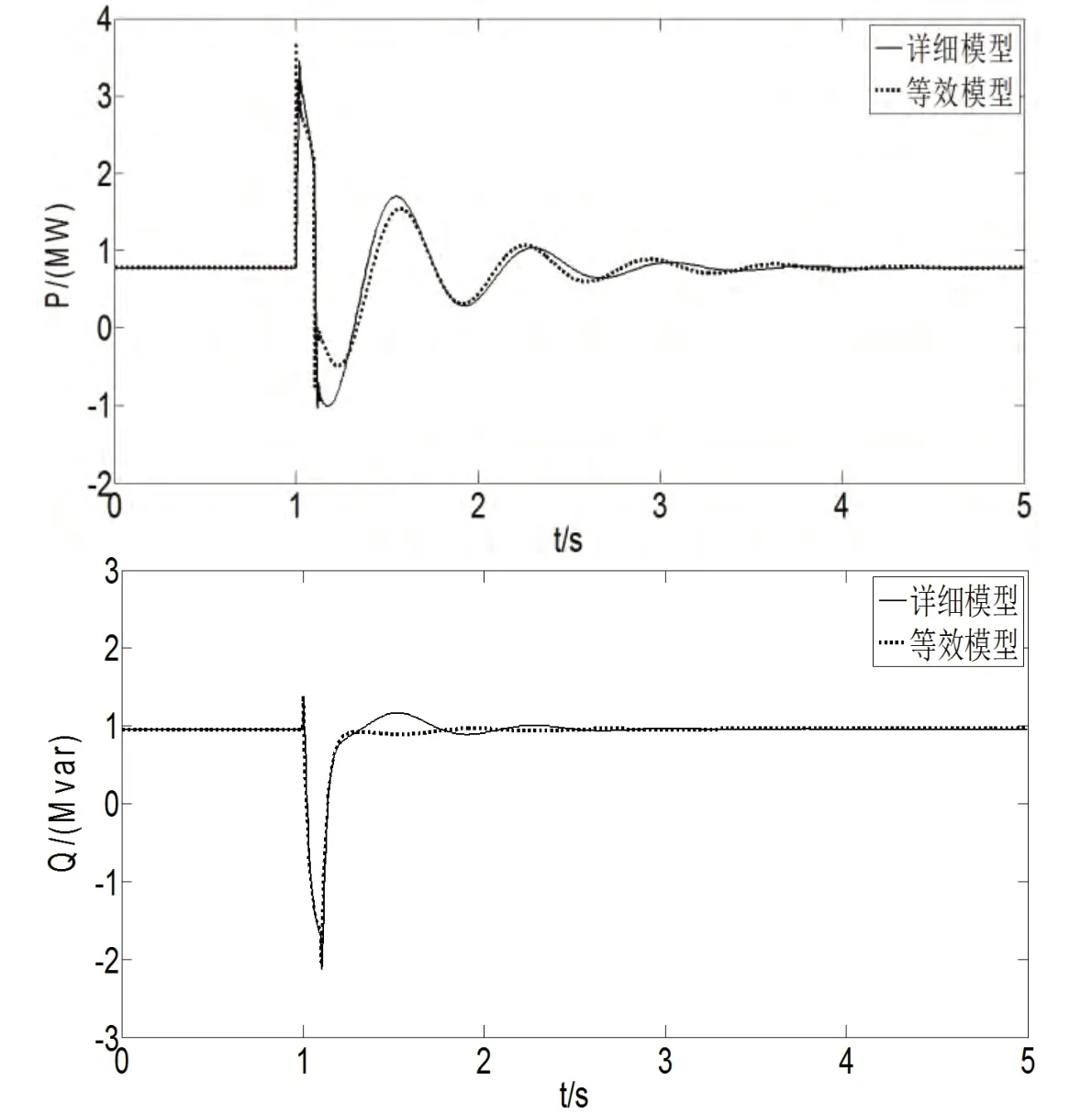
图4 电网故障扰动动态响应曲线Fig. 4 dynamic response curve under system fault
[1] 王武.鼠笼式感应风力发电系统的优化控制[J].实验室研究与探索,2013 (4):75-78.
[2] 王聪,刘永前.风力发电系统的建模与仿真研究[J].中国电力教育:上,2006 (S1).
[3] 张慧玲,郝思鹏,袁越,等.基于实测数据的双馈风电机组外特性研究及简化建模[J].电力系统保护与控制, 2013,41(17): 82-87.
[4] 龙云,王建全.基于粒子群游算法的同步发电机参数辨识[J].大电机技术,2003 (1): 8-11.
[5] 金宇清,赵泽,鞠平,等.双馈感应风力发电机的参数辨识分析[J].高电压技术,2011, 37(7): 1700-1705.
[6] 赵洋,韦莉,张逸成,等.基于粒子群优化的超级电容器模型结构与参数辨识[J].中国电机工程学报,2012, 32(15): 155-161.
