基于蜂窝结构的二维磁感应通信

刘锋，张志军，张晓彤，徐金梧

（1. 北京信息科技大学 光电信息与仪器北京市工程研究中心 光电测试技术北京市重点实验室，北京100192；2. 俄勒冈医科大学 生物医学学院，俄勒冈 比弗顿 97006；3. 北京科技大学 计算机与通信工程学院，北京 100083；4. 北京科技大学 机械工程学院，北京100083）

1 引言

地表下无线传感器网络在许多领域正得到广泛应用，如土壤参数测量、水质参数测量、地质灾害预测、地下建筑结构监测及海陆边防监测等。为便于测量或者出于安全考虑，上述应用中的传感器往往埋设于地层、水体及建筑材料内部较深位置。由于较长的传感器引线往往受周围物质内部应力影响出现断裂老化现象，或者由于传感器埋设过深，不便于导线连接，传感器节点的收发装置往往与传感器安装在相同位置，传统无线传感器网络将面临极大挑战。首先，地表下无线信号需要在土壤、岩石、矿物质水、钢筋混凝土等半导电媒质中传播；其次，节点一旦完成安装，难以通过更换电池等方式进行续航，节点寿命受到极大限制。

由于土壤、岩石等半导电媒质对电磁波的损耗随信号频率下降而减小，VLF频段的电磁波将由于极低的信号频率而几乎不衰减。然而VLF信号的发射天线物理尺寸极大，无法在地表下无线传感器节点上安装。在研究超材料过程中，发现电容加载的微线圈间可对谐振频率附近的磁感应电流进行传递，形成磁感应（MI， magneto-inductive）波[1～4]。参与MI波传播的线圈，形成波导效应，称为磁波导。将磁波导技术应用于地表下无线传感器网络，可以通过调整线圈的大小和匝数来增加电感，在可接受的电容值下，将磁波导的谐振频率调节至VLF频段，从而实现VLF信号的地表下传递[5，6]。Syms等人对MI波一维、二维、三维的传播形式进行了理论分析[7]，文献[2]的研究表明在不同结构的磁感应网络间同样会存在波的反射及折射现象。不同结构的磁感应网络，信号传输带宽存在差异，需针对不同应用对网络进行优化设计[4]。磁感应波也是目前实现无线能量传输的重要方式[8～11]。NARUSUE等人为提高无线能量传输效率，提出六边形能量传递结构[12]，但未对六边形网络磁感应波的传播特性进行研究。

现有二维磁感应网络多为方形栅格结构。由于方形栅格结构中，能量主要沿栅格的对角方向传播，无法实现网状互联，限制了在地下无线传感器网络中的应用。为实现磁感应波的全向传播，本文提出一种新型的二维蜂窝网络结构，并对系统性能进行理论分析和仿真验证。结果表明，在相同节点密度下，蜂窝结构网络在各传播方向具有更均衡的带宽、群速等，可有效实现磁感应波的全向传播。

2 蜂窝结构磁感应网络系统模型

为研究适用于地表下无线传感器网络的磁感应通信，首先针对传统方形栅格拓扑结构进行了磁感应波近场传播研究，网络拓扑如图 1所示。结果表明，在方形栅格二维网络中，点源激发的磁感应波将只沿栅格对角线方向传播，呈现一维特征，无法形成网状连接，限制了网络的连通度。

图1 方形栅格磁感应网络

为实现二维磁感应网络的网状互联，本文提出一种蜂窝结构二维磁感应网络，拓扑结构如图2所示。网络由电容加载的圆形线圈组成，线圈按照相同间距排列成蜂窝状。每个线圈被其他6个邻居线圈包围。

线圈（n，m）位于第n排第m列，其电流可表示为Im，n，线圈坐标（x，y）可由式(1)给出。

其中，m与n同为奇数或者同为偶数。

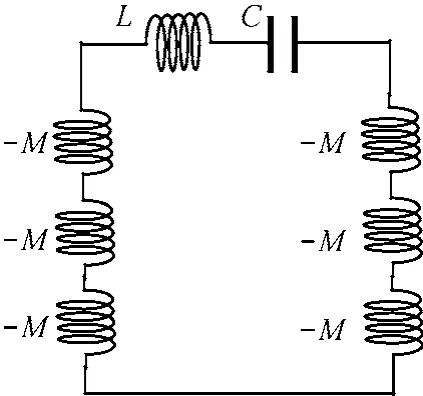
图3 单只线圈等效电原理

对于无耗情况，且只考虑邻近线圈间的耦合效应[13]，线圈的等效电路模型可由图3给出。由于线圈共面放置时，线圈电流将在邻居线圈中产生与自身磁通方向相反的磁场，因此线圈间的互感为负，记为-M。

3 蜂窝结构磁感应网络系统性能分析

3.1 色散方程、带宽及群速

蜂窝结构磁感应网络中各线圈电流间的关系可按基尔霍夫电压定律由式(2)给出。

可以证明，单位面积内具有相同线圈数目时，蜂窝结构网络的线圈间距是方形栅格结构的1.074 6倍。蜂窝结构的耦合系数因此成为方形栅格的 1 .074 6-3倍。式(6)可重写为

比较式(5)与式(7)可知，相同节点密度下，蜂窝网络具有高于方形栅格网络的通带宽度。然而式(5)与式(7)中，只是表示出可传播的最大信号频率与最小频率，并不意味着在某一方向可同时实现最高频率与最低频率信号的传播。需要对各传播方向分别统计频率范围，即信号带宽。

考虑20匝、半径0.1 m的电容加载线圈，谐振频率为10 kHz，分别对线圈间距1 m的方形栅格网络Nlattice与线圈间距1.074 6 m的蜂窝网络Nhoneycomb计算各方向相对带宽ω/ω0，结果如图 4所示。图中角度坐标为磁感应波传播方向。相对于方形栅格，蜂窝网络在各个方向具有更均一的带宽。

图4 2种网络在各传播方向上的带宽

考虑具有单一频率0ω的正弦信号，由式(4)可得

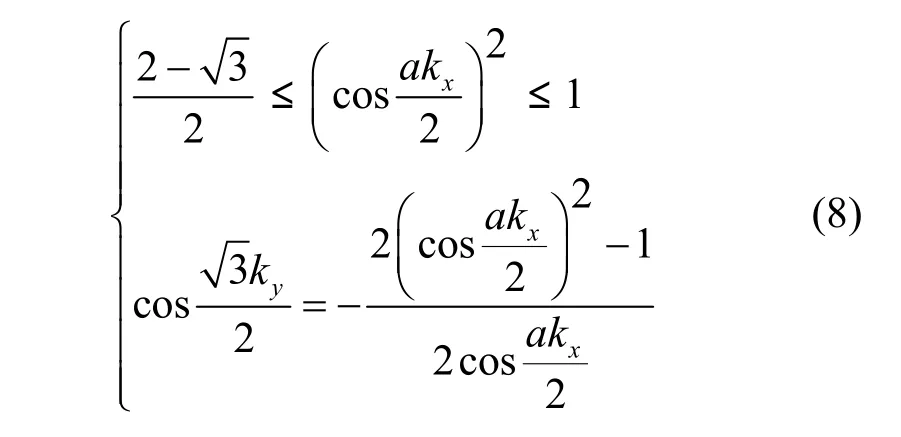
式(8)表明，对于每一对满足式(8)的kx和ky，蜂窝网络均存在一个可传播的磁感应波模式，传播常数为考虑传播常数的物理意义，必小于π/2。图 5给出了上述蜂窝网络中各方向传播平面波的相速。

图5 2种网络在各传播方向的相速

蜂窝磁感应网络的能量流向，为

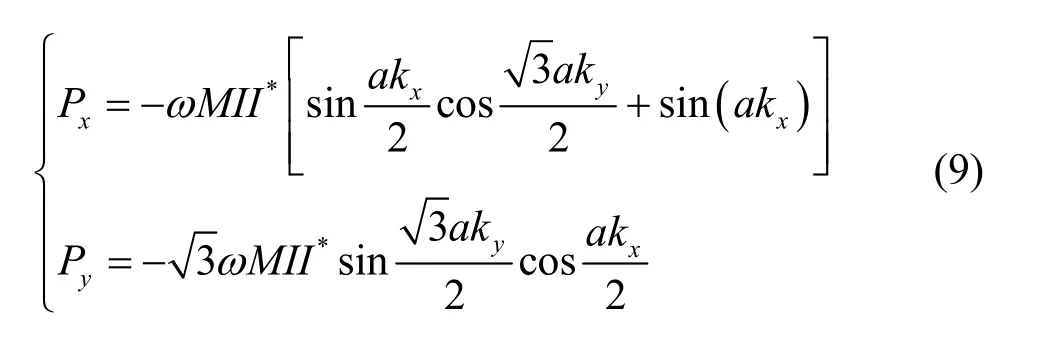
其中，I为线圈中的电流。

在谐振频率为 10 kHz的蜂窝磁感应网络中，各方向能量传播矢量如图 6所示，能量传播方向与相位传播方向基本一致，因此蜂窝磁感应网络中点源激发的磁感应波，不再像方形栅格网络那样，出现一维传播特征，而以二维方式进行传播。

图6 蜂窝网络能量传播矢量

群速度的推导也可得到类似结论。蜂窝磁感应网络中的群速度可由式(10)给出。

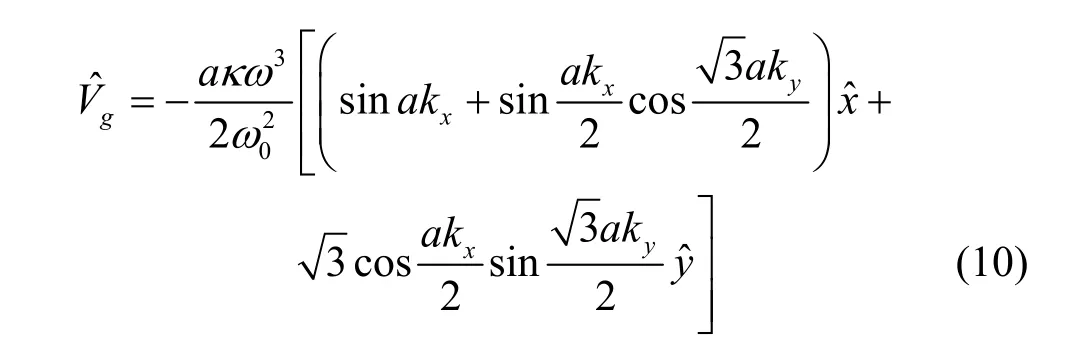
网络Nlattice与Nhoneycomb在各传播方向上的群速如图7所示。

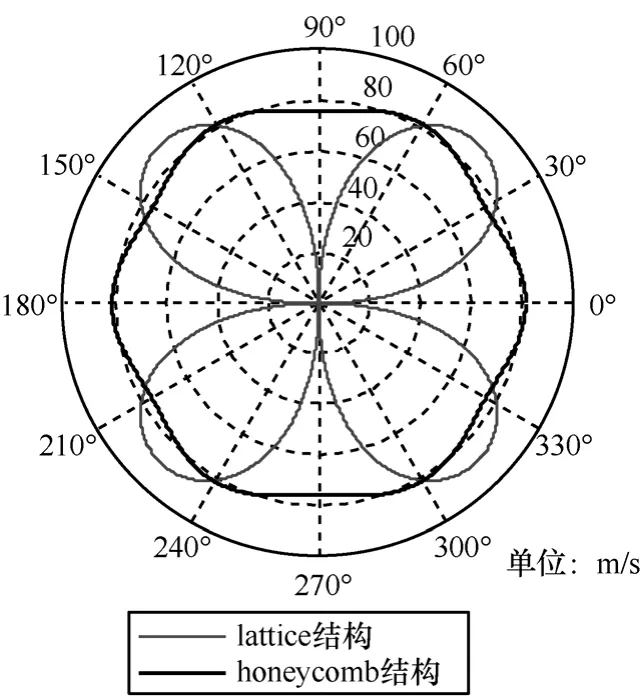
图7 2种网络在各传播方向的群速

3.2 波束成形

蜂窝网络中的磁感应波为准全向波，通过发射端多节点天线协作，在保证线圈间严格时间同步的前提下，调整各天线相位，向特定方向传输信号能量，从而实现磁感应波的波束成形。图8为多天线协作示意图，图中7个线圈协同发射信号。当信号观测点的位置距离发射线圈较远时，观测点与每个线圈之间的夹角差异可以忽略不计，夹角均为α。而观测点与每个发射线圈之间的距离不同，引起接收信号间的相位差异。

图8 蜂窝网络多天线协作示意

调整线圈激励信号的相位，使每个线圈的磁感应波在到达观测点时具有相同相位，天线阵将会在α角度上获得最大信号增益。图9给出了α=225°时，磁感应天线阵的方向图。

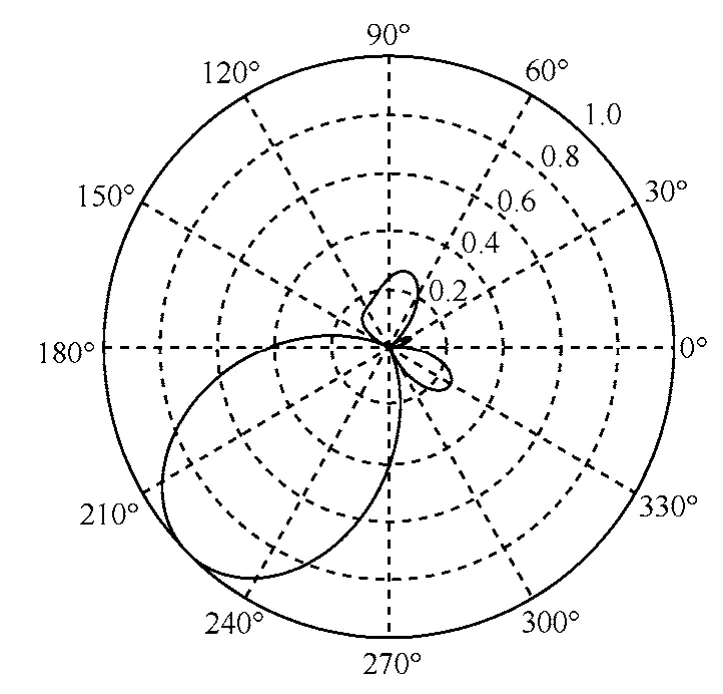
图9 蜂窝网络天线阵225°最大增益方向

4 时域数值仿真

图10为t=0.7 s时，阵列中各个线圈电流分布的仿真结果，横纵坐标分别表示各个磁感应线圈在天线阵列中的行列坐标。由图 10可以看出，中心线圈加载的窄带波包可沿各传播方向向外传播，与图7所示的群速结论一致，即蜂窝磁感应网络可实现磁感应波的二维全向辐射。

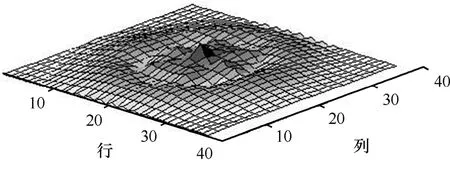
图10 蜂窝磁感应网络的传播仿真

另外，对多线圈协作发射窄带波包信号的情况进行了仿真。当7个协作线圈的相位分别为0， 1.7，2.322， 0.622 2， -1.7， -2.322， -0.622 2 时，将会在225°方向上产生最大信号强度。仿真结果如图 11所示，图中灰度值越高（越亮）表明电流幅度越高。比较图9与图11可知，波束成形的仿真结果与理论计算结果一致。

图11 波束成形仿真

5 结束语

对于方形栅格二维磁感应网络，当某个线圈获得激励时，磁感应波将沿栅格对角方向以一维形式传播，只在对角方向上各节点间建立通信，无法满足无线传感器网络高连通度的需求。

理论分析及仿真实验表明，蜂窝磁感应网络可实现磁感应波的二维全向辐射。在相同节点密度下，蜂窝网络节点间距略有增加，线圈间耦合系数κ降为方形栅格结构的1/1.24，对比2种网络各传播方向的带宽和群速，方形栅格网络仅在4个对角方向上性能略优，而在其他各方向性能均劣于蜂窝结构。同时，可利用蜂窝网络结构的全向传播特性，通过波束成形算法，实现能量和信号的定向辐射，极大提高了能量及信道的利用率。理论与仿真均表明，本文提出的蜂窝磁感应网络结构可满足地下无线传感器网络信号及能量的传播需求，具有较高的理论及实用价值。

[1] WILTSHIRE M C K， PENDRY J B， YOUNG I R，et al. Microstructured magnetic materials for RF flux guides in magnetic resonance imaging[J]. Science， 2001， 291(5505)： 849-851.

[2] SYMS R R A， SHAMONINA E， SOLYMAR L. Positive and negative refraction of magnetoinductive waves in two dimensions[J]. The European Physical Journal B-Condensed Matter and Complex Systems，2005， 46(2)： 301-308.

[3] ELEFTHERIOU M， LAZARIDES N， TSIRONIS G P，et al. Surface magneto-inductive breathers in two-dimensional magnetic metamaterials[J]. Physical Review E， 2009， 80(1)： 017601.

[4] CHAN C W T， STEVENS C J. Two-dimensional magneto-inductive wave data structures[A]. Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP)[C]. 2011.1071-1075.

[5] JACK N， SHENAI K. Magnetic induction IC for wireless communication in RF-impenetrable media[A]. Microelectronics and Electron Devices， WMED 2007[C]. 2007.47-48.

[6] ZHI S， AKYILDIZ I F. Magnetic induction communications for wireless underground sensor networks[J]. IEEE Transactions on Antennas and Propagation， 2010， 58(7)： 2426-2435.

[7] SHAMONINA E， KALININ V A， RINGHOFER K H，et al. Magnetoinductive waves in one， two， and three dimensions[J]. Journal of Applied Physics， 2002， 92(10)： 6252-6261.

[8] NARUSUE Y， KAWAHARA Y， ASAMI T. Impedance matching method for any-hop straight wireless power transmission using magnetic resonance[A]. Radio and Wireless Symposium (RWS)[C]. 2013. 193-195.

[9] KURS A， KARALIS A， MOFFATT R，et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science， 2007， 317(5834)：83-86.

[10] ZHANG F， HACKWORTH S A， FU W，et al. The relay effect on wireless power transfer using witricity[A]. Electromagnetic Field Computation (CEFC)， 2010 14th Biennial IEEE Conference[C]. IEEE，2010.

[11] KAWAHARA Y， WEI W， NARUSUE Y，et al. Virtualizing power cords by wireless power transmission and energy harvesting[A]. Radio and Wireless Symposium(RWS)[C]. 2013.37-39.

[12] NARUSUE Y， KAWAHARA Y， KOBAYASHI N，et al. Position-free parameter determination method for 2D wireless power transmission using magnetic resonance[A]. IEICE Society Conference[C]. 2012.

[13] ELEFTHERIOU M， LAZARIDES N， TSIRONIS G P. Magneto inductive breathers in metamaterials[J]. Physical Review E， 2008， 77(3)：036608.

[14] SYMS R R A， SHAMONINA E， SOLYMAR L. Magneto-inductive waveguide devices[J]. IEEE Proceedings-Microwaves， Antennas and Propagation， 2006， 153(2)： 111-121.