琼东南盆地坡折带斜井时深关系研究

刘兵 周家雄 任科英 刘爱群

中海石油（中国）有限公司湛江分公司

地震解释通常是在时间域开展的，而测井解释则是在深度域开展的，两者通过时深转换来建立地质联系［1－2］，进而开展构造解释、储层描述和油气藏描述等工作。用于时深转换的速度数据来源通常有4种：VSP测井速度、声波测井速度、标志层时间—深度对和地震偏移速度。各种数据的基本原理不同，获取方式不同，精度也存在着很大的差异［3－5］。前人对声波测井和VSP测井的原理以及主要误差影响因素的综合分析结果表明，VSP测井求取的地层平均速度比声波测井更准确，更适合于井震标定和后续时深转换工作［6－7］。标志层时深对通常样点少，精度局限于标志层附近。地震偏移速度以最佳偏移成像为目的，从地震资料间接得到速度信息，与时深转换速度不完全相同［8］。通常需要利用钻井的时深数据、钻井地质分层数据、地震解释时间层位等信息对地震偏移速度进行约束标定，才能建立较准确的速度模型，进而用于时深转换工作［9－11］。多数情况下，以VSP速度、声波测井速度和标志层时深对为基础，通过合成记录标定的方法都可以得到井点位置上准确的时深关系，在实际生产中已被广泛采用。

琼东南盆地坡折带附近中新统梅山组地层发育了一系列坡控重力流海底扇岩性圈闭，是岩性油气藏勘探的重要领域。坡折带伴随着急剧的水深变化，水深由200m到2 000m不等。坡折带在导致地震波场复杂化，地震资料成像、构造归位困难的同时［12］，还给钻后时深关系研究带来了新的难题。为此，笔者分析了斜井变水深条件下，VSP测井和声波测井计算的时深关系与准确时深关系之间的差异，提出通过VSP速度模型正演，准确求取坡折带上的斜井时深关系方法，并将所建模型计算的时深关系与常规方法计算的结果进行了对比。

1 变水深斜井时深关系理论分析

在坡折带上沿斜井轨迹水深变化条件下，必须考虑水深变化给时深关系带来的影响。图1是沿斜井轨迹水深变化条件下，平台震源VSP时深关系与准确时深关系的计算示意图。假设地层由一系列水平各向同性介质组成，地层厚度和速度依次为Hi、vi（i＝1，…，n），上覆水体厚度横向变化为 Hw，速度vw为1 500 m／s，井口位置水体厚度为H0，斜井轨迹依次穿过各地层。在地震尺度内，斜井水平位移范围内地层速度横向变化不大的假设通常是成立的。根据VSP初至时间反演层速度的原理［13－15］可知，VSP计算时深关系的深度和时间数据是沿井轨迹地层厚度和传播时间的累加求和，深度数据为Hi＋H0，时间数据为Hi／vi＋H0／1 500。时间和深度数据采样间隔与VSP测井的观察系统有关。这时，斜井平台震源VSP计算的时深关系与直井类似，对应的水体厚度只有1个，即井口位置上的水体厚度。

当坡折带上沿斜井轨迹水深变化时，要获得准确的时深关系就要求井轨迹上每个深度点对应的时间应该是该点到海平面的垂向传播时间。这个垂向传播时间包括两部分：在厚度不断变化的水体中传播时间和在沉积地层中的传播时间。这与平台震源VSP计算的时深关系具有很大的不同。平台震源VSP计算时深关系无法体现沿井轨迹的水深变化，与准确时深关系会存在很大的误差。声波测井计算的时深关系与平台震源VSP相似，两者只有采样率方面的差异。因此，直接应用VSP数据或声波测井数据进行时深转换时，便会出现很大的误差。

2 变水深斜井VSP速度建模

以实际观测VSP记录为基础，采用VSP速度建模正演模拟的方法，能够获取沿斜井轨迹上不同水深条件下的准确时深关系（图2）。首先，利用叠前深度偏移地震解释剖面，建立深度域过井二维层速度模型（图3－a），井轨迹显示在速度剖面上，不同地层的层速度由声波测井速度得到。其次，利用射线追踪方法开展已钻井的VSP正演模拟，正演VSP记录如图3－b所示。通过初至自动拾取与手工拾取相结合的方法得到正演VSP记录的初至时间，在图3－b中用蓝色的圆圈标注。同时将实际测量的VSP记录初至时间也显示在相同的剖面中，在图3－b中用红色的“＋”号标注。分析正演模拟初至时间和实际测量初至时间的相关关系，对速度模型进行迭代更新。当基于速度模型的正演模拟初至时间和实际测量初至时间高度吻合时，表明二维深度域速度模型是准确的。构建该模型一方面为后续的VSP克希霍夫偏移做好资料准备，同时也给该井的准确时深关系研究提供了基础数据。最后将深度域层速度剖面转换为时间域平均速度剖面，沿井轨迹提取每个深度点的平均速度，并计算各深度点对应的时间，从而获得沿斜井轨迹上不同水深条件下的准确时深关系。

图2 变水深斜井VSP速度建模框图

3 应用实例

A井位于琼东南盆地坡折带上，是针对重力流海底扇岩性圈闭钻探的斜井，沿井轨迹方向水深逐渐增大。井口位置上水深100m，井底位置上水深263m，最大水平位移约1 200m（图4）。钻后开展了声波测井和平台震源VSP测井，并分别应用不同方法计算了该井的时深关系（图5）。图5表明VSP资料和声波测井计算的时深关系类似，基于标志层方法和VSP速度模型计算的时深关系类似。图5中对基于标志层方法和VSP速度建模方法计算时深关系的放大显示可以清楚地看到，在储层段垂深3 000m以下，两种时深关系基本重合，在储层段上方的泥岩段，两者仍存在较大的差异。而图6表明，笔者所建立的VSP速度模型保证了每个深度段上速度的合理性。

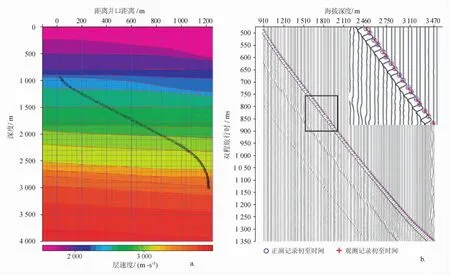
图3 变水深斜井VSP速度建模（a）和正演模拟记录（b）

在浅层直井段上，地层反射特征清晰，合成记录标定多解性少，不同方法计算的时深关系类似。随着深度增加，上新统莺歌海组、中新统黄流组和梅山组一段地层以泥岩为主，夹薄层泥质粉砂岩，地震反射特征以弱—中等强度的连续反射为主，缺少明显的标志层，合成记录标定出现多解性，不同方法计算的时深关系差异变大。由于没有考虑沿井轨迹方向上水深的变化，VSP和声波测井计算的时深关系明显偏离基于标志层方法和VSP速度模型计算的时深关系，平均速度偏大。实践证明，通过VSP资料开展合成记录标定时，需要进行大尺度的时深关系拉伸，地层埋深介于1 500～3 000m范围内的时间校正量超过150ms。

图4 坡折带上沿A井井斜轨迹的典型地震剖面图

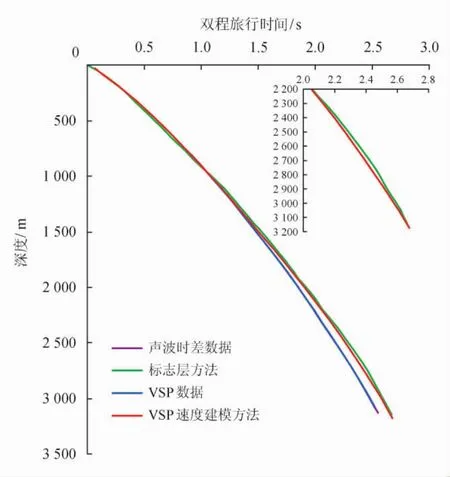
图5 不同方法计算的A井时深关系对比图

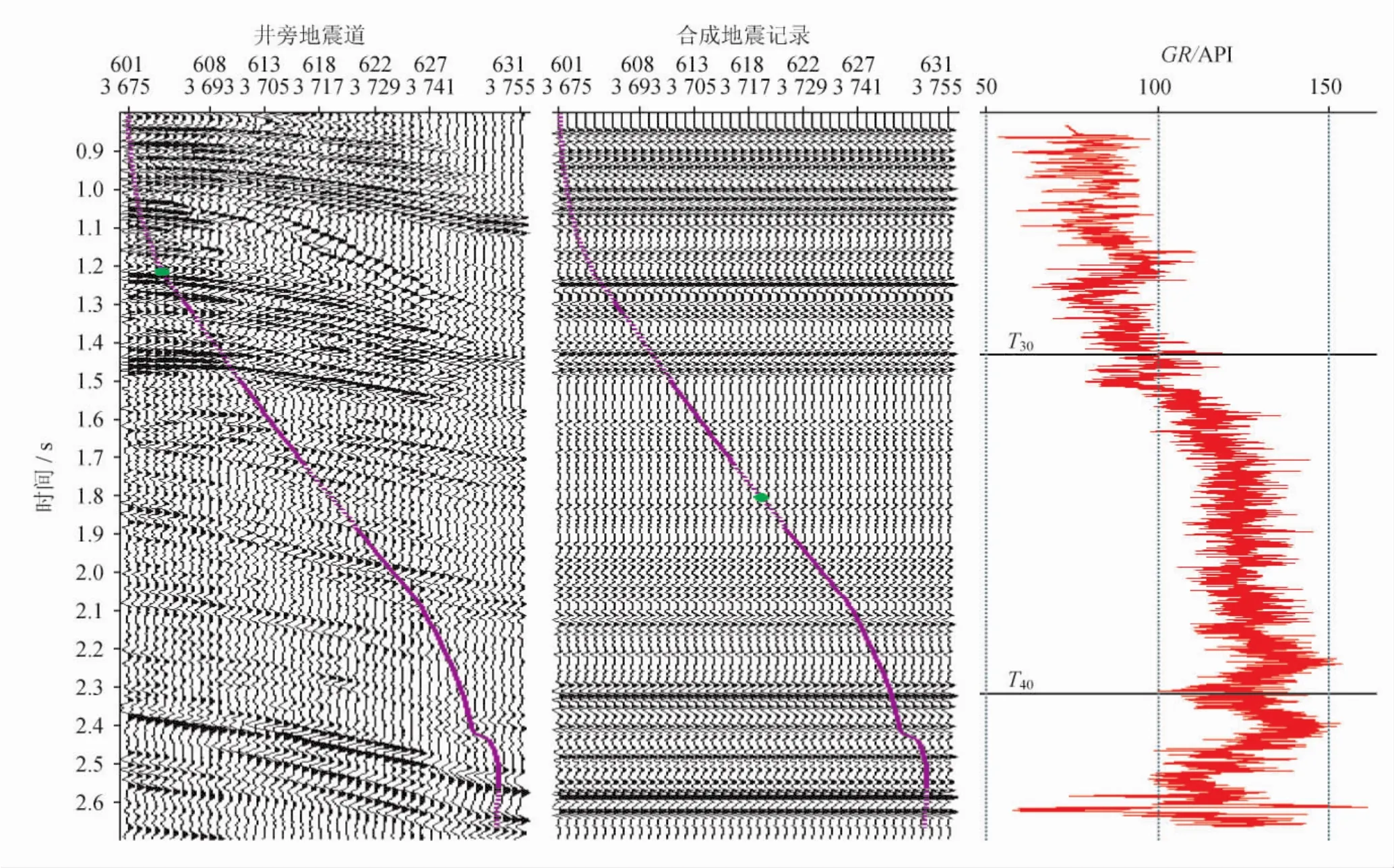
图6 A井合成记录标定剖面图

在莺歌海组、黄流组、梅山组一段以泥岩沉积为主的地层中，由于没有明显的地层反射特征，基于标志层方法计算的时深关系仍然存在多解性。笔者建立的VSP速度模型以VSP初至时间正演模拟为基础，保证了每个深度段上速度的合理性。因此，对反射特征不清楚的地层同样可以保证时深关系的准确性，合成记录标定更加合理（图6）。

4 结论

1）在琼东南盆地坡折带位置上，沿斜井轨迹的水深变化大，常规声波测井和VSP测井计算的时深关系与准确时深关系存在着很大的差异。常规声波测井和VSP测井是沿井轨迹方向计算时间和深度值的，只考虑了井口位置上的水深影响。斜井变水深条件下，时深关系需要计算井轨迹上每个点的垂向深度和对应的传播时间，且不同位置对应着不同的水深值。

2）以VSP测井、声波测井和地震资料为基础，建立斜井附近地层的二维速度模型，开展射线追踪正演模拟。通过分析VSP正演记录初至时间和实测记录初至时间的相关关系，进行速度模型迭代更新，得到最佳速度模型，从而得到坡折带上沿斜井轨迹水深变化条件下的准确时深关系。

3）对比常规基于标志层计算时深关系的方法，所建立的VSP速度建模方法不受地震资料品质的限制，可以保证井轨迹上每个点时深关系的准确性，精度更高。

［1］勒玲，苏桂芝，刘桂兰，等.合成地震记录制作的影响因素及对策［J］.石油物探，2004，43（3）：267－271.LE Ling，SU Guizhi，LIU Guilan，et al.Influencing factors in making synthetic seismogram and counter measures［J］.Geophysical Prospecting for Petroleum，2004，43（3）：267－271.

［2］JONES I F.Tutorial：Time conversion of depth migrated data［J］.First Break，2009，27（7）：51－55.

［3］曹统仁.VSP平均速度的应用［J］.西南石油学院学报，1999，21（2）：54－56.CAO Tongren.Application of VSP average velocity［J］.Journal of Southwest Petroleum Institute，1999，21（2）：54－56.

［4］刘海河.准确求取VSP时间—深度关系的探讨［J］.测井技术，2004，28（4）：289－291.LIU Haihe.On accurately acquiring time－depth relationship using VSP data［J］.Well Logging Technology，2004，28（4）：289－291.

［5］张蓉，徐群洲，帕尔哈提，等.对提高地层压力预测精度的探讨——声波测井层速度与地震层速度的关系［J］.石油天然气学报，2010，32（2）：274－276.ZHANG Rong，XU Qunzhou，PA Erhadi，et al.Discussion of improving the accuracy of layer pressure predictionthe relationship of interval velocity between sonic logging and seismic data［J］.Journal of Oil and Gas Technology，2010，32（2）：274－276.

［6］曾照荣，肖玲，白兴盈，等.声波测井与VSP测井平均速度的对比分析［J］.新疆石油地质，2004，25（1）：50－52.ZENG Zhaorong，XIAO Ling，BAI Xingying，et al.Correlation of mean velocities between sonic logging and VSP logging［J］.Xinjiang Petroleum Geology，2004，25（1）：50－52.

［7］郭超，焦健.声速测井与VSP速度对比研究［J］.西安文理学院学报：自然科学版，2011，14（2）：86－88.GUO Chao，JIAO Jian.A comparative study of acoustic log and VSP［J］.Journal of Xi＇an University of Arts and Science：Natural Science Edition，2011，14（2）：86－88.

［8］AI CHALABIM.Seismic velocities－a critique［J］.First Break，1994，12（12）：589－596.

［9］CAMERON M，FOMEL S，SETHIAN J.Time－to－depth conversion and seismic velocity estimation using time－migration velocity［J］.Geophysics，2008，73（5）：205－210.

［10］王香文.东岭地区三维速度模型的建立和应用［J］.勘探地球物理进展，2006，29（6）：412－414.WANG Xiangwen.3－D velocity model building and its application in Dongling area［J］.Progress in Exploration Geophysics，2006，29（6）：412－414.

［11］唐必锐，覃发兰，黄花香，等.四川东部高陡构造时深转换方法研究［J］.天然气工业，2005，25（8）：41－43.TANG Birui，QIN Falan，HUANG Huaxiang，et al.Research on time－depth conversion method of the high－steep structures in East Sichuan［J］.Natural Gas Industry，2005，25（8）：41－43.

［12］李列，朱江梅，杨薇，等.海洋坡折带地震资料处理关键技术［J］.地球物理学进展，2013，28（4）：1975－1982.LI Lie，ZHU Jiangmei，YANG Wei，et al.Key technologies in ocean shelf break seismic data processing［J］.Progress in Geophysics，2013，28（4）：1975－1982.

［13］孙赞东.三维三分量VSP方法原理及应用［M］.北京：石油工业出版社，2011.SUN Zandong.The principle and application of 3D3CVSP［M］.Beijing：Petroleum Industry Press，2011.

［14］陈信平.由VSP初至时间反演层速度的算法和误差估计［J］.石油地球物理勘探，1992，27（6）：744－752.CHEN Xinping.Method for interval velocity inversion using VSP first break time and the error estimation［J］.Oil Geophysical Prospecting，1992，27（6）：744－752.

［15］庄东海，肖春燕.VSP资料求层速度的射线追踪折线法［J］.江汉石油学院学报，1994，16（4）：50－53.ZHUANG Donghai，XIAO Chunyan.Refraction line method of calculating interval velocity by ray tracing using VSP data［J］.Journal of Jianghan Petroleum Institute，1994，16（4）：50－53.