跨断层区X80钢管道受压时的设计应变预测

刘啸奔 陈严飞 张 宏 夏梦莹 郑 伟 张振永 梁乐才 陈金孝

1.中国石油大学（北京）机械与储运工程学院 2.中国石油天然气管道工程有限公司

活动断层是地震区天然气长输管道的主要威胁，断层作用下管道会发生轴向和垂向位移，导致管道内产生较大的应变而失效。所以断层作用下管道应变的准确计算对断层区管道的设计与安全评估具有重要意义。国内外大量学者针对断层区管道的应力应变分析进行了大量研究［1－12］，提出了多种理论和数值计算方法，其中在工程中应用最广泛的为Newmark－Hall和Kennedy方 法［3－4］，但 是 其 只 能 求 解 管 道 穿 越 角 小于90°时的管道受拉情况，无法求解管道穿越角大于90°时管道的受压情况。

Karamitros等［5］提出并验证了管道在断层作用下产生空间错动时，可简化为一个走滑断层作用和一个管道垂直穿越的正或逆冲断层作用。走滑断层产生与空间断层一致的管道轴向与侧向位移，管道垂直穿越的正或者逆断层产生与空间断层一致的管道轴向与垂向位移。在该假设下，管道以小于90°穿越逆冲断层时，断层在管道轴向产生了压缩位移，简化后走滑断层的穿越角度变为大于90°，现有的解析方法无法求解。而工程实例却表明，管道以这种形式穿越的断层大量存在，如“西气东输二线”穿越西山断裂、王家沟断裂［13］等。

对此，笔者建立了穿越角度大于90°时跨断层区X80钢管应变计算有限元模型，研究了管道直径、壁厚、内压、断层错动量、穿越角和土壤特性5种主要影响参数对管道设计应变（最大压应变）的影响。基于计算得到的超过2 000种工况下管道的设计应变值，拟合得到了穿越角度大于90°时的跨断层区X80钢管设计应变回归公式。并与“西气东输二线”实际工况参数的有限元结果对比验证。所给出的方法可以为断层区X80钢管基于应变的设计与安全评价提供一定的参考。

1 数值模型

1.1 有限元模型

图1为管道以大于90°穿越角度穿越断层时的示意图。断层造成地表错动，产生沿管道轴向和侧向的位移。以管道轴向为x方向，侧向为y方向，建立笛卡尔坐标系。可以将断层错动量δs分解为一个管道轴向分量ΔX和侧向分量ΔY。

图1 管道穿越断层示意图

目前有限元模型中管道主要使用梁单元（BEAM）、管单元（PIPE）、弯管单元（ELBOW）或壳单元（SHELL）来 模 拟［6－9，11－18］。 笔 者 采 用 ABAQUS 非线性有限元软件建立管道跨断层有限元模型，模型使用管单元和弯管单元模拟管道。为消除边界的影响，管道总长取为2 000m，断层两侧各1 000m，模型两端900m管道采用PIPE31单元，单元长度为1m，模型中间200m管道采用ELBOW31单元，单元长度为0.1m。

1.2 管土相互作用

根据 ASCEGuidelinesfortheDesignofBuried SteelPipe［2］，断层作用下，土壤对管道的作用可以用弹塑性土弹簧来表示，包括管道轴向、侧向和垂向的土弹簧（图2）。笔者采用管土相互作用（PSI）单元模拟管土相互作用，PSI单元如图2－b所示，由4个节点组成，单元上端2个节点（3和4）与地表面相连，反映地面运动与位移，下端2个节点（1和2）与管道单元相连，管土相互作用关系以非线性单元刚度表示，单元刚度与土弹簧刚度一致。通过将断层位移施加在断层右侧PSI单元的土壤节点上可以来模拟断层的作用。等效土弹簧的力学性能可以用极限抗力与屈服位移2个量来描述。Pu、Tu、Qu和Qd代表了3个方向的极限抗力，Δp、Δt、Δqd和Δqu代表了3个方向的屈服位移（图3）。

1.3 管材模型

采用Ramberg－Osgood模型来描述管材的弹塑性特征，表达式如下：

图2 管土相互作用示意图

图3 土弹簧的非线性模型示意图

式中E为管材的初始弹性模量；ε为应变；σ为应力；σS为管材的屈服应力；α和N为R－O模型参数。对X80钢管材拉伸实验结果的真实应力应变曲线下限值进行拟合［10］，得到参数取值如下：E＝206 000MPa；σs＝552MPa；α＝0.86；N＝28。管道真实应力应变关系如图4所示。

1.4 计算参数取值范围

根据“西气东输二线”工程管道的实际运行参数与沿途断层参数，对模型计算参数进行取值，得到的模型计算参数范围如表1所示。这里需要说明的是，直接研究断层对管道在空间中造成的错动虽然更加符合实际，但该情况下影响参数众多，很难得到设计应变与各影响参数间的准确关系与回归公式。所以笔者只讨论管道错动分解后位于水平面内的情况。当分析管道在水平面内错动时，垂直向上与向下的土弹簧对管道的应变不再产生任何影响，所以可以不用考虑。而管道的轴向土弹簧与侧向土弹簧的取值范围由“西气东输二线”中出现的管道埋深、回填土和场地土性质参考ASCEGuidelinesfortheDesignofBuriedSteel Pipe方法进行计算确定。可以得到各参数取值范围如表1所示。

图4 X80管道应力应变曲线图

表1 X80钢管穿越断层区计算参数取值范围表

2 参数分析

采用上述非线性有限元模型，对表1所列参数下工况进行计算，在对表1中数据进行计算时，采用因素轮换法分析各个参数对设计应变的影响，考虑参数之间的相互影响。为了准确得到设计应变与各参数之间变化关系，对超过2 000组工况进行了计算。

图5 不同穿越角度下设计应变与断层位移的关系图

2.1 断层位移与穿越角的影响

图5为不同穿越角度下设计应变与断层位移的关系图，图5表明，管道的设计应变在所有大于90°的穿越角度下都随着断层位移的增大而增大。随着断层位移的加大，设计应变增大速度变快。当穿越角度小于135°时，角度越大设计应变越大，设计应变随断层位移的变化速度越快；当穿越角度大于135°时，角度越大设计应变越小，设计应变随断层位移的变化速度越慢。可以得到，在所有穿越角度下，设计应变与断层位移均表现为近似幂函数关系。

为了更深入分析设计应变与穿越角度的关系，图6给出了不同断层位移下设计应变随穿越角度的变化关系。从图6可以看出，当断层位移量小于0.8m时，设计应变较小，变化也较小；当断层位移量大于0.8m时，设计应变随着穿越角度的增大先增大后减小，在所有断层位移下，设计应变与穿越角度之间存在着相似的函数关系，可以用二次多项式来描述。

图6 不同断层位移下设计应变与穿越角的关系图

2.2 管径与壁厚的影响

图7、8给出了不同断层错动位移下管径和壁厚对设计应变的影响。从图7－a和图8－a可以看出，管径和壁厚越大，设计应变越小，但在不同的管径和壁厚下设计应变和断层错动量都保持着相似的函数关系。图7－b和图8－b给出了不同断层位移下设计应变与管径和壁厚的变化规律，可以看出，设计应变随管径和壁厚的变化规律比较一致，也可以用幂函数来描述。

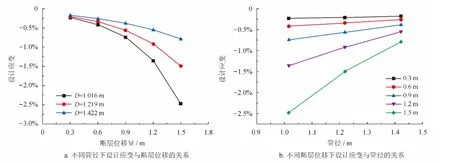
图7 断层位移量与管径对设计应变的影响图

图8 断层位移量与壁厚对设计应变的影响图

2.3 内压的影响

考虑0MPa、4MPa、8MPa、12MPa这4种不同内压工况下设计应变的变化规律。由有限元结果可以得到，设计应变在不同内压下随断层位移的变化规律比较类似（图9）。为了进一步分析内压对设计应变的影响，分析了不同断层位移下设计应变随内压的变化情况。从图9－b可以看出，当断层位移量大于1m时，设计应变在4MPa时应变最小；当断层位移量小于1 m时，设计应变较小，不同内压下设计应变的差距变得不大明显。

2.4 土壤特性的影响

通过研究不同土弹簧的取值影响来考虑土壤特性对管道设计应变的影响，图10给出了不同轴向和侧向土弹簧下设计应变的变化规律。由图10－a可以得到，轴向土弹簧越大，设计应变越大。在不同轴向土弹簧下管道设计应变随断层位移量的变化形式保持一致，依旧保持着类似幂函数的关系。这里分析不同侧向土弹簧下应变随轴向土弹簧的变化规律来分析轴向和侧向土弹簧的相互影响，从图10－b可以发现，在不同侧向土弹簧下设计应变随轴向土弹簧保持单调的规律，轴向土弹簧越大设计应变越大，同时侧向土弹簧越大设计应变也越大。

使用同样的方法分析侧向土弹簧对设计应变的影响（图11）。对比图11和图10，可以得到设计应变随侧向土弹簧的变化形式与轴向土弹簧类似。从图11－a可以发现，侧向土弹簧越大，设计应变越大，设计应变在不同侧向土弹簧下与断层位移量均保持类似幂函数关系；从图11－b可以发现，设计应变随侧向土弹簧也保持着类似幂函数的关系。

图9 断层位移量与内压对设计应变的影响图

图10 断层位移量与轴向土弹簧对设计应变的影响图

图11 断层位移量与侧向土弹簧对设计应变的影响图

3 设计应变计算公式回归

基于有限元分析结果，给出了穿越角度大于90°时跨断层区X80钢管设计应变的回归公式。根据参数分析得到的各参数对设计应变的影响规律可以得到设计应变的回归公式形式如下：

式中D为管道直径，m；t为管道壁厚，m；δs为断层位移，m；β为管道穿越角，（°）；p为管道内压，MPa；Tu为轴向土弹簧大小，kN／m；Pu为侧向土弹簧大小，kN／m；k和μ 为无量纲化参数，k＝1m－1，μ＝0.01 m／kN；a1～a13是待定系数。

基于超过2 000组设计应变数据，采用MATLAB非线性拟合工具箱求解得到待定系数值如下：

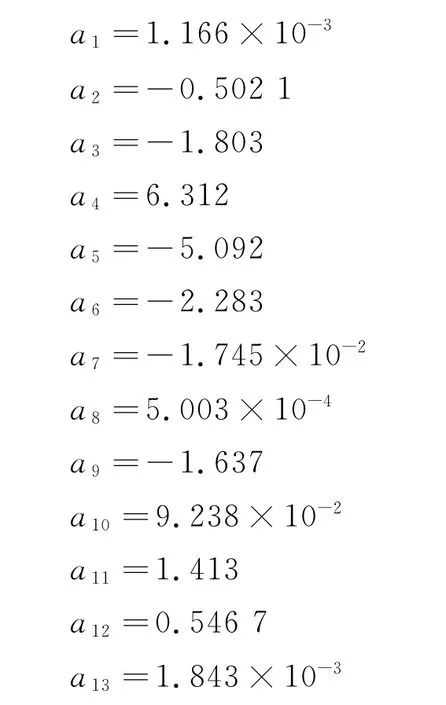
为了验证公式的准确性，本使用“西气东输二线”工程中30种工况参数的应变计算结果进行对比分析（图12），从图12中可以发现本文给出的回归公式精度较高，可以对穿越角度大于90°时跨断层区X80钢管的设计应变进行预测。

4 结论

基于非线性有限元分析，给出了穿越角度大于90°时跨断层区X80钢管设计应变计算方法，讨论了管径、壁厚、断层位移量、穿越角度、土壤特性5种主要参数对设计应变的影响。基于数值计算结果，回归得到了穿越角度大于90°时跨断层区X80钢管设计应变的计算公式。通过与“西气东输二线”工程中实际案例对比验证了回归公式的准确性。给出的断层区X80钢管设计应变计算公式可以为管道的设计与安全评估提供一定的参考。

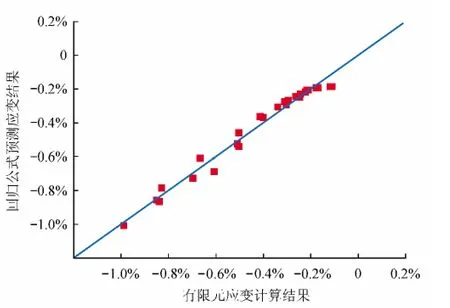
图12 回归公式预测结果与实际工况参数有限元结果对比图

［1］马正茂，冯启民，徐志诚，等.SY／T 0450—2004输油（气）埋地钢制管道抗震设计规范［S］.北京：石油工业出版社，2004.MA Zhengmao，FENG Qimin，XU Zhicheng，et al.SY／T 0450－2004Code for seismic design of oil and gas steel pipeline［S］.Beijing：Petroleum Industry Press，2004.

［2］American Lifelines Alliance－ASCE.Guidelines for the design of buried steel pipe（with addenda through February 2005）［S］.New York：American Society of Civil Engineers，2005.

［3］NEWMARK N M，HALL W J.Pipeline design to resist large fault displacement［C］∥proceedings of the U.S.National Conference on Earthquake Engineering，16－25April 1975，Ann Arbor，Michigan，USA.Michigan：University of Michigan，1975.

［4］KENNEDY R P，DARROW A W，WILLIAMSON R A.Fault movement effects on buried oil pipeline［J］.Transport Engineering Journal，1977，103（5）：617－633.

［5］KARAMITROS D，BOUCKOVALAS G，KOURETZIS G，et al.An analytical method for strength verification of buried steel pipelines at normal fault crossings［J］.Soil Dynamics and Earthquake Engineering，2011，31（11）：1452－1464.

［6］KARAMITROS D，BOUCKOVALAS G，KOURETZIS G.Stress analysis of buried steel pipelines at strike－slip fault crossings［J］.Soil Dynamics and Earthquake Engi－neering，2007，27（3）：200－211.

［7］TRIFONOV O V，CHERNIY V P A.Semi－analytical approach to a nonlinear stress－strain analysis of buried steel pipelines crossing active faults［J］.Soil Dynamics and Earthquake Engineering，2010，30（11）：1298－1308.

［8］刘学杰，孙绍平.地下管道穿越断层的应变设计方法［J］.特种结构，2005，22（2）：81－85.LIU Xuejie，SUN Shaoping.Strain based design of buried pipelines crossing faults［J］.Special Structures，2005，22（2）：81－85.

［9］顾晓婷，张宏，王国丽，等.大口径天然气管道穿越断层的管沟设计研究［J］.天然气工业，2009，29（8）：106－108.GU Xiaoting，ZHANG Hong，WANG Guoli，et al.Trench design for buried cross－fault large－diameter gas pipelines［J］.Natural Gas Industry，2009，29（8）：106－108.

［10］刘冰.基于应变的管道设计准则与方法研究［D］.北京：中国石油大学（北京），2008.LIU Bing.Strain－based design criteria and method of pipeline［D］.Beijing：China University of Petroleum（Beijing），2008.

［11］JOSHI S，PRASHANT A，DEB A，et al.Analysis of buried pipelines subjected to reverse fault motion［J］.Soil Dynamics and Earthquake Engineering，2011，31（7）：930－940.

［12］闫相祯，张立松，杨秀娟.管道穿越地震断层管土耦合大变形壳模型的应变响应规律研究［J］.土木工程学报，2010，43（8）：132－139.YAN Xiangzhen，ZHANG Lisong，YANG Xiujuan.Strain response study of oil gas pipeline crossing earthquake fault based on pipeline－soil coupling and large deformation shell model［J］.China Civil Engineering Journal，2010，43（8）：132－139.

［13］余志峰，王国丽，史航，等.Q／SY GJX 0136—2008西气东输二线管道工程强震区和活动断层区段埋地管道基于应变设计导则［S］.北京：石油工业出版社，2008.YU Zhifeng，WANG Guoli，SHI Hang，et al.Q／SY GJX 0136－2008Guideline for strain－based design in seismic area and active fault crossing of the second west－east natural gas transportation pipeline project［S］.Beijing：Petroleum Industry Press，2008.

［14］朱秀星，仝兴华，薛世峰.跨越断层的埋地管道抗震设计［J］.油气储运，2009，28（10）：30－33.ZHU Xiuxing，TONG Xinghua，XUE Shifeng.Aseismic design for buried pipeline crossing fault［J］.Oil and Gas Storage and Transportation，2009，28（10）：30－33.

［15］姚安林，徐涛龙，郑健，等.河流穿越高压输气管道临界悬空长度的数值模拟研究［J］.工程力学，2013，30（3）：152－158.YAO Anlin，XU Taolong，ZHENG Jian，et al.Study on numerical simulation of critical suspended length of highpressure gas pipelines crossing riverbed［J］.Engineering Mechanics，2013，30（3）：152－158.

［16］张鹏，魏韡，崔立伟，等.地表冲沟条件下悬空管道的力学模型与延寿分析［J］.天然气工业，2014，34（4）：142－148.ZHANG Peng，WEI Wei，CUI Liwei，et al.A mechanical model and life extension analysis of suspended pipelines under the condition of geological gulch［J］.Natural Gas Industry，2014，34（4）：142－148.

［17］吴晓南，卢泓方，黄坤，等.基于频谱分析的地震带输气管道应力分析方法［J］.天然气工业，2014，34（5）：152－157.WU Xiaonan，LU Hongfang，HUANG Kun，et al.Stress analysis of gas pipelines at seismic belts based on the spectrum analysis［J］.Natural Gas Industry，2014，34（5）：152－157.

［18］刘爱文，胡聿贤，赵凤新，等.地震断层作用下埋地管道壳有限元分析的等效边界方法［J］.地震学报，2004，26（增刊1）：141－147.LIU Aiwen，HU Yuxian，ZHAO Fengxin，et al.An equivalent－boundary method for the shell analysis of buried pipelines under fault movement［J］.Acta Seismologica Sinica，2004，26（S1）：141－147.