随机相位编码在多普勒天气雷达中的应用

刘生锋，严 勇，陆建兵

(1.中国兵器工业试验测试研究院， 陕西华阴714200;2.南京电子技术研究所， 南京210039)

0 引言

雷达的最大不模糊距离与雷达的最大不模糊速度是一个矛盾，要增加测速的范围必然要减少测距的范围。当最大不模糊距离外存在目标物时，就会在雷达回波图上出现因距离折叠而形成的二(多)次回波［1］。在多普勒天气雷达中，尤其是对中小尺度强对流天气系统进行观测时，为了避免产生速度模糊，往往需要采用比较高的重复频率，这时远距离回波就会产生折叠、与正常回波混叠在一起，使数据质量大为下降［2-3］。迄今为止，已提出了多种方法解决距离折叠，但各种方法均有不足的地方，最好的方法也只能是减轻它的影响［4］。

在多普勒天气雷达中，常用的退距离折叠方法有:批处理方法［5］、分离扫描法［5］、系统相位法［6］和随机相位法［7］等。本文详细阐述使用相位编码退距离折叠的原理，并将该技术应用于某X波段多普勒天气雷达。实际探测结果表明，使用伪随机相位编码可以有效地解决多普勒天气雷达的距离折叠问题，但也会在一定程度上使真实回波有所减弱，并消去边缘的弱回波。

1 距离折叠的产生机制

1.1 最大不模糊距离

多普勒天气雷达的测距原理与一般雷达的测距原理相同，即它也是通过测量目标物的后向散射波回到雷达时所需的时间来计算目标距离的。因此，多普勒天气雷达的最大不模糊距离可以描述为:当雷达发出一个脉冲遇到该距离处的目标物，产生的后向散射波回到雷达时，下一个雷达脉冲刚好发出。该距离可用下式表示

式中:c为光速;PRF为雷达的重复频率。

由于光速c是一个常数，最大不模糊距离Rmax与脉冲重复频率PRF成反比。

1.2 最大不模糊速度

多普勒天气雷达测量速度时，通常不是直接测量多普勒频移，而是通过测量相继返回的脉冲对之间的相位差来确定目标物的径向速度Vr，见下式

式中:T为脉冲重复周期;ΔR为相继脉冲的时间间隔内T目标物沿径向变化的距离;λ为雷达的波长;Δφ为相继返回的两个脉冲之间的相位差;PRF为雷达的重复频率。

由于多普勒天气雷达的采样是离散的，即每个脉冲采样一次，这就造成了Δφ的取值范围只能在(-π，π)之间。这里，相移π所对应的目标物径向速度值称为最大不模糊速度Vmax，它与脉冲重复频率PRF和波长λ的关系可以通过将π带入式(2)中得到

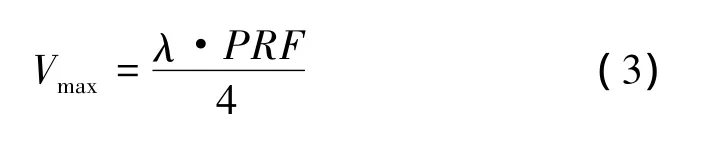
对于给定的雷达，波长λ为一定值，因此最大不模糊速度Vmax与脉冲的重复频率PRF成正比。

1.3 最大不模糊距离与最大不模糊速度之间的关系

将式(1)和式(3)相乘后，可以得到

式(4)就是最大不模糊距离与最大不模糊速度之间的关系。由此可见，当雷达波长选定后，二者的乘积是一个常数，也就是说，最大不模糊距离Rmax与最大不模糊速度Vmax是相互制约的，当增大其中的一个时，必然会导致另外一个减小;而且波长越短，约束条件越苛刻。

1.4 距离折叠

当目标物离雷达的距离大于Rmax且位于kRmax+Rs(k表示任意整数，Rs为小于Rmax的正数)位置处时，在雷达回波上该目标将出现在距离Rs上，这就是“距离折叠”。距离在Rmax内的回波称为一次回波，距离在Rmax和2Rmax内(k=1)的回波称为二次回波，依次类推，甚至可能存在3次(k=2)或更高次(k＞2)的回波。当使用多普勒天气雷达观测中小尺度的强对流天气［8］时，为了减少速度模糊，常选用较高的PRF，这时Rmax就会减小，导致距离折叠。出现距离折叠时，二次或更高次回波将折叠在一次回波中，导致我们对回波出现的位置产生错误判断并影响产品的数据质量，图1给出了一个比较明显的例子。

图1a)为高重频下的强度回波，最大探测距离为75 km;图1b)为较低重频下的强度回波，最大探测距离为150 km。由图1b)可知，在距离雷达75 km范围内几乎没有回波，而在75 km以外，有一片回波;而在图1a)中，75 km范围内却出现了回波，这片回波是虚假回波，是由于距离折叠产生的二次回波，严重影响了回波数据的质量。

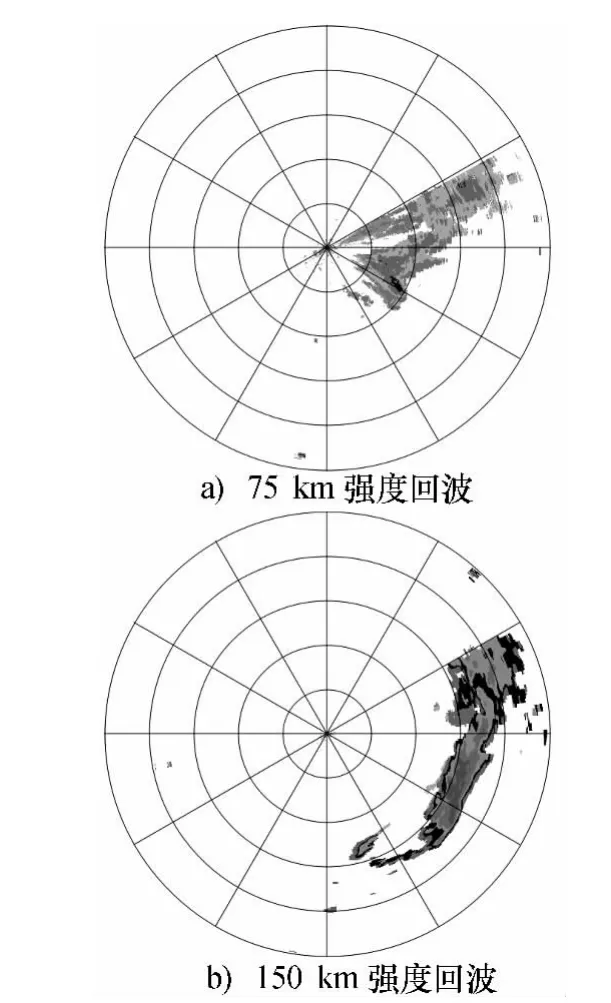
图1 高重频下的距离折叠

2 随机相位编码退距离模糊的原理

随机相位法的基本原理是对不同的脉冲串，在发射之前对其先随机的移一个相角，由于不同距离段所移的相角不同，故能把不同距离段的信号区分开来。当第一距离段和第二距离段都存在气象目标时，第n个发射脉冲的回波信号可表示为

多普勒气象雷达是一个使用速调管发射机的全相参雷达。雷达由接收机产生一个优化的随机相位码去控制发射机的射频移相器，从而使每一个发射脉冲的起始相位都是随机的，该相位相当于式(5)中的φn，当我们将接收回波序列进行相干时，有

式中:［N］表示所有白噪声总功率。

由于φn为(-π，π)均匀分布的随机相位，因此上述两式中的和成了白噪声，从而达到了第一距离段和第二距离段真实回波信号的分离。在上述分离方法中，由于其中一个距离段的白化会导致另一距离段的信噪比下降，特别是对于第二距离段而言，由于第一距离段的回波信号较强，白化后使第二距离段信噪比变得很差。因此，在实际估计时通常采用自适应滤波方法。假设我们要处理第一距离段回波信号，先对第二距离段信号进行相干，恢复其功率谱(由于发射脉冲具有不同的随机初始相位，该回波刚到达接收机时是被白化的)后，构造一个滤波器，将该相干功率滤除，使其成为一白色谱，然后用IFFT反变换后再与第一距离段进行重相干，这样就可以恢复第一距离段信号谱，并且该信号谱的信噪比也得到了改善，接下来再按照FFT方法的各种处理步骤计算雷达回波参数。

3 应用实例

我们对某X型波段多普勒天气雷达中进行了改造，根据随机相位编码退距离模糊的原理，在发射每个脉冲时，由接收机产生一个随机相位码(0，π/2，π，3π/2)去控制发射机的射频移相器，从而使每一个发射脉冲的起始相位都是随机的，在接收时再将不同距离段的回波信号进行分离。图2给出了一次实际探测的结果。

图2 使用随机相位编码退距离模糊的对比

图2a)为量程300 km的强度回波图，在接近300 km、方位210°附近有一片回波(图中的A区)，图2b)为量程150 km、未使用随机相位编码退距离折叠的强度回波图，因此在B区产生了图2a)中A区回波的二次回波，图2c)的量程同样为150 km，但由于使用了随机相位编码，因此在B区没有回波，说明该区域因距离折叠产生的二次回波已经被消去。同时，仔细对比图2三个图中的C区，因为使用了随机相位编码技术，真实回波有所减弱，边缘弱信号更是由于信噪比下降，在低于雷达检测门限后无法检测得到。

4 结束语

距离折叠是多普勒天气雷达中经常会出现的现象，严重影响雷达的数据质量，甚至会导致对天气形势的误判。本文在分析了距离折叠的产生机制后，详细阐述了利用随机相位编码进行退距离模糊的原理，并结合某型X波段多普勒天气雷达对该技术进行了成功的应用。探测结果表明，采用随机相位编码技术可以有效消去由距离折叠而产生的二(多)次回波;但与此同时，也会使真实回波有所减弱，边缘弱信号甚至无法检测到。这是使用随机相位编码退距离折叠需要考虑的问题，也是我们下一步要解决的问题。

［1］ 丁鹭飞，耿富录.雷达原理［M］.西安:西安电子科技大学出版社，2002.Ding Lufei，Geng Fulu.Radar principle［M］.Xi＇an:Xidian University Press，2002.

［2］ 俞小鼎，姚秀萍，熊廷南，等.多普勒天气雷达原理与业务应用［M］.北京:气象出版社，2006.Yu Xiaoding，Yao Xiuping，Xiong Tingnan，et al.Principle and professional application of Doppler weather radar［M］.Beijing:China Meteorological Press，2006.

［3］ 张霭琛.现代气象观测［M］.北京:北京大学出版社，2008.Zhang Aichen.Modern meteorological observation［M］.Beijing:Peking University Press，2008.

［4］ 潘新民，熊 毅，柴秀梅，等.新一代天气雷达退数据模糊方法探讨［J］.气象与环境科学，2010，33(1):17-23.Pan Xinming，Xiong Yi，Chai Xiumei，et al.Discussion on the CINRAD correcting data ambiguity method［J］.Journal of Meteorologyical and Environment Sciences，2010，33(1):17-23.

［5］ 周红平，沙雪松，张光峰.批次处理解决气象雷达距离模糊［J］. 现代雷达，2006，28(11):20-21，32.Zhou Hongping，Sha Xuesong，Zhang Guangfeng.Resolving range ambiguity of weather radar using batch processing method［J］.Modern Radar，2006，28(11):20-21，32.

［6］ Torres S M，Zrnic D S.Range and velocity ambiguity mitigation techniques for the WSR-88D weather radar［C］//2004 IEEE International Geoscience and Remote Sensing Symposium Anchorage，AK:IEEE Press，2004:1727-1729.

［7］ 熊 毅.多普勒天气雷达中相位编码退距离模糊的研究［D］.北京:北京邮电大学，2011.Xiong Yi.Research of phase coding algorithm to mitigate range ambiguity in doppler weather radar［D］.Beijing:Beijing University of Posts and Telecommunications，2001.

［8］ 张培昌，杜秉玉，戴铁丕.雷达气象学［M］.北京:气象出版社，2001.Zhang Peichang，Du Bingyu，Dai Tiepi.Radar meteorology［M］.Beijing:China Meteorological Press，2001.