高风险必备产品制造企业的政府干预研究及对中国的启示——基于美国制药业的分析

赵春江，王 晨

（1．哈尔滨商业大学 财政与公共管理学院，黑龙江 哈尔滨150028；2．德克萨斯A＆M大学 化学工程系，美国 德克萨斯州大学城77843）

一、引 言

药品短缺已经成为长期困扰欧洲及美洲各国的一个主要问题，虽然药品短缺对制造商的影响很小，但对卫生保健系统却有极大的影响。例如早在2000年，美国白喉破伤风疫苗停止生产导致正常的适龄儿童疫苗接种推迟了将近2年，使数百万儿童暴露在疾病的风险之下。再如2004年，英国的一家流感疫苗生产商因为不符合标准生产规则而关闭，导致当年美国市场流感疫苗供应量下降了近一半，当年流感患者激增。较近的2008年，肝素钠注射液（一种被广泛应用于外科手术病人的注射液）的储备短缺在美国导致了多起包括死亡在内的严重案例。在平时类似的药品短缺已经可以导致这样的结果，那么遇到诸如地震、洪水等自然灾害的，后果的严重程度更是不言而喻。2008年汶川地震、2013年雅安地震中若更多的基础消炎药品、食品、帐篷等基础生活品送到灾区，那么更多的生命可以得到挽救。

但是，类似基础药品、特种药品、化工材料等诸多物品往往在受国家政策调控、市场、生产等方面因素的影响下利润空间有限。姚立新等认为生产厂家往往同时生产多种产品或类似药品，其生产设备除了少数是专用型之外，大部分生产设备属于多用途和通用型。所以厂家通常都需要制定从长期的战略计划到短期的详细策略来管理企业的供应链［1］。根据Duffie D．和Pan J．的研究，在多种产品共用有限生产资源的情况下，制造商就会改变产品策略或者迁移生产资源来生产那些回报相对高和风险相对低的产品，这就使得那些低利润高风险的医药用品如流感疫苗供给短缺［2］。影响药品短缺的另一个因素是工业合并，它可以使得必需品短缺的情况变得更加糟糕，由于合并导致产品线越来越窄，重叠产品被停止生产，结果是某些特定的产品只有单一供应商。以美国疫苗市场为例，数据表明主要的疫苗制造企业从1980年的17家减少到2002年的5家，到2011年全美只有10家疫苗制造企业在生产各种不同的疫苗［2］。合并的结果使许多种类的疫苗都仅由一个制造商来提供，进而使整个供应链系统变得脆弱和运转不灵活。

基于以上原因，药品短缺已经成了欧美各国长期面临的难题。自2004年以来每年在美国发生的药品短缺的数量还在不断的持续增长中，参见美国社会药剂卫生系统的药品资源短缺中心的报告［1］。虽然药品短缺对制造商的影响很小，但对卫生保健系统却有极大的影响。Bennett B．和Cole G．研究认为在没有可替代药物的情况下，药物短缺可能改变或推迟对病人的治疗，即使在有可替代药物的情况下，也会增大出错的机会从而导致对病人不利的情况。最近的调查结果表明药物短缺不论其是否有可替代药物，都会对社会上参与卫生保健系统的每个人带来高风险［3］180－187。这些短缺所引起的各种结果还有可能进一步引发严重的社会和经济问题。因此政府应在预防类似必需品短缺的问题上起到积极作用。

目前，欧美各国首要的预防药品短缺的方法就是政府采购合同。以流感疫苗制造业为例，因其对生产环境的高要求、诸多的约束条件、相对的高风险和低回报，使流感疫苗制造让生产商敬而远之。这一点从全美目前只有4家生产流感疫苗的企业就可以看出来。为了满足部分与政府相关的流感疫苗的市场供应，美国政府每年花费上亿美元购买疫苗，其中也包括流感疫苗，分配给那些有特殊需求的部门、州、地区。通过这一手段，政府降低了疫苗供应的价格，同时提供了一个稳定的市场环境，减少了制造商的财务风险。

Chen W．和Sim M．通过研究提出政府干预企业生产的另一种可行的方法是政府回购［4］。例如在流感疫苗制造企业，因为受到很多不确定的因素影响，疫苗的需求是很难预测的，但制造企业仍不得不在生产前6个月对年度需求量进行预测。在这种情况下，制造商往往倾向于保守的生产计划，生产相对少量的产品来保证所生产的产品都可最终被市场吸收，从而减少大量生产带来的风险。这一情况经常会导致产量不能满足实际市场需求从而加重社会的负担。如果政府能够以一个合理的价格将生产出的多余的产品进行回购，将有助于产品供应的稳定，从而避免药物短缺。总的来说，这样做对政府和社会都是有好处的。

本文将重点分析上述两种政府干预手段。以往的文献大多只将政府干预作为博弈模型中一个参数，未对其结果进行详细研究。笔者从另一个角度，把政府干预作为一种手段来研究。政府干预企业投资选择的经济结果取决于政府多元目标与不同资本投向所形成资产的功能、用途、经济价值等属性之间的契合度 ，为了达到双赢，我们围绕这个最佳契合度进行研究。本文中，以发达国家美国的制药企业为例的原因是因为其有成熟的市场运作规则和制度。为此，我们建立了一个制药企业的决策问题的模型，以上所提到的在政策制定中都有所涉及，也就是说政府的采购合同和目录清单回购都被考虑在模型中。我们研究不同政策对制造商决策过程的影响，重点研究最终决定所带来的风险。风险测量使用制造商损失函数的条件风险价值模型。

本文余下的结构如下，在第二部分将给出全系统的描述以及模型的参数和变量。第三部分将回顾CVaR的定义及特性，通过最小化CVaR来规划构造制造商决策这一问题。第四部分将对模拟的结果进行分析并结合中国现状给出建议。最后一部分得出结论。

二、系统模型与参数

本文所考虑的系统可以简单地用图1表示。这个模型是以制造商为中心，其生产计划受市场与政府调控政策参数的影响，详细描述如下。

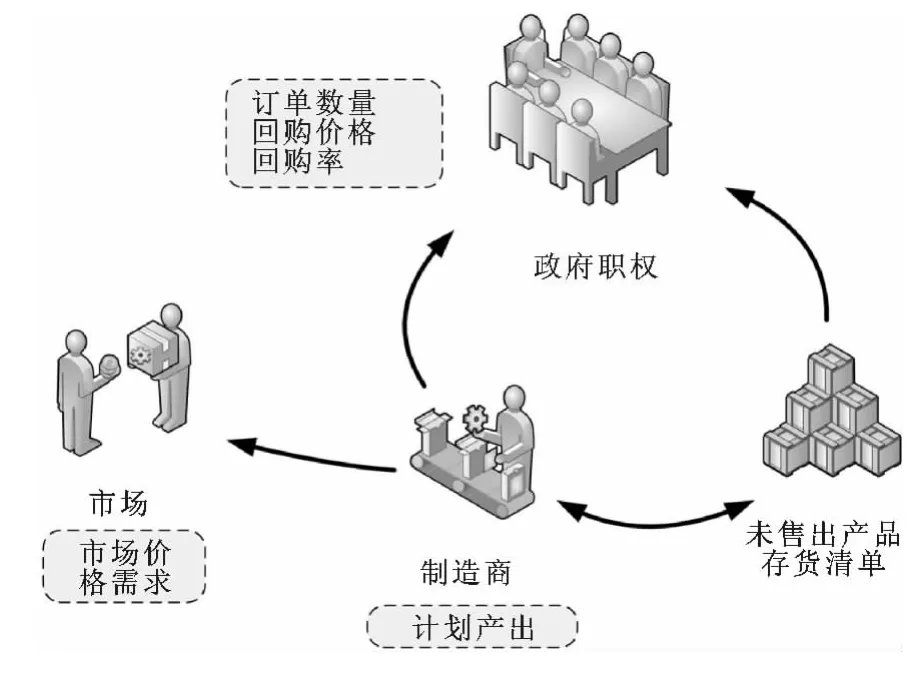
图1 全系统图解图

制造商：假设产品制造商同时生产高风险与低风险两种产品，必须为两种产品安排生产计划分配生产资源。在本文的模型中，我们假设制造商制定计划和资源调度时首要考虑的是最小化其金融风险。

市场：这里主要指市场上产品的价格和需求。每一种产品都有一个固定的已知市场价格，而需求量是服从已知分布的随机变量。

政府职权：政府职权以两种方式影响制造商的生产决策。一是以等同或低于市场价格订货；另一种方式是产品回购，也就是政府部门以低于生产成本的价格回购部分或全部厂家未能售出的产品，回购的价格和比例都由政府职权部门决定。

根据以上描述，模型中各个单位的调整参数和变量列举如下：

制造商：

参量：

CH：高风险产品的生产成本；

CL：低风险产品的生产成本；

IU：制造商投资的上限；

IL：制造商投资的下限；

R：制造商的预期收益；

LbH：生产高风险产品的最小产量

变量：

xH：计划生产的高风险产品；

xL：计划生产的低风险产品

市场：

参量：

PH：高风险产品的市场价格；

PL：低风险产品的市场价格；

dH：高风险产品的需求；

dL：低风险产品的需求

政府职权：

参量：

PB：政府回购价格．

SB：政府回购的比率

OG：政府预购风险产品的数量

应用这些变量模型中的约束条件如下：

预期收益约束条件：

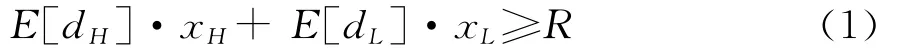
这个约束条件确保某些投资的预期收益。

总投资的约束条件：

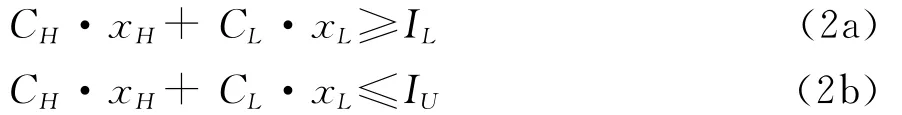
这个约束条件限定了制造商关于产品投资的上限和下限。

最小输出限制：

这个限定条件是用来保证高风险产品最小计划的生产量，以保证一定的规模经济。

如前面所述，制造商在制定生产计划的时候，主要考虑的是最小化财务风险。接下来我们就讨论如何进行具体财务风险的测量。

三、量化财务风险

本文利用著名的条件风险价值（CVaR）模型来测量制造商的生产计划的财务风险，在这一部分，首先给出了制造商的损失函数并证明其凸函数特性，接着给出了CVaR的定义和属性。

（一）损失函数和其凸性描述

随着决策变xH、xL和随机市场需求dH、dL变化的利润也是一个随机变量。根据第二节的描述，利润由两部分构成：1．常规销售获取的利润；2．政府回购获取的利润。我们取利润的相反数为损失函数，因此高风险产品的损失函数可以表述为：

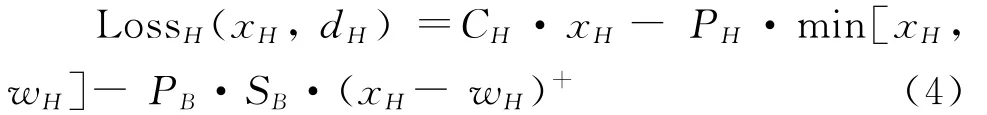
其中对任意实数a，a＋＝max［a，0］，wH＝max［OG，dH］是制造商获得政府采购订单后对产品需求的估计。

正如式（4）中表明，损失函数LossH（xH，dH）不是直接关于xH的凸函数。然而，LossH（xH，dH）可以重表示为xH的分段线性凸函数，这一结果将在定理1中给出。

定理1：在PH≥CH≥PB·SB的条件下，定义式（4）中高风险产品的损失函数等价于

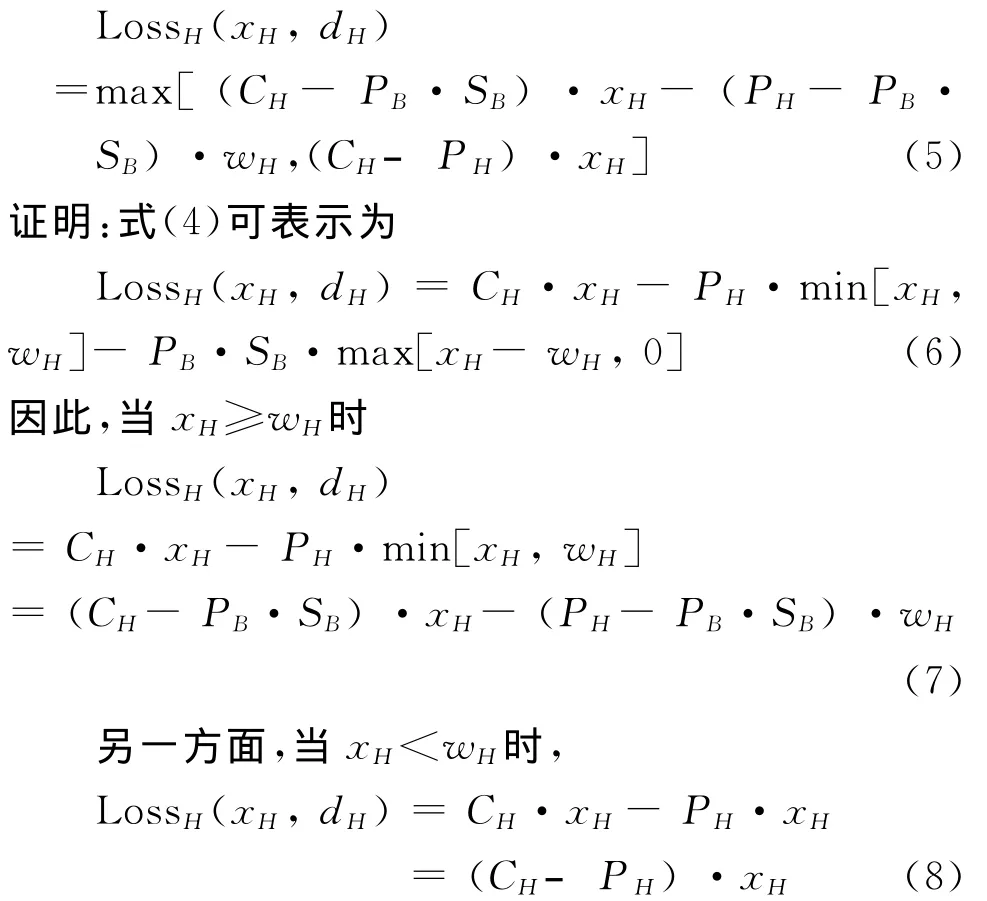
在PH≥CH≥PB·SB的条件下，LossH（xH，dH）可以用式（7）和式（8）来表示，它的大致图形如图2所示，很明显它与式（5）是相等的。

综上分析完成了证明。

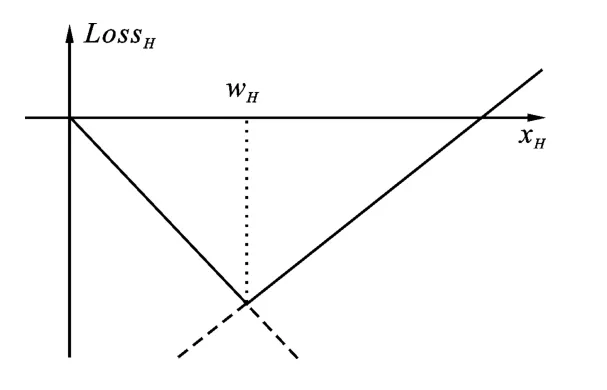
图2 损失函数LossH（xH，dH）图

要点1：在定理1中关于PB·SB的必要条件在PH≥CH≥PB·SB是十分合理的。如果这一条件不满足，制造商的生产计划仅通过简单的观察就能决定。

式（5）描述的损失函数很明显是关于产品计划产出的线性分段凸函数。与之相类似的，没有政府干预的低风险产品的损失函数可以表示为：

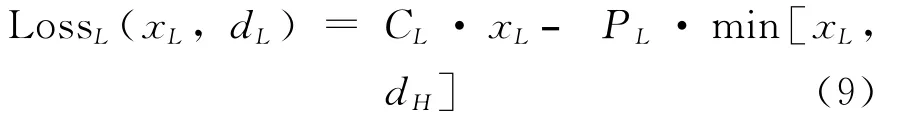
也是关于决策变量xL的线性分段凸函数。根据（5）式和式（9），整个系统的损失函数可以表示为：

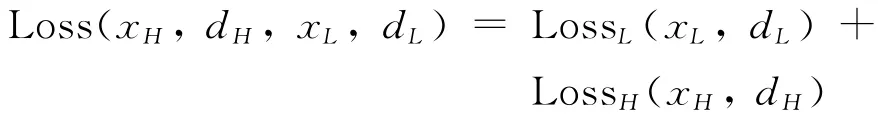
（二）条件风险价值（CVaR）

我们用系统的损失函数的条件风险价值来测量制造商生产计划的风险。首先我们对条件风险价值的定义和属性作一个简短的回顾。

CVaR被提出之前，在20世纪90年代风险价值模型（VaR）作为一种最著名的风险测量工具被广泛研究和应用［5］。损失函数L（x，d）包括一个决策向量x和一个随机向量d以及一个给定常数的0＜a＜1。损失函数的VaR被定义为：

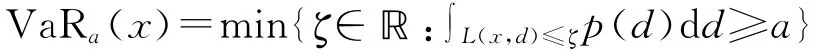
在这里p（d）是d的密度函数。在VaR的基础上，21世纪初，CVaR被提出来［6］，它的定义如下：

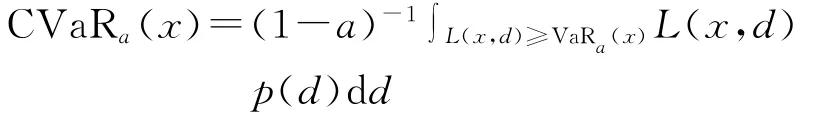
相比VaR，CVaR具有更多令人满意的数学特性。CVaR是具有连贯性的风险测量工具［7］。为了说明这一点，需要如下辅助函数。

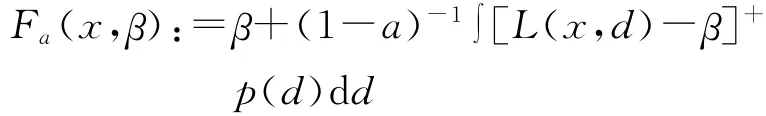
Huang D．等很好地研究了函数Fa（x，β）的特性以及它与VaR和CVaR的关系［8］。这些研究结果将在下面的定理中分别总结。正是由于CVaR具有这些良好的特性，使之被广泛应用于管理学各领域的研究中。

定理2：作为a的一个函数，Fa（x，β）具有凸性并且连续可微。当L（x，d）关于x具有凸性时，Fa（x，β）关于（x，β）具有凸性。

对于一个给定的x，与损失函数L（x，d）相关联的VaR和CVaR可被确定为：

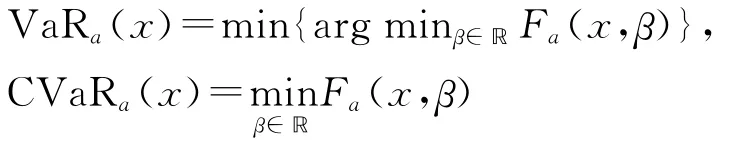
要点2：从定理2可以看出，通过最小化辅助函数Fa（x，β）来同时确定 VaR和 CVaR，此外，Fa（x，β）式中的多维积分也可以通过采样平均的方法来近似。

最终，制造商的生产计划最后变成以下两种形式：

我们以最优问题式（10）为基础进行了仿真分析。相应的分析和结果将在下一节中给出。

四、仿真结果与分析

本部分通过一个例子进行仿真分析。在这个例子中，制造商生产2种类似疫苗的产品，一种是高风险产品，一种是低风险产品。高风险产品类似于流感疫苗，需求是不确定的，只有在年末北半球是否发生疫情才能决定。低风险产品类似于常规疫苗，需求是稳定的，出生率等其它因素是可以估计的。在这个例子中，这两种产品的数据我们从Cˇerba′kova′的研究中获得并描述如下高风险产品的需求dH［9］817－822。我们假定它是截断常正态分布在区间［50，200］上，原始的正态分布均值为125（百万），方差75，表示为N（125，75）。低风险产品的需求dL也被取值为在区间［30 50］上的正态分布N（40，5）。其它的参数包括CH＝8，PH＝12，CL＝25，PL＝40。加之在所有的模型中a＝0．95。

（一）生产商无政府干预下的产品选择

在这个模型中，政府干预被假设为无效的。此外，R＝0并且LbH＝0因此约束条件1和3无效。制造商行为的目的集中在选择产品上。在约束条件2中IL的值从1 350增加到1 750，并且可以观察到随着总投资的增长，在高风险产品和低风险产品中总投资曲线是如何分布的。仿真的结果见图3，从图3中可以看出总投资增长越多，在低风险产品上的投资也越多。它表明了金融回报如果得到保障或者不是主要的关注重点，制造商总是尽量避免额外的风险［10］。这就可以解释为什么在1990年疫苗生产厂家一直停止交易。因此，期望某些药物保持一个稳定的供给，这些药物的风险应该降低至不至于厂家退出市场。在其余的部分，我们通过模型来分析政府干预和紧急供应对减少制造商风险的作用。

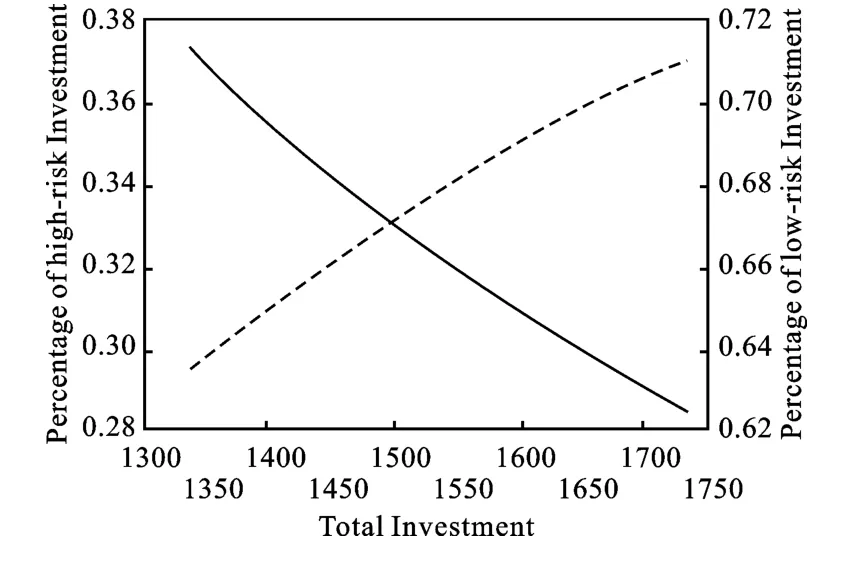
图3 总投资在不同产品中的分布图

（二）政府干预

1．采购合同。在这个仿真中，假设高风险产品为制造商的唯一产品，在没有政府回购的情况下，我们研究企业风险和对企业决策的影响。约束条件1和2无效，并且LbH在约束条件3中取值150以保持最小的产量。政府采购合同的取值OG从50到210，相应的计划输出和企业风险的变化情况在图4中标出。在图4中企业风险随着政府采购合同的增加而减小，由于最小产量的限制，计划输出没有改变。当政府采购合同超过最小产量后，企业风险以很小的比率持续减少，也就是企业的产出效益保持在一定的水平。如同我们期望的结果一样，由于政府的采购合同使得风险从企业转移到政府。不管怎样，政府部门没有面对更多的风险，因为其可通过防疫补助基金获益，也就是说从那些各州的卫生部门，某些大城市的防疫基金等处获得。

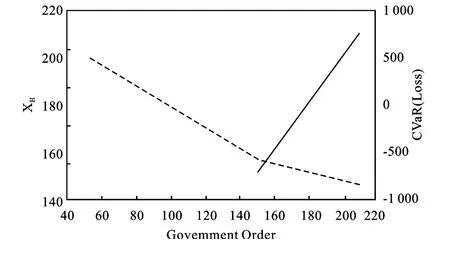
图4 生产输出和风险与政府采购量的关系图

2．回购政策。这个仿真和前一个相似，假设没有政府采购合同，而回购是有效的。政府回购比率为SB＝1并且回购价格在0到7．8之间变化。最小的产量也是150。采用政府回购，政府的损失函数可以简单的表述为PB（dH－xH）＋，并且这个损失的CVaR也可十分简单的计算。这个模拟的结果表明随着PB的变化，xH仍然保持为150，但是制造商和政府的CVaR改变了。回购价格PB的改变在图5中表示。从图5可以观察到制造商的风险随着PB的增加而减小，但是转移给政府的风险总是正相关的，并且与政府采购合同相比，其风险性更高。

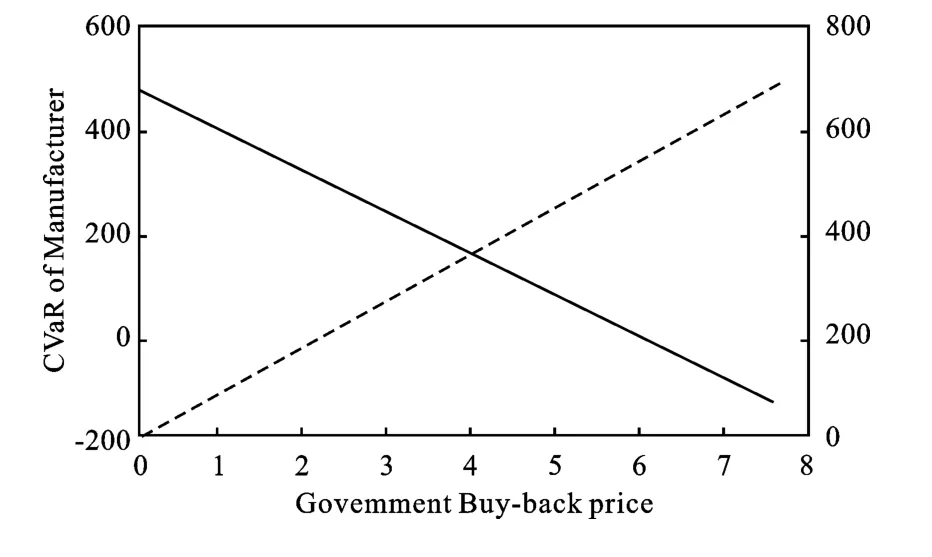
图5 制造企业与政府的风险与政府回购价格的关系图

通过上述分析可以看出政府干预可以很好地平衡企业效益与政府支出的关系，通过调整模型的输入参数，能够比较政府不同干预政策的结果。

五、结 论

本文将高风险必备产品制造企业的政府干预研究从理论研究扩展到实际研究层面上，以美国制药企业为例，提出了一个适合分析高风险必备产品生产工业的通用模型，并引入制造商损失函数的条件风险价值来测量其财务风险，为企业和政府制定决策提供理论依据。

将政府干预研究的结果作为公共政策评估的一种方式，本文提供了检验公共政策的一种新方法。通过这种方法，可以比较不同的政府政策，从中选出最优的政策。

在中国某些疫苗的制造业和市场还处在初期阶段，如果只采用国家投入生产高风险必备产品不符合市场规律，应该通过市场调节和政府干预相结合，通过立法或者是产业政策促进高风险临床必备药品的研发和生产，提高药品企业生产制造、改进创新的积极性。政府特别要加强关于药品短缺的立法建设，从法制层面明确药品短缺的主要责任人，建立药品短缺的信息发布平台，指导企业的研发与生产。

［1］ 姚立新，Garth Boehm，郑强．美国药品短缺及FDA采取的应对策略［J］．中国新医药杂志，2012，21（20）．

［2］ Duffie D，Pan J．An Overview of Value at Risk［J］．The Journal of Derivatives，1997，4（3）．

［3］ Bennett B，Cole G．Pharmaceutical Production－ An Engineering Guide［M］．Rugby：Warwickshire，2003．

［4］ Chen W，Sim M．Goad－driven Optimization［J］．Operation Research，2009，57（2）．

［5］ Fox E R，Birt A，James K B，et al．ASHP Guidelines on Managing Drug Product Shortages in Hospitals and Health Systems［J］．American Journal of Health－System Pharmacy，2009，66（15）．

［6］ Fox E R，Tyler L S．Managing Drug Shortage：Seven Years Experience at One Health System［J］．American Journal of Health－System Pharmacy，2003，60（3）．

［7］ Zhu S，Fukushima M．Worst－case Conditional Value－at－Risk with Application to Robust Portfolio Management［J］．Operation Research，2009，57（5）．

［8］ Huang D，Zhu S，Fabozzi F J，et al．Portfolio Selection under Distributional Uncertainty：A Relative Robust CVaR Approach［J］．European Journal of Operational Research，2003（1）．

［9］ Cˇerba′kova′．Worst－case VaR and CVaR．Operations Research Proceedings［C］∥Operations Research Proceedings，Heidelberg：Springer－Verlag，2006．

［10］Verderame P M，Elia J A，Li J，et al．Planning and Scheduling under Uncertainty：A Review Across Multiple Sectors［J］．Industrial ＆ Engineering Chemistry Research，2010，49（9）．