倾角对全玻璃真空管热水器温度场和流场的影响分析
2014-01-01云南师范大学太阳能研究所教育部可再生能源材料先进技术与制备重点实验室李仁飞高文峰刘滔林文贤
云南师范大学太阳能研究所 教育部可再生能源材料先进技术与制备重点实验室 ■ 李仁飞 高文峰 刘滔 林文贤
0 引言
近年来,我国的全玻璃真空管太阳能热水器产业发展迅速,在太阳能热水器市场中占据绝对主导地位。全玻璃真空太阳集热管是真空管热水器的核心部件,在较高温度下运行时,真空管热水器的热性能优于平板型热水器[1]。此外,真空管太阳热水器还具有热性能稳定、可在较低环境温度下运行、太阳光小角度入射下效率高等优点。但目前国内市场上真空管太阳热水器同质化现象严重。以安装倾角为例,多数家用真空管太阳热水器的安装倾角约在40°,并未考虑不同地区太阳能应用的最佳安装倾角。
真空管太阳热水器以其良好的集热和保温性能,近年来得到国内外众多学者的关注和研究。Jaisankar等[1]详细论述了太阳热水器的优势和提高其热效率的各种方法和技术;Morrison等[2]研究了真空管内日得热量的影响因素,并利用实验和数值模拟研究了真空管内自然对流的流动分布和温度分布;钟建立等[3]对真空管进行了二维数值模拟和实验对比,并可视化地揭示了太阳能真空集热管闷晒下的流场和温度场的变化规律;Morrison等[4]利用PIV实验和数值模拟分析了单管内的流动特征,发现单管内的流速对水箱内的温度分层影响很大,并得出单管内的热流分布是影响流动结构和流速的一个重要参数的结论;而王志峰等[5]对全玻璃真空管内的流动与换热情况进行了三维数值模拟。
由于真空管热水系统内部对流换热过程的复杂性,目前国内外对其换热和流动机理的研究还甚少,也没有应用太阳载荷模型进行研究的研究结果报道。本文在前人研究的基础上,以家用真空管太阳热水器中的其中一支及对应流体区域为研究对象,建立三维单只真空管热水器数值模拟模型,在模型中加载太阳载荷模型,既考虑直接辐射、漫射太阳辐射和地面反射,同时也考虑系统内部散射和漫射及太阳的位置变化等,使计算更接近实际。本文对安装倾角对真空管热水系统流场和温度场的影响进行研究,不仅可揭示真空管内部的传热机理,还可为真空管热水系统传热传质和结构参数优化,以及效率的提高提供一些科学依据。
1 物理模型
本文以目前市场上一种常见的全玻璃真空管型太阳热水器为研究对象,利用数值模拟研究加热期间真空管及水箱内流体的流动特征。所研究的全玻璃真空管热水系统的截面结构如图1所示。水箱内径为360 mm,保温层厚50 mm;真空集热管管间距为80 mm,其外径58 mm,内径47mm,管长1800 mm。真空管主要由内管和外管组成,内管顶部和外管相接,底部封闭并由弹簧卡片固定。内管外壁表面涂有高吸收率和低发射率的选择性吸收涂层,内、外管之间抽真空,减少对流换热和导热损失并保证集热系统的质量和寿命。

图1 全玻璃真空太阳热水器截面结构示意图
2 数值模拟模型及求解
2.1 数值模拟模型
真空管热水器中集热系统由多支真空管等间距并排组成。考虑到计算的方便及实际运行时的状态,这里根据以上所述的真空管家用太阳热水器的物理模型,在建立数值模拟模型前作如下简化处理[6-9]:1)计算区域简化为管间距为80 mm的单只真空管和储热水箱组成;2)真空管由罩玻璃管和外壁面涂有选择性吸收涂层的内玻璃管组成;3)忽略真空夹层的导热和对流换热及邻管之间的阴影遮挡。
由于所研究的真空管太阳热水器在加热运行时主要传热方式为自然对流,其流动状态利用雷诺数Re=VDH/v来判断流动是层流还是湍流。式中,V为管截面平均流速;DH为管直径;v为水的运动粘度。计算结果表明,Re≤2300,应为层流状态,因而选择层流模型来计算。在辐射模型中,只有DO模型可计算半透明介质。本模型中的罩玻璃管为半透明介质玻璃,所以辐射模型采用DO模型。
Fluent提供了两种选项来计算太阳载荷:晴朗天气条件法和理论最大值法。本文选择晴朗天气模型(假设没有云层,晴天指数为1),计算直接太阳辐照为Edn=A/eB/sinα。其中:A和B分别为大气质量为0时的太阳辐照和大气消光系数,其值根据在无云时地球表面的数据得到;α为太阳高度角。太阳载荷模型采用太阳射线追踪模型,地理位置设置为昆明的地理纬度(北纬25°,东经102°,东8区),计算得到直接太阳辐照度为883.15 W/m2。
2.2 边界条件
真空管内由导热引起的热损失相对于辐射热损失来说较小,可忽略内管热损失。用于数值模拟的对应边界条件设置如表1所列。水的密度变化通过采用Boussinesq假设实现,且假设水箱和真空管底部的弹簧夹没有热损。

表 1 用于数值模拟的单只真空管热水系统边界条件
选择压力求解器、绝对速度、瞬态、重力加速度沿y的负方向,即y=-9.8 m/s2,环境温度恒定为300 K。
2.3 求解方法
计算时应用分离式求解器,选择压力速度耦合的SIMPLEC算法。压力采用PRESTO!离散方法,动量、能量方程选择二阶迎风格式。为了得到更好的收敛效果,适当修改松弛因子。计算的时间步长为0.5 s,时间步数为7200,最大迭代步数为450,计算网格总数为308656,网格结点数为306119。
3 计算结果分析
3.1 真空管热水器中心面上的温度场和流场分布
图2和图3分别为加热了3600个时间步(即1 h)时刻,倾角为 30°、45°和 60°的单只真空管热水器系统的温度和速度分布图。
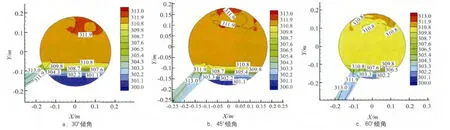
图2 不同倾角下真空管热水器温度分布
从图中可看出,在真空管内,存在明显的两股冷热流体。由于热浮力的作用,具有较高温度的热水沿真空管上壁进入水箱上部,而温度较低的冷水从水箱下部沿真空管下壁面流入真空管内,在整个真空管及储热水箱内形成封闭的自然对流循环。在靠近真空管管口的上壁面出现温度最大值,真空管内部水温总体比水箱内水温高。在水箱内部真空管出口以上区域的水经真空管上部流出的热水被逐渐加热,而在真空管出口下部存在一个滞留区,该区域的水只能通过导热传热。从图3中可看出,热水从真空管的上壁面射入水箱上部。随着系统倾角的增大,真空管管口冷热水的掺混越明显。当倾角增加为60°时,在真空管与水箱连接处形成明显涡流,使流体循环受到一定程度的阻碍,同时使能量损失增大,进而使进入水箱内水的温度和速度均有所降低。

图3 不同倾角下真空管热水器速度分布
3.2 真空管与水箱连接处截面流动速度分析
图4为真空管与水箱连接处真空管截面径向速度分布图。图中定义朝水箱方向为轴向速度的正向,真空管的中心轴为原点,真空管上半部分为x轴的正方向。
从图4可知,真空管上半部分的速度比下半部分大。由于冷热流体在同一个流道流动且流动方向相反,在靠近真空管的中心位置处速度最小。真空管内靠近内壁面存在明显的速度边界层。在真空管与水箱连接处的截面上,倾角为30°的系统相对比倾角为45°和60°的系统速度小,而倾角为45°和60°的集热系统的速度很接近。这是因为沿真空管内水流动的方向上,随着倾角的增大,重力在水流动方向上的分力也相应增大。但在60°时系统的温度有所降低,导致45°和60°的系统的流速很接近。这一计算结果与文献[4]中的PIV测量结果相一致,虽然文献[4]中的PIV测量结果比本文的计算结果小,但这一差别主要是由于数值模拟作了简化和理想化的假设造成的。总体而言,本文的数值模拟计算结果和实验结果较为吻合,表明本文所建立的数值模拟模型是可靠的。

图4 真空管与水箱连接处径向速度分布
3.3 水箱内温度场和流场分析
图5为x=0、z=0、y轴从-0.2~0.2 m所切取的沿水箱垂直方向上的温度分布,而图6为不同倾角下z=0.03 m处切取的水箱内的速度分布。从图中的模拟结果可看出,不同倾角下水箱内的温度和速度分布趋势一致。由于热浮力作用和重力作用,水箱底部温度最低,顶部温度最高;从水箱底部到顶部,温度和速度都逐渐增大。水箱底部滞留区内冷热水几乎没有掺混,相对温度和速度都很小。而随着集热系统倾角的增大,水箱内的速度有先增后减的趋势。

图5 30°、45°、60°倾角下水箱垂直方向温度分布

图6 不同倾角下真空管热水器速度分布(z=0.03 m)
此外,60°倾角时水箱内的掺混更明显。30°倾角时水箱底部滞留区厚度约为0.04 m,45°倾角时该厚度减小至约0.03 m,而60°倾角时此厚度进一步减小至约0.02 m;即随着倾角的增大,水箱底部滞留区的体积逐渐减小。这是因为真空管插入水箱的管口正对水箱中心位置,倾角不同插入水箱的位置也不同。
4 结论
在热浮力和重力的作用下,家用真空管热水器的真空管内热水沿管的上壁向上流动,形成射流流向水箱上部;而冷水从水箱下部沿真空管的下壁面流入真空管内,在整个真空管及储热水箱内形成封闭的自然对流循环。真空管内部水温总体比水箱内水温高,且在真空管管口的上壁面出现温度最大值。真空管上半部分的速度比下半部分大。由于冷热流体在同一个流道流动且流动方向相反,在靠近真空管的中心位置速度最小。倾角为30°的系统相对比倾角为45°和60°的系统内的流速小,倾角为45°和60°的系统管内流速很接近,且倾角为45°的集热系统水箱内的平均温度比倾角为60°的高。说明对于真空管热水系统来说,安装倾角多数约为40°是合理的,增加倾角基本不会提高系统温度和流速。
加热区间水箱由顶部到底部存在很明显的温度分层,在储热水箱底部存在一个滞留区,该区的水几乎不流动,主要依靠水箱内从顶部到底部的温差导热传热而被加热。30°倾角时水箱底部滞留区的厚度约为0.04 m,45°倾角时水箱底部滞留区的厚度约为0.03 m,60°倾角时水箱底部滞留区的厚度约为0.02 m。因此,随着集热系统倾角的增大,水箱底部滞留区的体积逐渐减小。
[1] Jaisankar S, Ananth J, Thulasi S, et al. A comprehensive review on solar water heaters[J]. Renewable and Sustainable Energy Reviews, 2011, 15:3045-3050.
[2] Morrison G L, Budihardjo I, Behnia M. Water-in-glass evacuated tube solar water heaters[J]. Solar Energy, 2004, 76:135-140.
[3] 钟建立, 付丽霞, 雷进波. 全玻璃太阳能真空集热管流场和温度场的可视化研究[J]. 浙江大学学报(农业与生命科学版),2005, 31(3): 351-354.
[4] Morrison G L, Budihardjo I, Behnia M. Measurement and simulation of flow rate in a water-in-glass evacuated tube solar water heater[J]. Solar Energy, 2005, 78: 257-267.
[5] 王志峰. 全玻璃真空管空气集热器管内流动与换热的数值模拟[J]. 太阳能学报, 2001, 22(l): 36-38.
[6] 闫素英, 田瑞, 于文艳, 等. 全玻璃真空管太阳能热水器流动与换热的数值模拟[C]. 中国工程热物理学会学术会议论文集, 2011.
[7] 闫素英, 田瑞, 于文艳, 等. 全玻璃真空太阳能热水器内流场的影响因素分析[J]. 工程热物理学报, 2010, 31(4): 642-643.
[8] 张涛, 闫素英, 田瑞, 等. 全玻璃真空管太阳热水器数值模拟研究[J]. 可再生能源, 2011, 29(5): 10-14 .
[9] 郭超, 秦朝葵, 吕赵键. 真空管太阳能集热系统温度场、速度场模拟[J]. 煤气与热力, 2011, 31(l0): 12-15.
