基于GM（1，3）模型的树木生长量预测

梁 彭 ，冯仲科 ，徐伟恒 ,2，刘波云

(1.北京林业大学 测绘与3S 技术中心，北京 100083；2.西南林业大学 计算机与信息学院, 云南 昆明 650224)

基于GM（1，3）模型的树木生长量预测

梁 彭1，冯仲科1，徐伟恒1,2，刘波云1

(1.北京林业大学 测绘与3S 技术中心，北京 100083；2.西南林业大学 计算机与信息学院, 云南 昆明 650224)

本研究在GM（1, 1）模型的基础上，运用GM（1,N）系统综合预测模型，以解析木数据包括龄级、树高、胸径、材积数据数列为基础，建立预测树木生长量的GM（1, 3）综合预测模型, 并在MATLAB下编写GM（1, 3）模型程序，实现了模型运算预测结果用后验差检验法进行检验。结果表明，本模型预测精度较好，利用此模型进行树木生长量预测是可行的。

树木生长量；预测；灰色模型；GM (1, 3)

现阶段世界各国对合理利用森林资源都极其重视。要长期合理使用森林资源，必须了解对森林树木的生长动态过程。然而林分是一个结构非常复杂的生态系统，其生长周期长，这样就使营林的难度有所增加。因此，在制定正确的营林方案之前，必须建立林分生长量预测模型，用来掌握林分的结构和动态生长变化规律。

灰色预测模型（Grey Model），简称GM模型。是指由于环境对系统的干扰，系统信息中原始数据序列往往呈现离散情况，离散数列即为灰色数列或称灰色过程，灰色理论利用较少的或不确切的表示系统行为特征的原始数据序列作生成变换后建立微分方程。它揭示了系统内部事物连续发展变化过程，是一个近似微分、差分方程的模型，是建模思路和方法上的创新。一般是指 GM（1,1）模型及其扩展形式，GM（1,N）模型表示1阶的，N个变量的微分方程模型[1-3]。

本研究利用G（1，3）模型预测树木生长量，目的在于减少对活立木的伐倒后的破坏性实验，充分利用已有数据，实现树木生长量的预测，提高预测精度。

1 树木生长量预测模型

1.1 GM(1,3)模型建模过程

（1）一次累加生成∶通过数列间各时刻数据的依次累加得到新的数据与数列。对原始数列X(t),X(t)={X(1),X(2),…,X(n)}，进行一次累加生成，以弱化其随机性和波动性，强化其规律性，得累加生成数列Y(t)。

（2）累减生成：将累加生成数列还原成非生成数列。X(0)(ti)=X(1)(ti)-X(1)(ti-1) (i=1,2,…,n)。

（3）均值生成：对累加数据列作均值生成，得均值数列Z(t)。

（4）对于林木的材积（X1）、树高（X2）、胸径（X3）的时间序列数据，建立GM(1,3)模型。

微分方程

1.2 模型精度检验

1.2.1 后验差检验

原始序列标准差S1

1.2.2 模型精度检验等级

使用后验差检验模式精度后，得出树木树高、胸径、材积的指标，详细结果见表1。

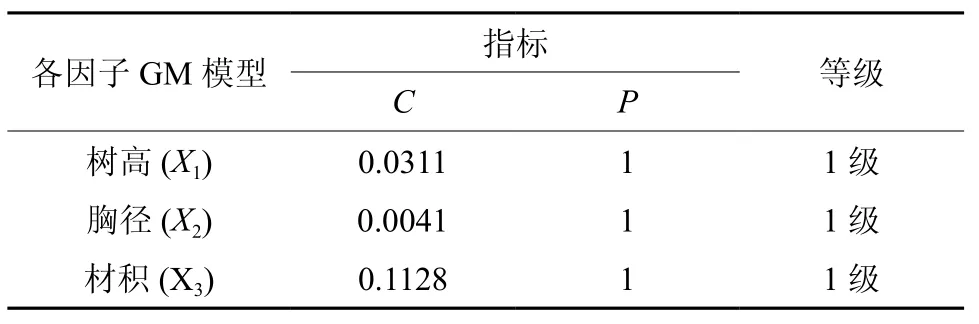
表1 GM模型精度检验情况Table 1 Results of GM model accuracy test

2 树木定期增长预测模型的建立

GM(1,3)预测模型为

X(1)(k+1)=[ X(0)(1)-3.468 2X(1)(k+1)-1.652 6X(1)

1123(k+1)] e-2.24k+4.6224 X2(1)(k+1)+1.532 5X3(1)(k+1)。（8）

3 模型建立后预测树木生长量

在选择的某林场的林地内选定50个标准地，而每个标准地的面积为800 m2，在每个标准地选取两株树木落叶松进行树干解析，以每5年为一个龄阶，测量选定树木各时期树高、胸径、材积的定期生长量，算出各因子的平均值，以此为依据建立树木定期长生量的预测模型。

3.1 测量树木各时期树高、胸径、材积的定期生长量

通过测量解析得出树木各时期树高、胸径、材积。详细结果见表2

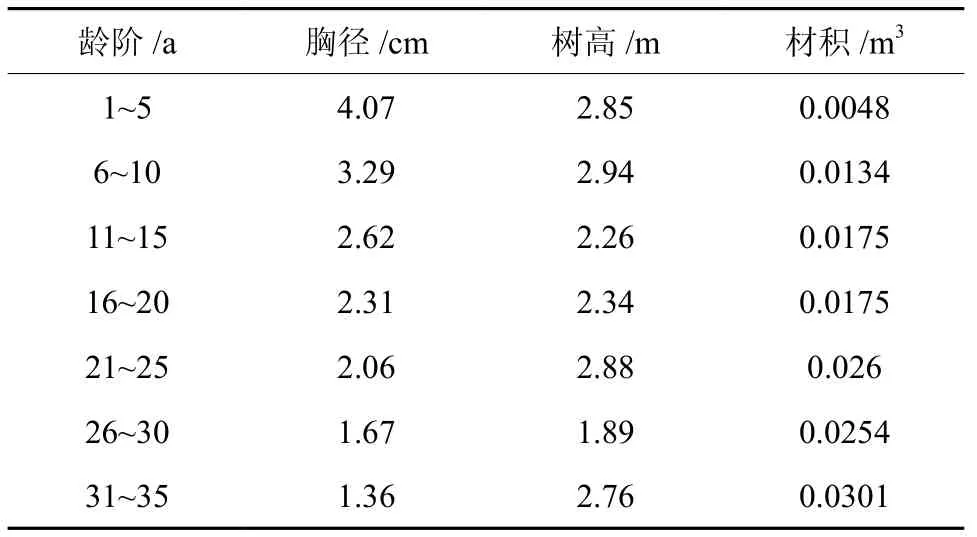
表2 树木各时期树高、胸径、材积情况Table 2 Tree height, diameter at breast height, volume growth of trees in various periods

3.2 利用模型预测树木的生长量

在模型构建好之后，预测树木的生长量，并将预测值与实际值相比较，详细结果见表3。

4 精度验证

经过验证后方差比为：

小误差概率：

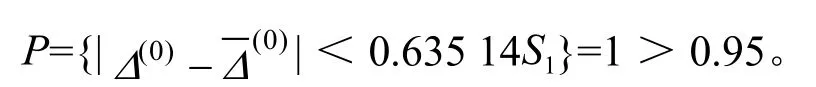
可以得出构建的GM（1，3）模型精度较好，结果可靠。

表3 生长量预测值与实际值Table 3 Comparison of prediction values and true values

5 GM（1，3）模型计算机程序

在MATLAB下的编写GM（1，3）模型计算机程序，程序如下：

clc

clear

%原始数据输入；

x0=[55.1;54.7;52.2;54.1;54.1;54.5;55.0];

n=7;

%由数列x0生成数列x1;

s=0;

for i=1∶n

s=s+x0(i);

x1(i)=s;

end

%由数列x1生成矩阵C和A；

for j=1∶n-1

C(j,1)=x1(j+1);

A(j,1)=x1(j);

A(j,2)=1;

end

%计算出估计值a1,a和u;

beta=inv(A'*A)*A'*C;

beta1=beta(1);

beta2=beta(2);

%求a,u值；

a=-log(beta1);

u=beta2/(1-beta1)*a;

%求出数列x1的预测值数列x2;

m=input('m=');

for k=0m-1)

x2(k+1)=(x0(1)-u/a)*exp(-a*k)+u/a;

end

%求出原始数列x0的预测值数列x3;

x3(1)=x0(1);

for k=1m-1)

x3(k+1)=(1-exp(a))*(x0(1)-u/a)*exp(-a*k);

end

%残差数据输入；

d0=[-0.3437-0.2226-0.3409-0.2997-0.0000];

k0=3;

%由数列d0生成数列d1;

sum=0;

for i=1n-k0+1)

sum=sum+d0(i);

d1(i)=sum;

end

%由数列d1生成矩阵C1和A1；

for j=1n-k0)

C1(j,1)=d1(j+1);

A1(j,1)=d1(j);

A1(j,2)=1;

end

%计算出估计值b,a1和u1;

b=inv(A1'*A1)*A1'*C1;

b1=b(1);

b2=b(2);

a1=-log(b1);

u1=b2/(1-b1)*a1;

%求出数列d1的预测值数列d2;

for k=0n-k0)

d2(k+1)=(d0(1)-u1/a1)*exp(-a1*k)+u1/a1;

end

%求出原始数列d0的预测值数列d3;

d3(1)=d0(1);

for k=1∶(m-1)

d3(k+1)=(1-exp(a1))*(d0(1)-u1/a1)*exp(-a1*k);

end

%求出原始数列x0的修正预测值数列x4;

x4(1)=x0(1);

for k=1∶(m-1)

if k>=k0

x4(k+1)=x2(k+1)-a1.*d3(k-k0+1)+u1;

else x4(k+1)=x2(k+1);

end

end

%求出原始数列x0的预测值数列x3;

x3(1)=x0(1);

for k=1∶m-1

x3(k+1)=(1-exp(a))*(x0(1)-u/a)*exp(-a*k);

end

x3

%残差检验；

for k=1∶n

d(k)=x1(k)-x4(k);

end

d

%相对误差；

for k=1∶n

e(k)=abs(d(k)/x0(k))*100;

end

e

s5=0;

for i=1∶n

s5=s5+d(i);

end

p=1/n*s5

%后验检验；

s1=0;s3=0;

for k=1∶n

s1=s1+x0(k);

end

for k=1∶n

s3=s3+d(k);

end

mean1=1/n*s1;

mean2=1/n*s3;

s2=0;s4=0;

for k=1∶n

s2=s2+(x0(k)-mean1)^2;

end

for k=1∶n

s4=s4+(d(k)-mean2)^2;

end

sigma1=sqrt(1/n*s2)

sigma2=sqrt(1/n*s4)

c=sigma2/sigma1

p1=0.6745*sigma1;

sum=0;

for k=1∶n

if abs(d(k)-mean2)

sum=sum+1;

else sum;

end

end

p2=sum/n

6 结 论

灰色预测实际上是一种时间序列模型预测[4-7]。理论上说，任何预测对象，只要能够从中抽象出表征系统特征的时间序列，都能够采用它进行预测，并且这种预测方法是一种简单、经济、可靠并且预测精度比较高的预测方法[8]。但是，实际上它对原始数据序列有一定的要求[9]。要求数据序列比较“规矩”，未来的数据要和过去的以及现在的数据有相同的发展趋势，上下波动不要太大，否则，会在某一时刻产生较大的偏差[10-12]。

本研究详细论述了系统综合预测模型GM （1, 3）的建立过程，用后验差检验法对预测结果进行了检验，预测精度较好，表明应用预测模型所得的预测值与实际值吻合良好，模型合理，表明此模型对树木生长量的预测有一定应用价值。而且利用MATLAB进行了编程计算，实现了树木生长量预测，减少了人工计算强度。本模型及程序的构建对于林业部门掌握林分树木的生长量及对林分进行综合预测有一定的帮助，预测模型可以对落叶松的树高、胸径、材积的定期生长量进行长期预测，具有良好的实际应用价值。

[1]刘思峰 , 谢乃明 . 灰色系统理论及其应用 [M]. 北京 ∶ 科学出版社 , 2008.

[2] 刘金升, 左德元. GM(1,1)模型与灰色Verhulst模型在路堤沉降预测中的探讨 [J]. 四川建筑 , 2006, 26(1)∶ 69-73.

[3]章文波, 陈红艳. 实用数据统计分析及SPSS12.0应用[M]. 北京 ∶ 人民邮电出版社 , 2006.

[4]陈 峰 , 胡振琪 , 马 彬 , 等 . 灰色系统理论在林业用地预测中的应用 [J]. 沈阳农业大学学报 , 2006, 37(1)∶ 57-60.

[5]DENG Ju-long. Significance of difference information in grey theory[J]. The Journal of Grey System, 1999,(3)∶256.

[6]方丽君 , 吴 中 . GM(1, 3)模型在交通系统公路客运量预测中的应用 [J]. 公路交通科技 , 2006,23(3)∶163-166.

[7] 王文斗. 辽宁东部山区落叶松人工林生长量预测模型的研究[J]. 林业科技 , 1998, 23(5)∶12-13.

[8] 惠淑荣,于洪飞. 日本落叶松林分生长量Richards生长方程的建立与应用 [J]. 生物数学学报，2003,18(2)∶ 204-206.

[9] 艾训儒,沈作奎. 中亚热带日本落叶松生物量、生长量研究[J]. 湖北民族学学报：自然科学版，2001,19(2)∶ 20-22.

[10] 汤国安 , 龚健雅 , 陈正江 , 等 . 数字高程模型地形描述精度量化模拟研究 [J]. 测绘学报 , 2001, 30(4)∶ 361-165.

[11] LΙANG Wen-Ju, LΙ Qi, JΙANG Yong, et al. Effect of cultivation on spatial distribution of nematode trophic groups in black soil[J]. Pedosphere, 2003, 13(2)∶ 97-102.

[12] David B K. High order Ιnterpolation of Regular Grid Digital Elevation models[J]. Ιnternational Journal of Remote Sensing，2003,24(14)∶2981-2987.

[13] 熊启明 , 杨柳青 , 陈 伟 , 等 . 基于 GΙS 的树木三维模型研究[J]. 中南林业科技大学学报 , 2011, 31(4)∶ 174-177.

[14] 高 原 , 冯仲科 , 仇 琪 , 等 . 基于 GM(1,1)的华山松生长量预测研究 [J]. 中南林业科技大学学报 , 2013, 33(6)∶ 94-96.

Tree growth prediction based on GM (1,3) model

LΙANG Peng1, FENG Zhong-ke1, XU Wei-heng1,2, LΙU Bo-yun1
(1. Mapping and 3S Technology Center, Beijing Forestry University, Beijing 100083, China; 2. Computer and Ιnformation Ιnstitute, Southwest Forestry University, Kunming 650224, Yunnan, China)

Based on the GM (1, 1) model, by using the GM (1,N) system integrated prediction model, the GM (1, 3) integrated prediction model of tree increment was set up according to the analytic trees data such as age class, tree height, DBH and wood volume, and the GM (1, 3) model program for the prediction was composed based on MATLAB. The predictive results from model calculations were examined by posterior difference testing method. The results show that the presented model had better prediction accuracy, and it is feasible for the model to be used to predict tree increment.

tree growth increment; prediction; grey model; GM (1, 3) model

S711

A

1673-923X(2013)12-0077-05

2013-05-14

林业科技成果国家级项目推广“都市森林景观三维可视化表达技术示范推广”（201146）

梁 彭（1989-），男，山西人，硕士，主要研究方向为3S技术集成与应用研究

冯仲科（1962-），男，甘肃人， 博士生导师，主要研究方向为3S技术研究；E-mail：fenzhongke@126.com

[本文编校：吴 彬 ]