一种光伏并网逆变器的混合控制策略研究

张 震，王久和，马先芹

（北京信息科技大学 自动化学院，北京 100192）

引言

光伏并网逆变器控制策略的好坏直接影响并网电能质量的好坏。单级式光伏并网逆变器控制一般有两个基本控制要求：一要保持直流侧电压稳定；二要实现并网电流控制（网侧单位功率因数正弦波电流控制）[1]。逆变器控制策略多采用双闭环控制控制策略[2-6]，文献[2，4]电压外环采用PI控制策略，由于并网逆变器直流侧电压受环境和光照强度的影响，直流侧电压存在超调、响应时间慢。文献[5，6]提出了电压外环采用自抗扰技术的控制策略，由于采用二阶自抗扰模型，可调参数多，难以实现；电流内环采用PI反馈解耦，虽然也能实现解耦，由于前反馈本身是一种削弱耦合的补偿控制并且解耦的性能取决于系统参数，无法实现真正的解耦[1]。文献[7，8]采用无源控制理论对对逆变器进行解耦控制，根据光伏并网逆变器的内部互连结构和耗散性，从能量的角度去控制能量在系统中的重新分布，收到了良好的控制效果。

针对以上特点，本文提出了电压外环采用自抗扰控制策略保持直流侧电压稳定和利用无源控制策略进行电流解耦控制的光伏并网逆变器控制策略。仿真和实验结果表明，基于自抗扰和无源控制的光伏逆变器控制策略是可行的。

1 光伏并网逆变系统拓扑结构及建模

单级式光伏并网逆变器拓扑结构如图1所示。由图1光伏并网逆变器拓扑结构可知，在三相平衡电网电压情况下，光伏并网逆变器在三相abc坐标系中的数学模型为[7]

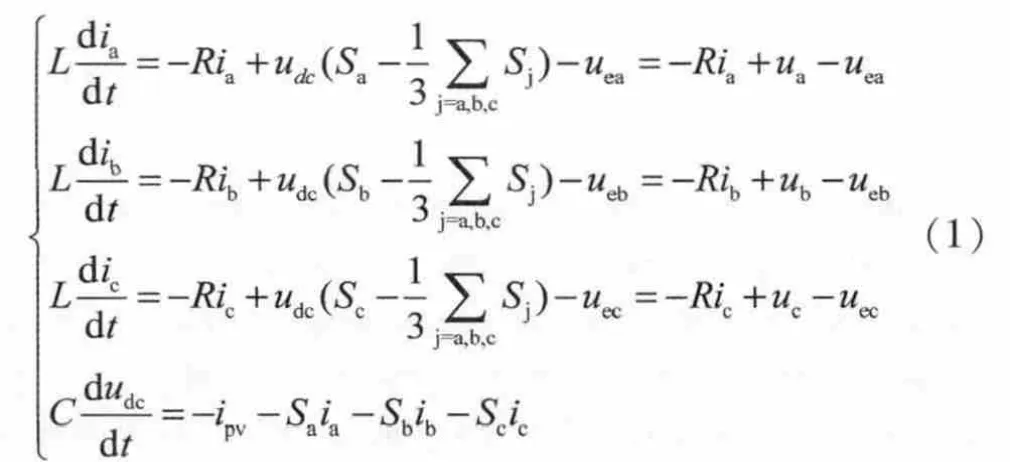
上式中，Sa，Sb，Sc为逆变器的开关函数，Sj定义为单极性二值逻辑开关函数，Sj(j=u,v,w)=1时，上桥臂导通，下桥臂关断，Sj=0时，上桥臂关断，下桥臂导通。L为输出电抗器，R为电阻与逆变系统内阻等效电阻，udc为直流侧母线电压，ipv为光伏阵列所提供的直流电流，idc为流入逆变器的电流，ia，ib，ic逆变器输出三相电流，ua，ub，uc为逆变侧三相交流相电压，uea，ueb，uec为电网侧三相交流相电压。

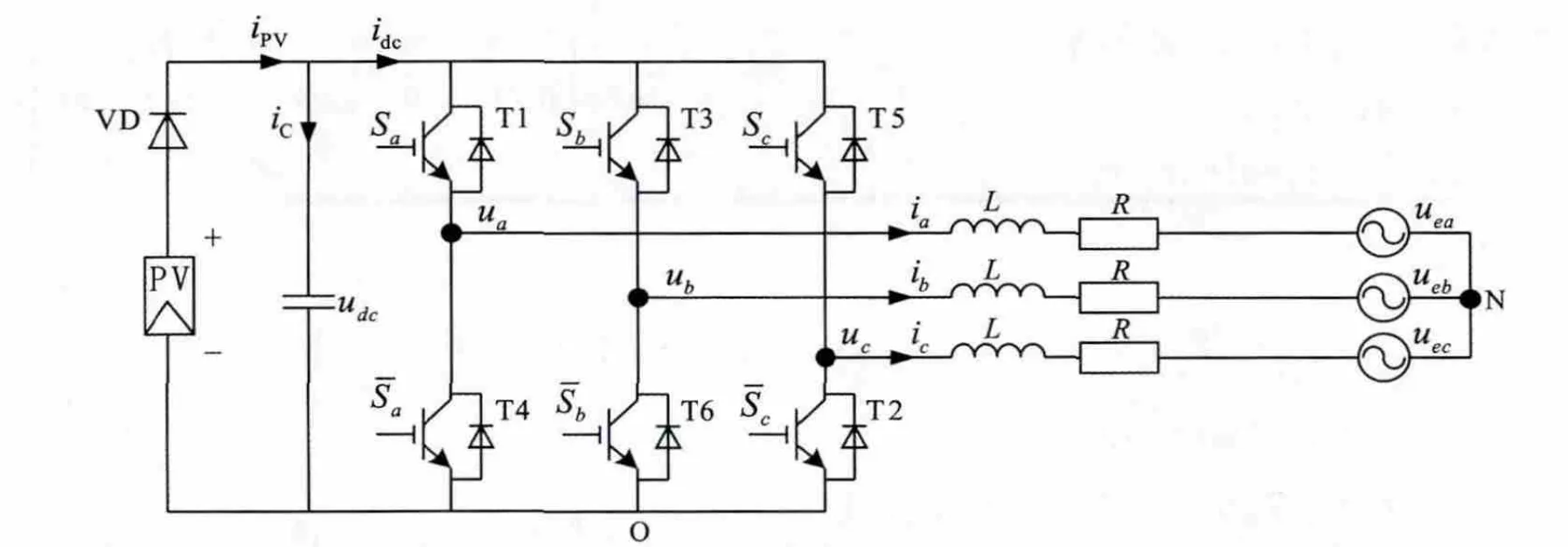
图1 光伏并网拓扑结构图

由于在三相abc坐标系的数学模型中存在时变的三相正弦交流电压，为了便于控制器的设计，通过变换矩阵

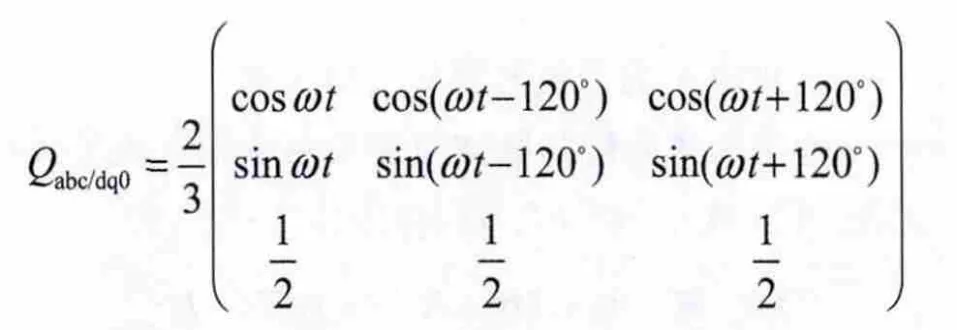
将其转换到两相同步旋转dq坐标系数学模型为

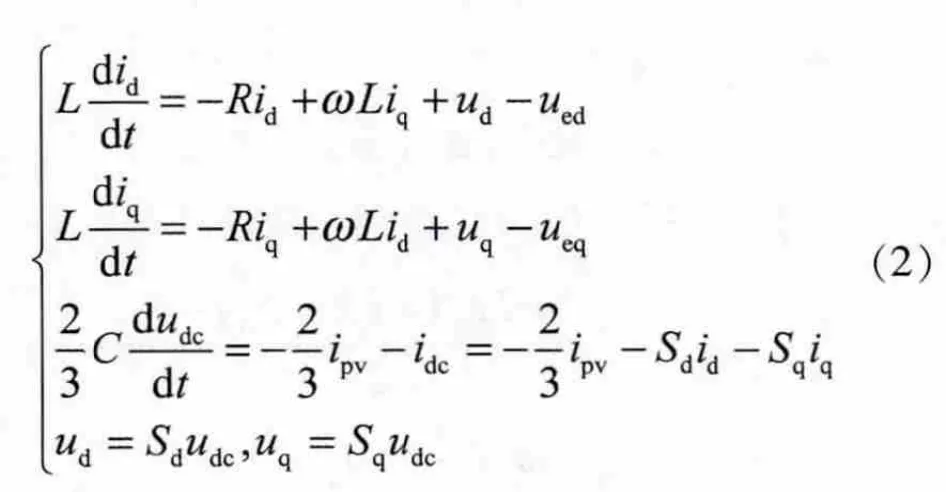
上式中 id，iq为输出端电流在 dq 轴分量，ued，ueq为输出端电压在dq轴分量，Sd，Sq为开关函数在dq轴分量。

2 光伏并网逆变器控制器设计

2.1 自抗扰控制器及设计

自抗扰控制器一般包括跟踪微分器（TD）、扩张状态观测器（ESO）和非线性状态误差的反馈控制律（NLSEF）[9]。微分跟踪器的作用是安排过渡过程并给出此过程的微分信号；扩张状态观测器是对系统的状态和扰动进行估计；非线性状态误差反馈控制律对获得的扰动分量进行补偿[10]。典型的一阶自抗扰控制器结构图如图2所示[11]。

设一阶被控系统方程为

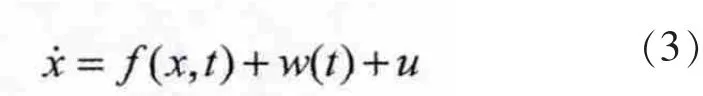
式中：f(x,t) 为未知函数；w(t)为未知扰动；x(t)为可量测被调量；u为控制量。可以得出如下的自抗扰控制器一般表达式。

跟踪微分器方程为

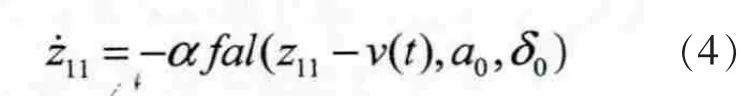
扩张状态观测器方程为

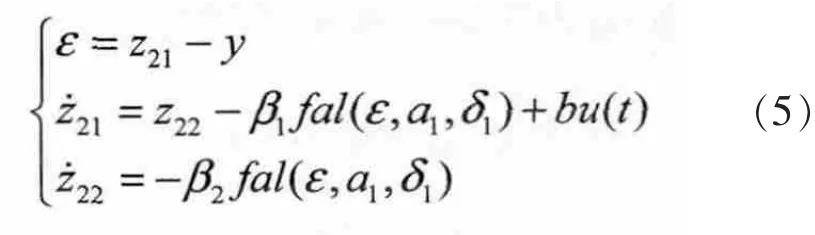
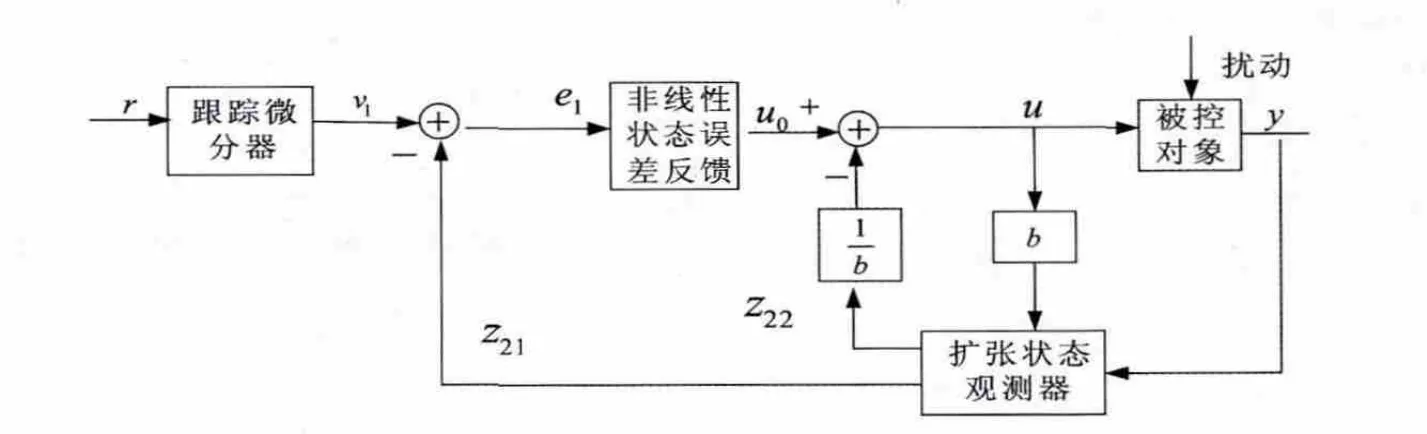
图2 自抗扰控制结构图

非线性状态误差反馈律方程为

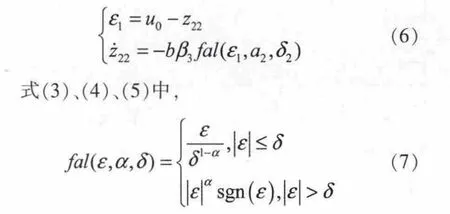
式中：0＜α＜1 常数，α 越小，跟踪越快，但滤波效果越差；δ为影响滤波效果的常数，δ越大，滤波效果越好，但是增加了跟踪的延迟[10]。

z21，z22分别用来跟踪估计状态x和和扰动w(t)，即：

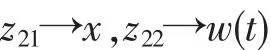
对于一阶被控对象，可以省略TD环节，当扰动容易测量时，可以不采用扩张状态观测器来观测扰动，可以直接对扰动进行测量，这样效果更好[12]。

设光伏并网逆变器稳态运行，由逆变器两侧功率平衡可得在dq坐标下表达式

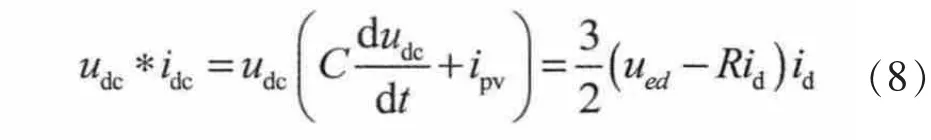
将上式改写为设计自抗扰控制器的规范形式

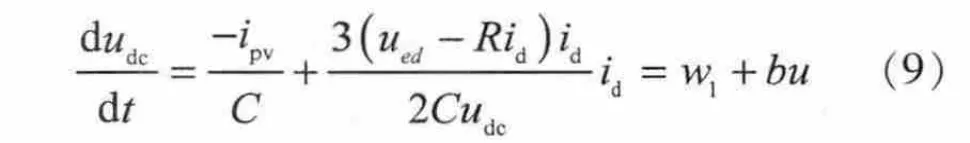
由于为一阶系统，并且可以直接测量电流ipv所产生的扰动，所以省去微分跟踪器和扩张状态观测器。直接得到一阶非线性状态误差控制律为：

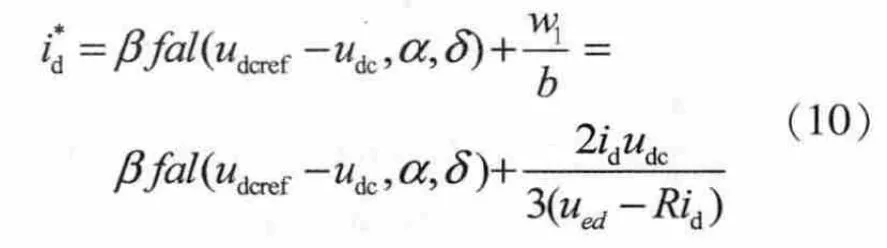
式中udcref为光伏电池最大功率点电压。

2.2 无源控制器及设计

将式（1）写为 EL 形式[13、14]

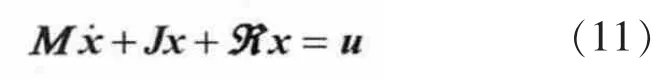
式中：M为正定的对角矩阵；J为反对称矩阵，反映内部的互联结构； 为对称正定矩阵，反映了系统的耗散特性，系统与外部能量交换用u表示。各矩阵具体表达式为：

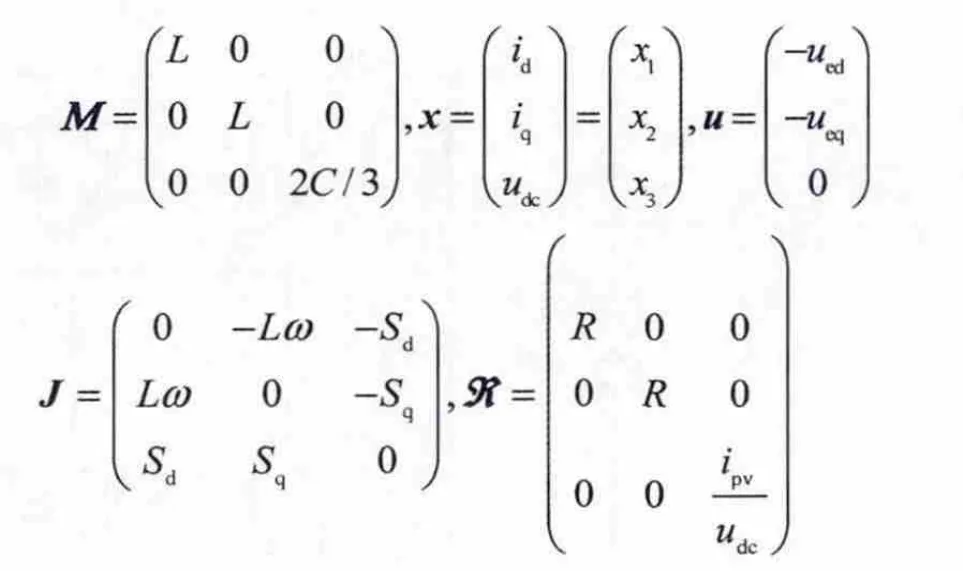
当系统稳态运行时，期望功率因数为1，直流侧电压等于最大功率点输出电压，则期望平衡点为为期望交流侧线电流d轴值）为期望交流侧线电流q轴值），为电容两端的期望电压值）。

选择系统的误差存储函数为

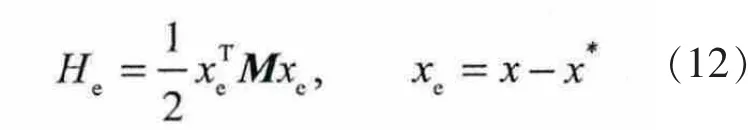
上式中x*为系统的期望平衡点。

为了加速系统的收敛速度给系统加入阻尼，设耗散项为 则将式（11）改写为

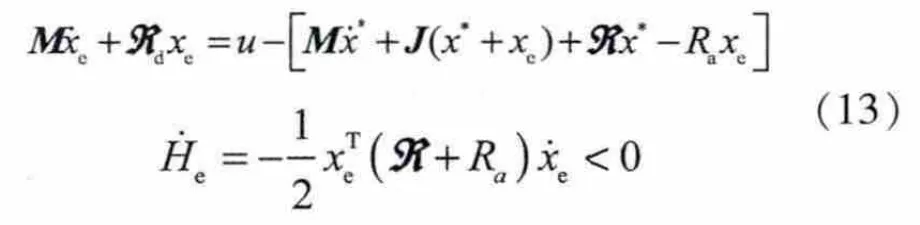
选择控制律

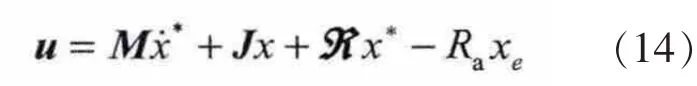
考虑到 =0，可以得到系统的开关函数为

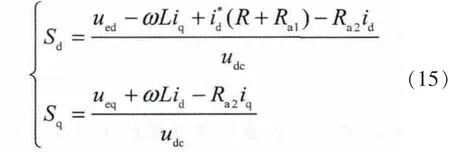
将式（15）代入式（11）可得

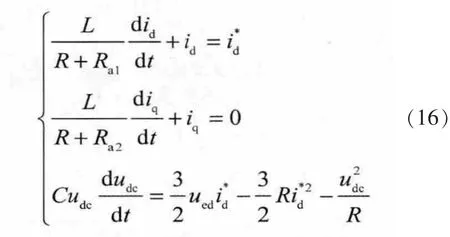
式(16)表明控制律式（15）能够很好的实现系统的动态和静态解耦，提高系统的动静性能。

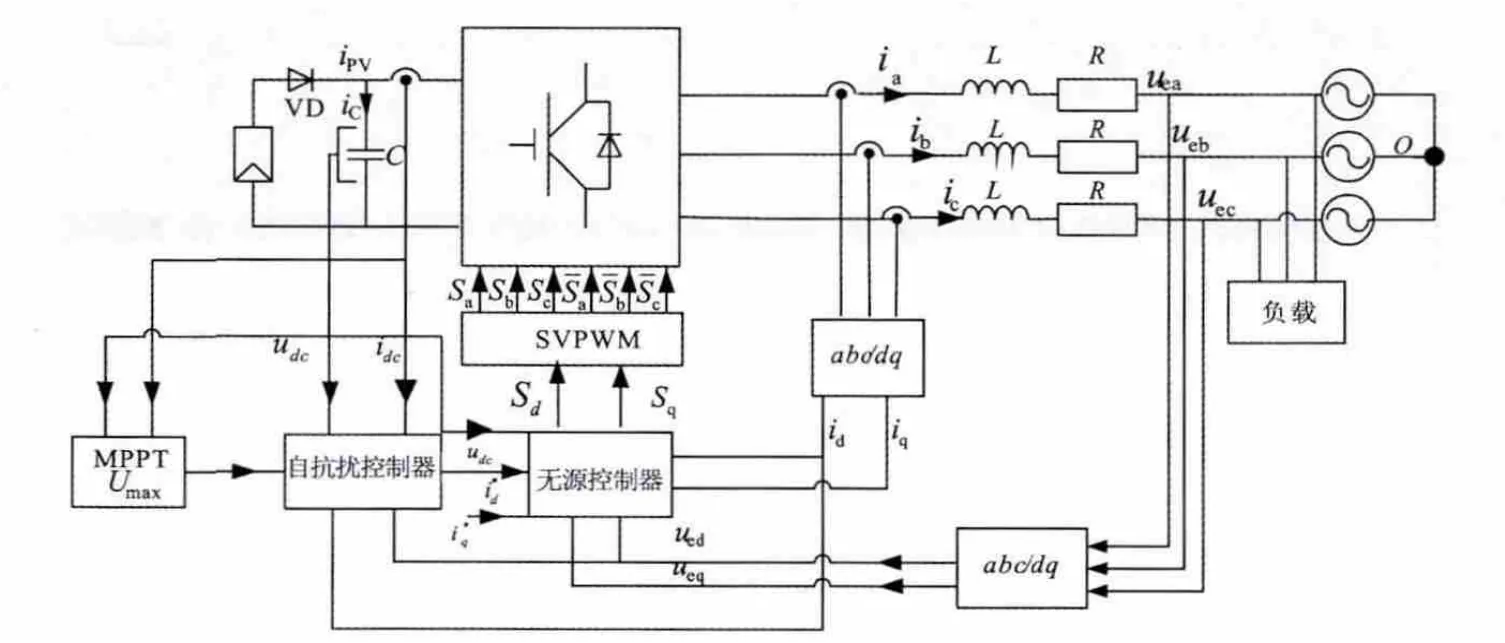
图3 基于自抗扰和无源控制的光伏并网逆变器结构图

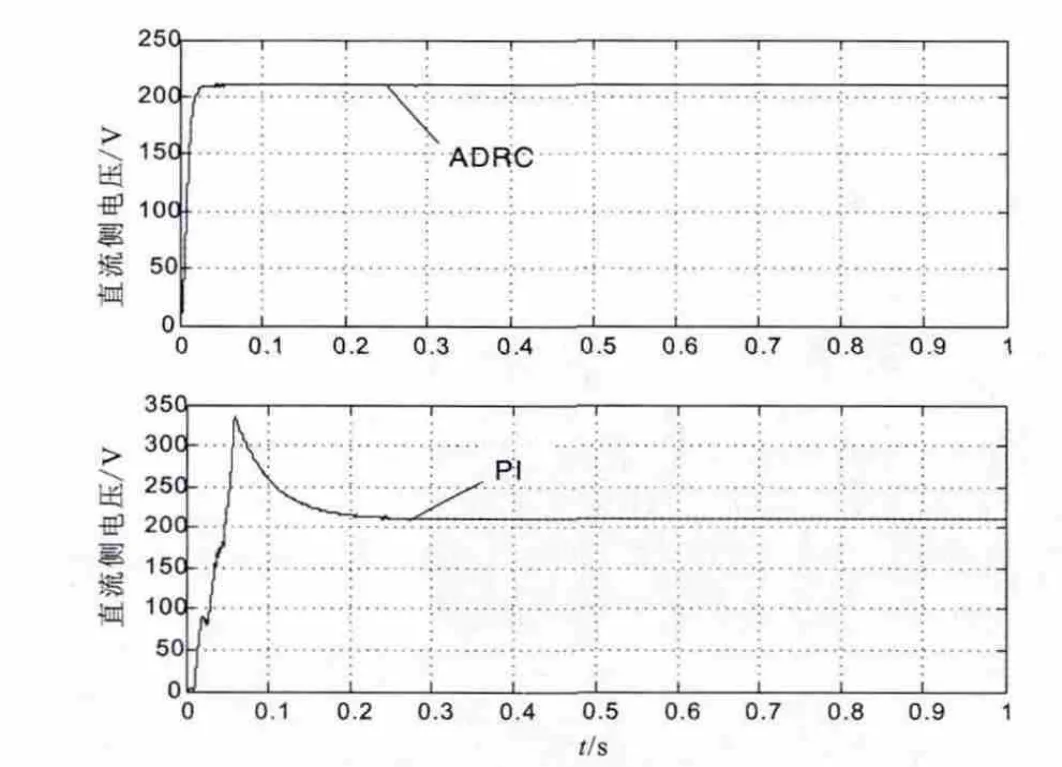
图4 采用ADRC和PI控制的直流侧电压波形

根据以上控制器设计，可以得到基于自抗扰技术和无源控制理论设计的逆变器系统结构如图4所示。

3 实验结果

3.1 系统仿真

使用 Matlab/Simulink软件对图4所示系统进行仿真。其中三相电网平衡相电压峰值为160 V，逆变器输出端电抗器电感为15 μF，电抗器电阻和逆变系统内阻为0.2 Ω，电容器电容为2 200 μF，注入阻尼Ra1、Ra2取为20 Ω。经过自抗扰参数调节规律和多次试验，最终取自抗扰控制器参数β、α、δ值分别为-0.3，0.75，1。

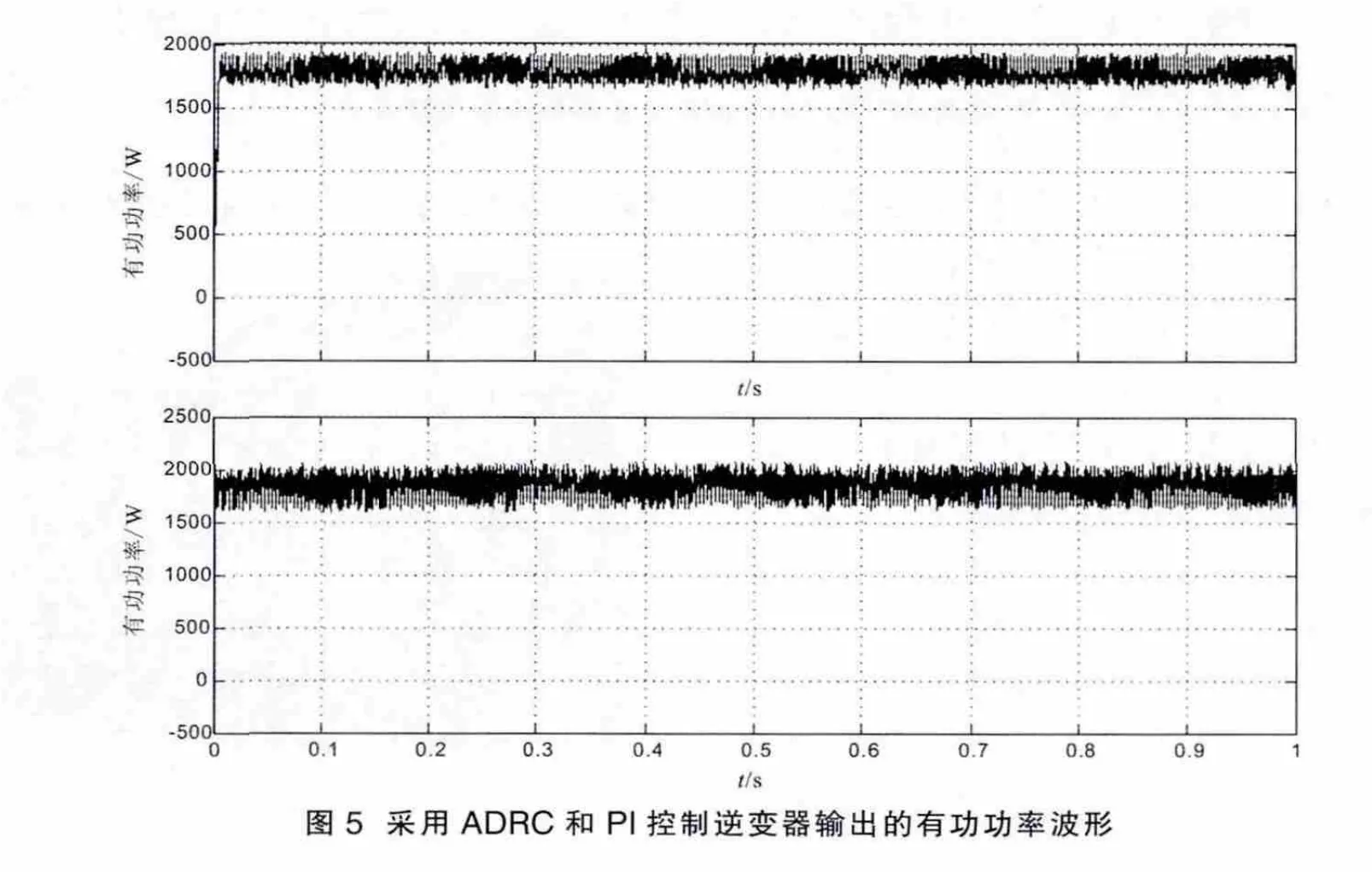
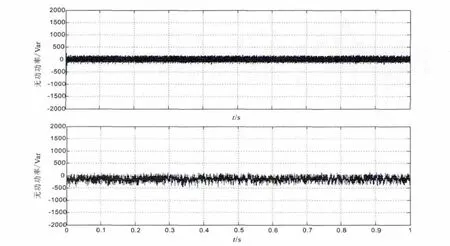
图6 采用ADRC和PI控制逆变器输出的无功功率波形

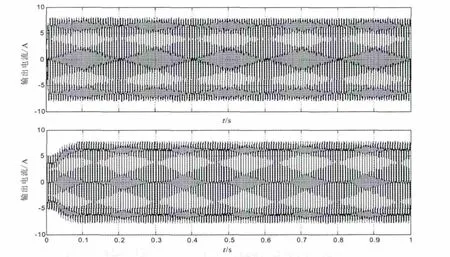
图7 采用ADRC和PI控制逆变器输出端电流波形

图6 为采用ADRC和PI控制的直流侧电压波形图，可比前者电压响应速度更快、无超调、稳态精度更高。图7和图8分别为逆变器输出的有功功率和无功功率波形图，采用ADRC技术的控制策略与采用PI的控制策略相比有功功率没有超调，响应速度更快。图9为逆变器输出端电流波形图，可以看出采用ADRC技术逆变器输出端电流在0.03 s左右实现正弦化并达到稳定，而采用PI控制策略要到0.14 s左右才能实现正弦化并达到稳定。

3.2 实验结果

图8 实验平台

采用为进行光伏并网逆变器实验研究，搭建了微电网 （三相线电压AC 380 V经隔离变压器变为三相线电压 AC 220 V）和 1.2 kV·A的阻感负载、MyWay的电子负载 （可输出直流电压）TMS320F28335（DSP）控制的逆变器等组成实验平台如图8所示。直流电压设置为400 V，电容值为2200F，电抗器电感为10 mH，变压器的电压比为380∶220。动力线电网线电压为 380 V。采用FLUKE434电能质量分析仪，Tektronix TPS2104 100M数字隔离示波器等仪器进行测试。

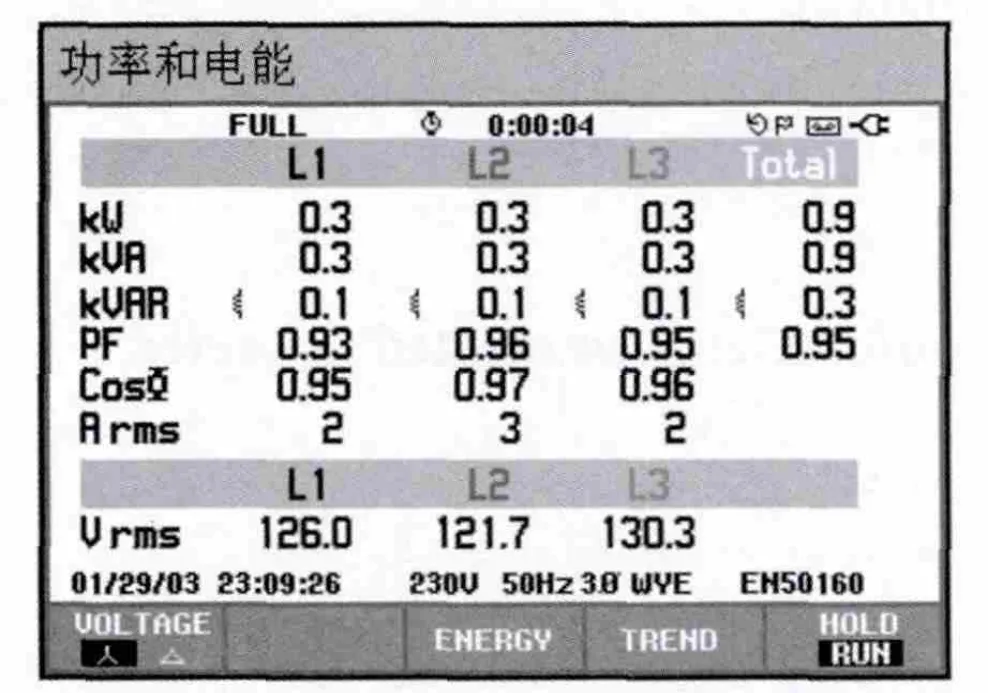
图9 电能功率和电能图

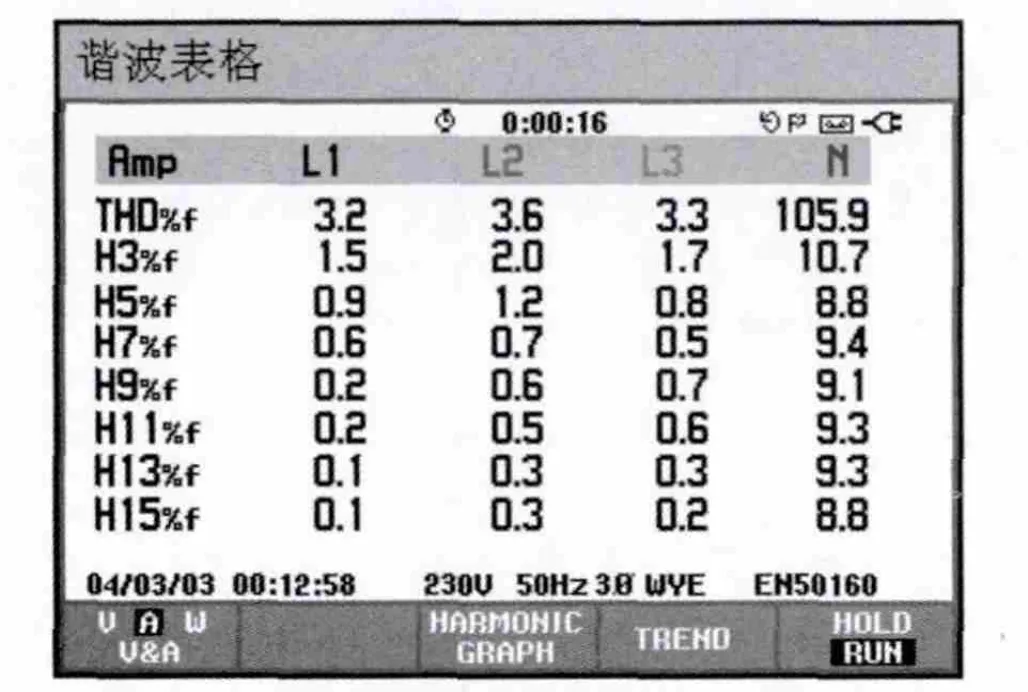
图10 奇次谐波含量图

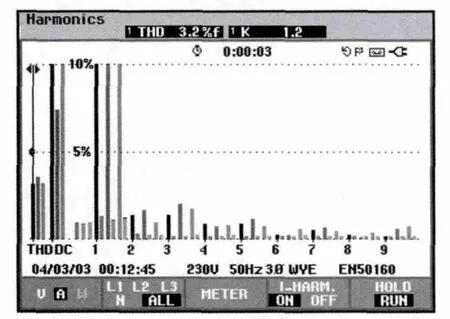
图11 总谐波含量图

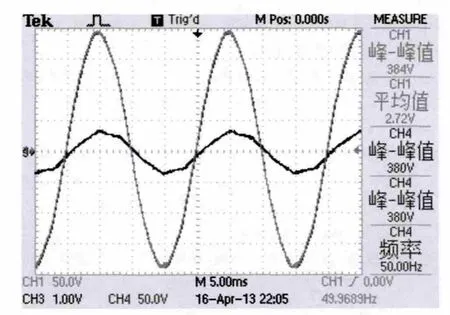
图12 逆变器输出并网电压电流波形

4 结语

在光伏并网系统中，逆变器控制是其中最重要的环节。本文采用自抗扰技术和无源控制理论相结合的控制策略具有直流侧电压稳定、可调参数少、响应速度快等优点。对提高能源转换率以及自抗扰技术和无源控制理论在光伏逆变器中的应用具有一定的指导意义。

[1]张兴，曹仁贤，等.太阳能光伏并网发电及其逆变控制[M].北京：机械工业出版社，2011.

[2]洪巧文，蔡逢煌，戴永辉，王武.光伏发电系统的新型双闭环控制算法研究[J].电源学报，2012（04）：54-58.

[3]李文杰，孙志毅，何秋生.基于模糊自适应 PID的光伏并网双闭环控制[J].工业控制计算机，2012，25(04)：47-48.

[4]徐志英，许爱国，谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J].中国电机工程报，2009，29(27)：36-41.

[5]张淼，刘立强.光伏三相并网系统的自抗扰控制[J].控制理论与应用，2008，25（01）：175-177.

[6]梁芳.基于自抗扰控制技术的并网光伏控制系统[D].天津：天津理工大学，2012.

[7]慕小斌，王久和，顾问，徐升升.基于无源性的光伏并网逆变器非线性电流控制策略[J].电源学报,2011(04)：83-87.

[8]Xiaobin Mu,Jiuhe Wang,Hao Xiang.Study on anonlinear control strategy for three-phase voltagesources PWM DC/AC inverter based on PCHmodel[C].IEEE Conference on Electrical Machines System.

[9]韩京清.自抗扰控制技术-估计补偿不确定性因素的控制技术[M].北京：国防工业出版社,2008.

[10]王久和.先进非线性无源控制理论及其应用[M].北京：科学出版社，2012.

[11]韩京清.非线性状态误差反馈控制律—NLSEF[J].控制与决策，1995，10(03)：221-225.

[12]刘子健，吴敏，等.三相电压型PWM整流器自抗扰控制[J].信息与控制，2011，40(04)：452-458.

[13]王久和.电压型PWM整流器的非线性控制[M].北京：机械工业出版社，2008.

[14]R Ortega,E Garcia-Canseco.Interconnection and damping assignment passivity-based control：a survey[J]JEur.J Control,2004,(11)：432-450.