基于DSPN的航天器系统级可测试性指标确定方法

（北京空间飞行器总体设计部，北京 100094）

1 引言

可测试性是指产品能及时、准确地确定其状态（可工作、不可工作或性能下降）并隔离其内部故障的一种设计特性［1-2］。国外自20世纪90年代起，就充分考虑复杂系统可测试性设计，以提高可靠性和降低成本，其中包括“铱星”系统和F-22 战机的研制。国内相关研究起步较晚，针对系统级指标确定，武器装备领域对基于Petri网和遗传算法的方法进行了研究［1，3］。航天领域的标准明确指出，“要根据产品特点把可测试性设计到产品和设备中去”［4］，并且提出“可测试性定量要求，主要指对故障检测率、故障隔离率、故障检测时间、故障隔离时间和虚警率等指标提出要求”［5］。但目前实际工程中，可测试性工作基本停留在定性要求上，缺乏有效的系统级指标确定和设计手段。作为一种设计指标，可测试性指标需要先确定系统级要求，再进行指标分配及其它环节，这就导致可测试性工作难以开展、可测试性思想难以应用。

本文对基于确定与随机Petri网（Deterministic and Stochastic Petri Nets，DSPN）的可测试性指标确定方法进行研究。可测试性指标要求的输入，来自系统可用度、可靠性、总体优化考虑等系统约束，其输出分级传递，最终体现在系统测试过程中，因此建立输入与输出的关系成为指标要求确定问题的关键［4，6］。DSPN 作为一种系统建模工具，通过对系统状态及状态变化的建模，可以有效覆盖描述系统状态变化过程的各类时间参数和概率参数［7］。因此，对系统测试过程进行DSPN 建模，将可测试性指标及其影响因素联系起来，再对模型进行数学求解，确定所需指标是可行的。该方法可为今后系统级可测试性指标要求的确定提供参考。

2 DSPN 简介

Petri网（Petri Nets，PN）是一种图形化离散动态系统建模工具，以研究模型系统的组织结构和动态行为为目标，在通信协议、计算机组织结构、可靠性分析等方面应用广泛。DSPN 是PN 的扩展，主要体现在将变迁分为瞬时变迁和延时变迁。瞬时变迁的实施时间为零，与随机开关相关联；延时变迁的实施时间既可以是确定常数，也可以是服从指数分布的随机变量，从而可以更充分地描述系统故障、检测、维修等与时间相关的随机事件［7-8］。本文使用的主要DSPN 结构元素见表1，通过变迁的实施，系统状态标识在位置中进行移动，从而遍历系统状态。

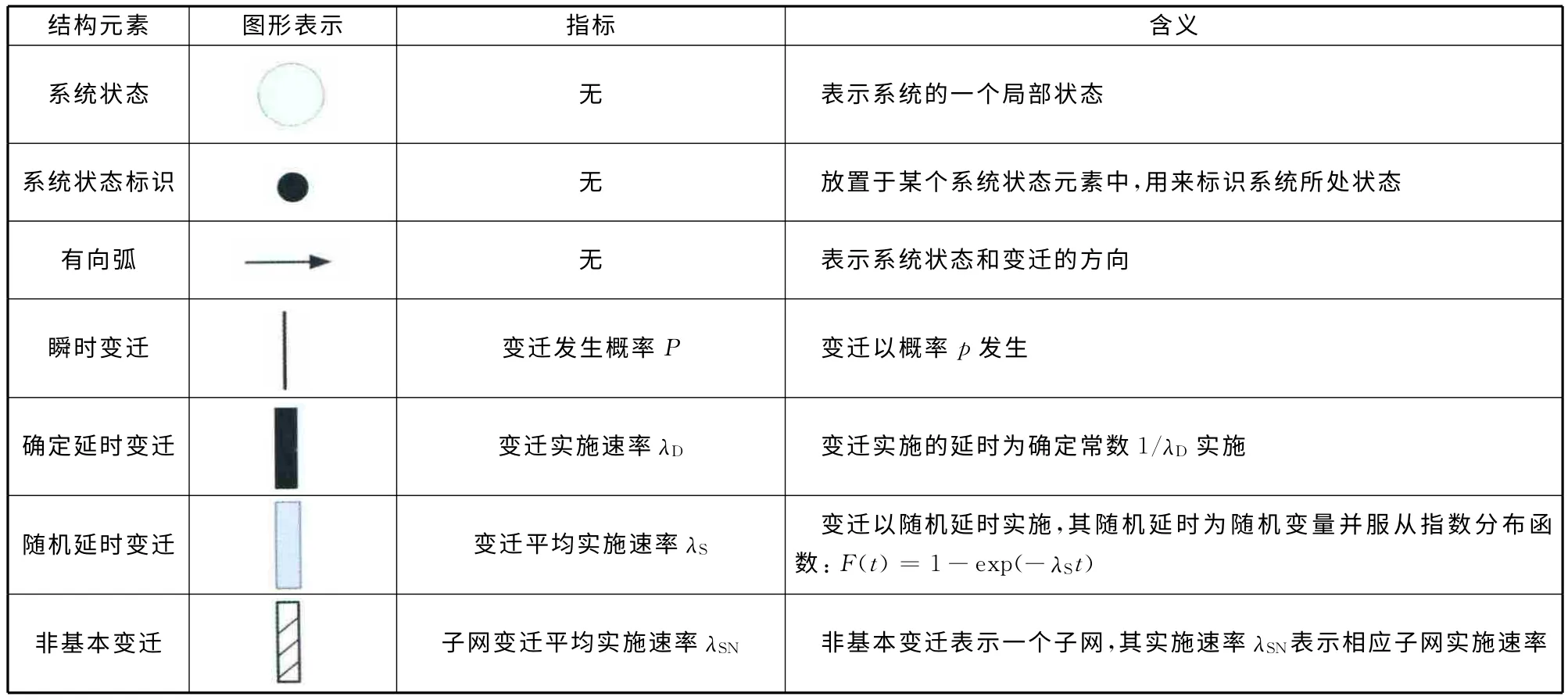
表1 DSPN 结构元素Table 1 Configuration element of DSPN

3 航天器系统测试过程的DSPN模型

3.1 问题分析

航天器可测试性指标主要包括故障检测率、故障隔离率、故障检测时间、故障隔离时间和虚警率，这些指标是模型的未知变量和求解目标。系统级可测试性指标影响因素主要有系统可用度、可靠性指标、系统结构等，还有测试模式、测试环境、测试能力的影响［1-2］，对其假设如下：型号使用可用度要求为A、型号故障率为λ，系统包含有n个分系统，型号测试和故障处理分为系统级和现场可更换单元（Line Replace Unit，LRU）级［1］，系统测试采用连续运行的工作模式，系统测试有虚警率要求。

航天器系统测试与LRU 级（包含在分系统测试中）的测试对象、测试环境、测试接口和可靠性要求不同，二者存在动态过程需求，因此对可测试性指标的要求也不同。以确定可测试性指标为目的对测试过程建模，应充分考虑两个层级的不同输入对分析结果的影响，进行分级建模。根据系统级测试和故障处理过程，系统状态大致可分为5个阶段，如图1所示。

图1 系统测试和故障处理过程Fig.1 Process of system test and failure disposal

系统故障过程包含可靠性指标；故障检测阶段包含故障检测相关指标；故障隔离阶段包含故障隔离相关指标；故障维修阶段包含故障LRU 返厂维修等操作，实际上等同于分系统级故障测试处理过程；另外，还应包含虚警环节和总装、运输等中间环节。

3.2 问题建模

模型依照图1中的过程顺序进行搭建，相应系统故障检测处理过程的DSPN 模型如图2，具体模型说明见表2。结合图2对系统状态变化说明如下。

图2 系统故障检测处理过程DSPN 模型Fig.2 DSPN model of system test and failure disposal process

表2 系统故障检测处理过程DSPN 模型说明Table 2 Annotation of DSPN model of system test and failure disposal process

系统初始由正常状态P1到系统故障P2；故障检测完毕P3后，若故障不可测P4（故障检测率造成）经人工检测才使故障被检测P5，否则故障直接被检测P5；故障隔离完毕P6后，若故障不可隔离P7（故障隔离率造成）经人工隔离才使故障被隔离P8，否则故障直接被隔离P8至单机LRU；对已隔离的n个LRU 经拆卸进入单机返厂维修过程（P9至P18），其中返厂维修过程与系统级检测隔离步骤大致相似；LRU 维修完毕后进行装配，返回系统正常状态P1；对虚警过程，系统虚警PFA后，经虚警故障隔离及人工排查，确定系统虚警返回系统正常状态；并对各状态间变化过程进行了变迁设置。

4 DSPN 模型求解

模型求解思路是将模型转化为与可达图状态相同的的马尔科夫链，然后求解该马尔科夫链。为简化分析，以图2中两级连接点P9和P18为界，设置系统级子网和LRU 级子网，进行简化和替代得到简化LRU 级的系统等效DSPN 模型，如图3所示，对等效DSPN 模型定义系统状态可达标识见表3。在系统级模型中求解出LRU 级等效状态PSS和LRU级平均实施速率TSS的相关参数后，就可以代入被简化子网进行分系统级或LRU 级设计分析，从而方便可测试性指标的传递和分配。

图3 等效DSPN 模型Fig.3 Equivalent DSPN model

表3 等效DSPN 模型状态可达标识表Table 3 State attainability annotation of equivalent DSPN model

为将模型同构于马尔科夫链进行求解，须要消除瞬时变迁的随机开关对系统结构的影响，因此对可达图进行状态压缩，得到状态压缩的DSPN 模型，相应状态可达图见图4。

图4 状态压缩的等效DSPN 模型状态可达图Fig.4 State attainability plot of constringent equivalent DSPN model

图4可同构为一个离散空间连续时间的半马尔科夫过程，相当于在一个连续时间马尔可夫链（CTMC）中，有限个状态的驻留时间变为常量［9-10］。将此CTMC记为随机过程X（t），t≥0。定义其稳态概率（S为系统状态全集），状态转换概率pij（τ）＝P｛X（t＋τ）＝j｜X（t）＝i｝，i，j∈S，i≠j，状态转换速率qij＝得到CTMC状态转换速率矩阵Q：

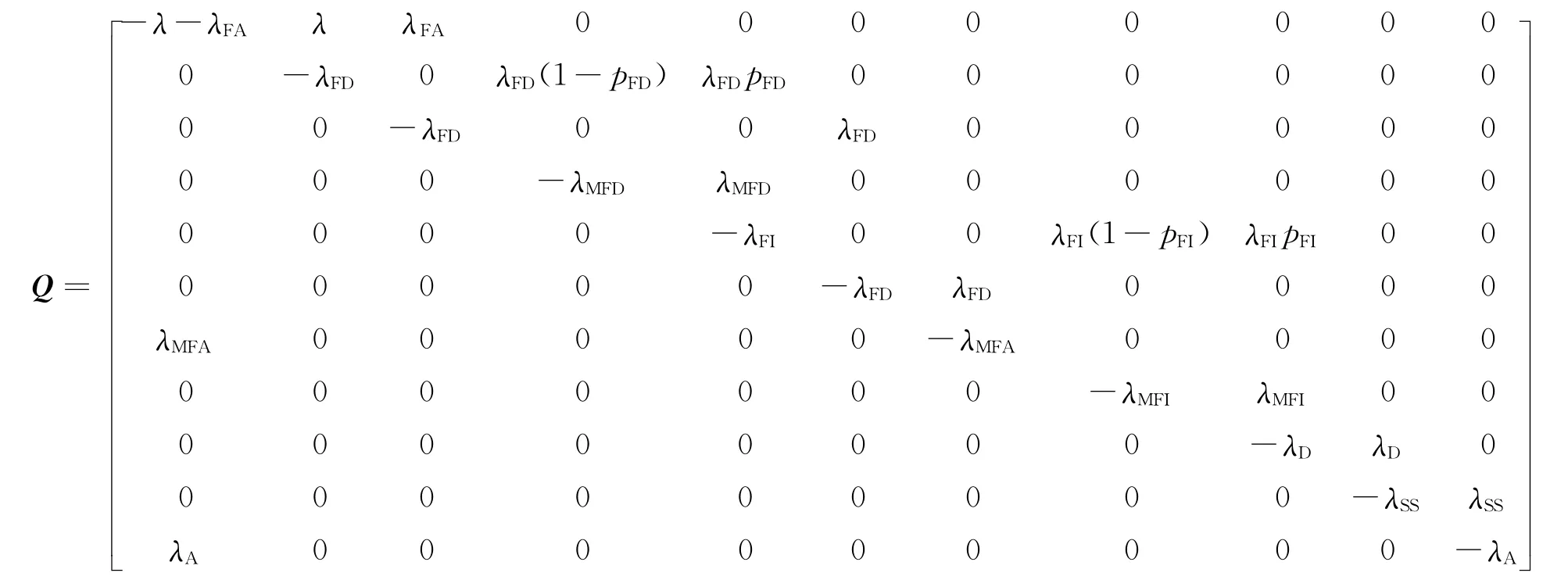
对CTMC时间采样得到嵌入马尔可夫链（Embed Markov Chain，EMC），根据矩阵Q求解EMC，再由CTMC与EMC稳态概率的关系，可解得CTMC稳态概率［6，11］，即航天器系统测试过程DSPN 模型各状态稳态概率。其中系统正常状态M0稳态概率（即系统稳态可用度A0）如下：

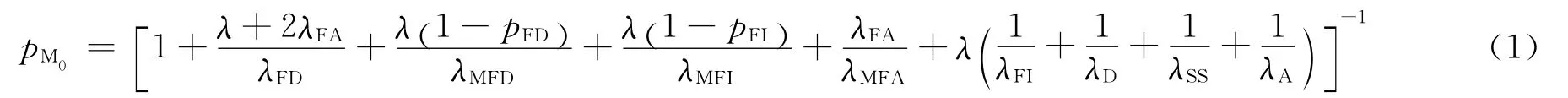
式（1）就是系统可用度与可测试性指标的关系式，即模型求解结果，可对其进行指标分析。

5 指标确定举例

对系统稳态可用度、系统可靠度等目前已有的已知指标，其取值尽量贴近工程值；对故障检测和隔离相关的速率等尚不明确的已知指标，结合工程经验进行假设；待求指标为标准中规定的5 项指标以及LRU 级平均实施速率；综上整合指标信息见表4。

表4 已知指标及待求指标Table 4 Index default and unknown quantity

根据可靠度函数R（t）＝1-e-λt，得到故障率λ≈1.944×10-5h-1。参数带入式（1），可得

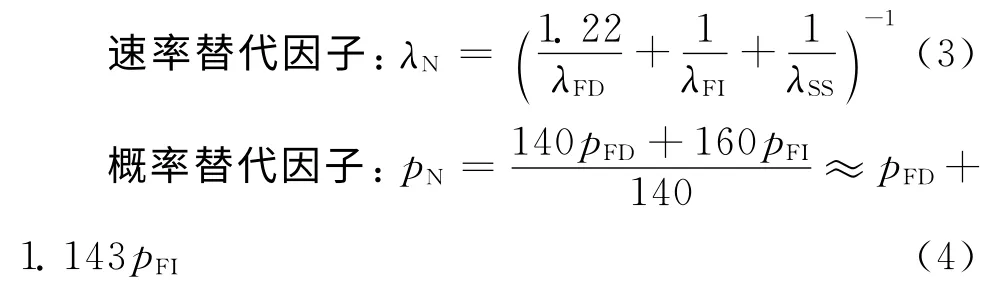
对于λN，假设pN中pFD、pFI均是在［0.6，1］范围内的概率值，由式（4）得到pN∈［1.3，2.2］，因此，在该区间内对pN平均间隔取值作为参量，作λN与稳态可用度关系如图5（a）。系统稳态可用度要求不小于0.98，则应有λN≥0.004h-1；而λN≤0.007h-1以后，提高λN对提高系统稳态可用度带来的收益明显变低，因此限定λN范围［0.004，0.007］。另外假设考虑成本约束，要求系统稳态可用度在0.985以内，则易见pN取1.9附近值 时，曲线较为合适。

对于pN，选取λN在［0.004，0.007］内平均间隔取值作为参量，作pN与稳态可用度关系如图5（b）。选取pN＝1.9附近的区间［1.7，2］，在其内观察曲线，系统稳态可用度范围同样定为［0.98，0.985］，可见λN≥0.005h-1时，曲线较为合适。

综上，为使设计成本最小，在满足系统要求的可适范围内，取λN最低值λN＝0.005h-1，以及此时pN最低可适值pN＝1.9。

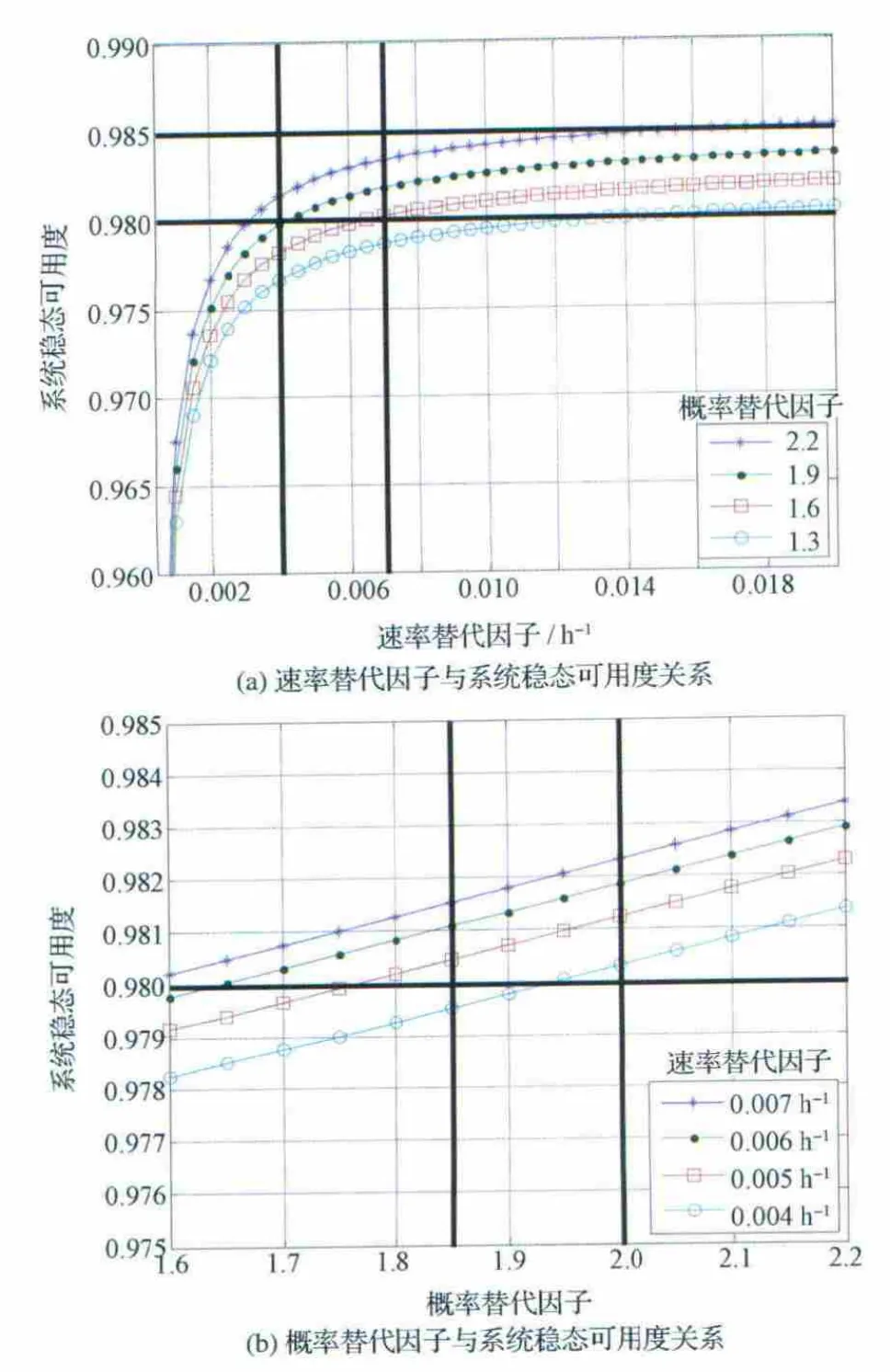
图5 速率替代因子和概率替代因子与系统稳态可用度关系图Fig.5 Relation plot of velocity substitutive factor ＆probability substitutive factor and system usability

这时，已经可以综合设计可测试性指标。本文考虑保证测试覆盖性，对pFD取值尽量高，因此取pFD＝95%；考虑降低技术实现难度，pFI可以偏低，由关系式得到pFI＝83.1%；并且预留更多故障隔离时间；假设分系统测试和故障处理需≥100h，得到指标见表5。其中，虚警率由其它指标代入式（2），结合可用度要求得出，满足系统虚警率≤10%假设，取值得到验证。

表5 系统级可测试性指标结果Table 5 Results of system testability index

6 结束语

针对航天领域系统级可测试性指标确定方法的不足，研究了一种基于DSPN 的航天器系统级可测试性指标确定方法，通过对系统测试过程的分析和DSPN 建模，以及对该模型的数学求解，确定了故障检测率、故障隔离率、故障检测时间、故障隔离时间、虚警率等可测试性指标与系统可用度、可靠性等约束之间的关系，并通过实例给出了上述指标的分析求解过程。在整个建模分析过程中，各项假设条件可参照实际情况进一步细化，使模型更加贴近实际；另外对系统可用度多元函数的分析还可以进一步研究，以提高指标分析的准确度。从而，可对航天器系统级可测试性指标的设计提供参考。

（References）

［1］邱静，刘冠军，杨鹏，等.装备测试性建模与设计技术［M］.北京：科学出版社，2012 Qiu Jing，Liu Guanjun，Yang Peng，et al.Equipment testability modeling and design techniques［M］.Beijing：Science Press，2012（in Chinese）

［2］石君友.测试性设计分析与验证［M］.北京：国防工业出版社，2011 Shi Junyou.Testability design analysis and verification［M］.Beijing：National Defense Industry Press，2011（in Chinese）

［3］吕晓明，黄考利，连光耀，等.复杂装备系统级测试性指标确定方法研究［J］.计算机测量与控制，2008，16（3）：357-359，362 Lv Xiaoming，Huang Kaoli，Lian Guangyao，et al.Research on deciding testability figures of complicated equipment［J］.Computer Measurement ＆ Control，2008，16（3）：357-359，362（in Chinese）

［4］中国航天工业总公司.QJ3051-98.航天产品测试性设计准则［S］.北京：中国标准出版社，1998 China Aerospace Industry Corporation.QJ3051-98.Testability design standard for spacecraft［S］.Beijing：Standard Press of China，1998（in Chinese）

［5］国防科学技术工业委员会.GJB2547A-95.装备测试性大纲［S］.北京：中国标准出版社，1995 Commission of Science，Technology and Industry for National Defense.GJB2547A-95.Testability program for material［S］.Beijing：Standard Press of China，1995（in Chinese）

［6］David M B，Brain A K，Alony H.Automated testability decision tool［R］.New York：Rome Laboratory Air Force Systems Command Griffiss AFB，1991

［7］林闯.随机Petri网和系统性能评价［M］.北京：清华大学出版社，2005 Lin Chuang.Stochastic Petri nets and system performance evaluation［M］.Beijing：Tsinghua University Press，2005（in Chinese）

［8］李建楠，胡健生，吴文.基于确定与随机Petri网的CSMA／CD 协议建模与分析［J］.计算机应用与软件，2012，29（7）：207-209，253 Li Jiannan，Hu Jiansheng，Wo Wen.DSPN-based CSMA／CD protocol modeling and analysis［J］.Computer Application and Software，2012，29（7）：207-209，253（in Chinese）

［9］Tavana M，Bush T E，Davis E L.Modeling operational robustness and resiliency with high-level Petri nets，AFRL-RI-RS-TP-2012-17［R］.New York：Air Force Research Laboratory，2012

［10］林闯，李雅娟，刘雪宁.非马尔可夫随机Petri网的分析方法及应用［J］.系统仿真学报，2003，15：71-75 Lin Chuang.，Li Yajuan，Liu Xuening.Analysis methods and applications of non-markovian stochastic Petri nets［J］.Journal of System Simulation，2003，15：71-75（in Chinese）

［11］Zijal R，Ciardo G.Discrete deterministic and stochastic Petri nets，ICASE Report No.96-72［R］.Hampton：NASA Langley Research Center，1996