基于变结构控制的反鱼雷鱼雷拦截弹道建模与仿真
2013-12-26张西勇李宗吉王树宗
张西勇,李宗吉,王树宗
(海军工程大学 兵器工程系,武汉430033)
现代海战中,鱼雷由于具备隐蔽性和不易拦截,成为舰艇面临的主要威胁之一。随着科学技术的发展,鱼雷武器正朝着精确制导、智能化方向发展,对舰艇以及潜艇构成的威胁越来越大。鉴于此,世界各国投入巨资开展反鱼雷武器的研究,其中以硬杀伤的反鱼雷鱼雷(ATT)成为研究的热点,而我国的ATT还处于起步研究阶段。ATT也是一种鱼雷,其工作原理和普通鱼雷基本一致,不同的是ATT攻击的目标是鱼雷,而不是舰艇。相比之下,ATT所攻击目标的速度快、机动性强、尺寸小,这样就增加了拦截难度。现有鱼雷中常用的导引律有比例导引法、尾流导引法。比例导引法建立在精确的数学模型基础上,因此鲁棒性差,目标作快速机动时系统响应慢,不适合拦截鱼雷这种小而且机动性强的目标;尾流导引法只适合拦截水面舰艇这种大型目标。文献[1]应用滑模变结构控制技术设计了空空导弹末端拦截导引律,通过设计导弹法向加速度的变结构控制量,达到精确命中目标的目的,而鱼雷的法向加速度无法控制,所以不适合于ATT。文献[2]应用变结构控制设计了反鱼雷武器导引律,控制量复杂,所需参数多,不易工程实现,且导引律的稳定性推导过程存在错误。本文采用变结构控制对ATT的导引律进行了设计,并建立了拦截目标弹道的数学模型。
1 导引律设计
变结构滑模控制由于具有对模型参数变化不敏感、鲁棒性强等特点,越来越广泛地应用于精确武器的制导规律中。如在空空导弹的末端导引中采用变结构滑模控制律后,所需法向过载大大减少,同时脱靶量减小,因而大幅度提高了命中精度。目标和ATT之间的视线角以及目标和ATT的航向角通过声纳装置很容易确定,本文通过ATT和目标之间的运动关系数学模型,建立了基于航向角变结构控制的ATT导引律控制模型。
以平面内情况为例,ATT-鱼雷相对运动关系如图1所示。
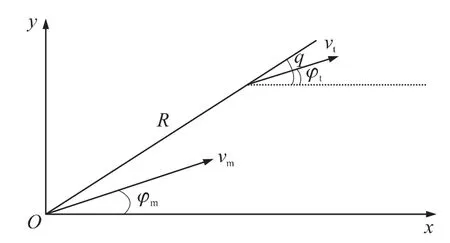
图1 平面内ATT-鱼雷相对运动关系
由图1可以导出如下关系式:
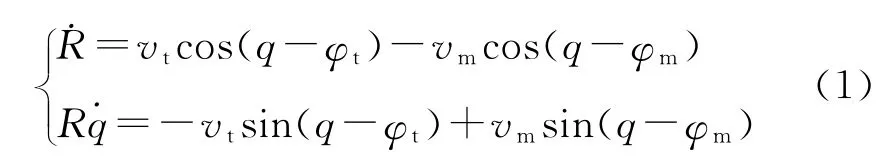
式中:R为ATT与鱼雷之间的相对距离;vt,vm分别为目标速率和ATT速率;q为视线角;φt,φm分别为目标和ATT的速度方向角。
为便于推导,令VR=,Vq=,把它们代入式(1),并对式(1)关于时间求一阶导数,得到:
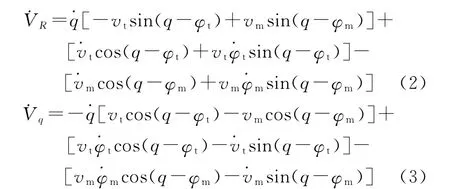
令:
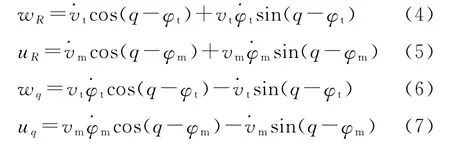
将式(4)~ 式 (7)代入式 (2)和 式 (3),并 注 意到式(1),得到:

将VR=,Vq=代入式(9),得到:

设计制导律的关键在于如何通过uq控制视线角速度,令其趋于0。从而实现准平行接近。取x1=q,x2=,则式(10)可用如下状态方程描述[3-4]:
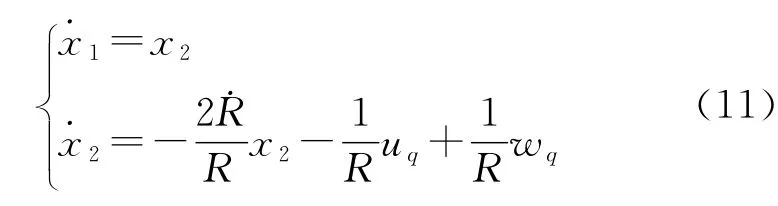
式中:uq为控制量,wq为干扰量。
基于准平行接近原理,选取切换平面为

根据式(11),构造滑模趋近律:
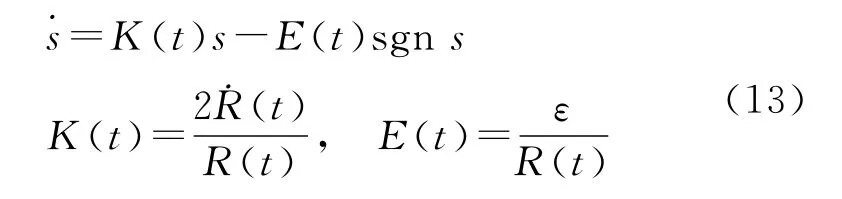
式中:ε为大于0的常数。
将式(12)、式(11)代入式(13)得到滑模制导律:

下面证明在目标鱼雷机动时滑模制导律可以保证x2→0。由 Lyapunov第二法[5-6],选取 Lyapunov函数V=/2。考虑目标机动情况,将式(11)写作:
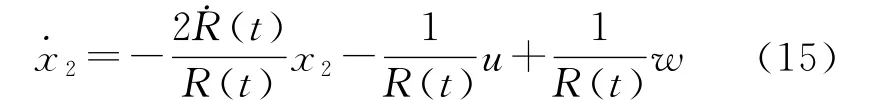
式中:u=uq,w=wq。
将V相对于时间微分得到:
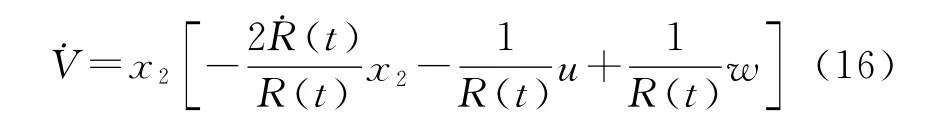
将式(14)代入式(16),得到:

由于有R>0,<0,式(17)中第一项小于0;只要满足ε>|w|,第二项也为负。这样<0成立。
由式(14)知控制量uq存在高速切换,又由式(7)知,在物理上,uq很难实现高速切换。因此,滑模制导律uq=-+εsgnx2在工程上难以实现。采用连续函数代替切换函数的方法实现制导律[7-8],即式中:δ为一很小的正常数。
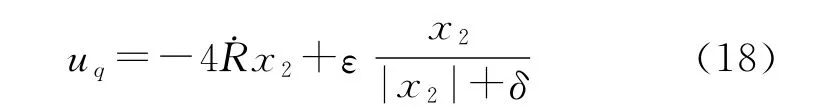
同样,取Lyapunov函数V=/2,得到:

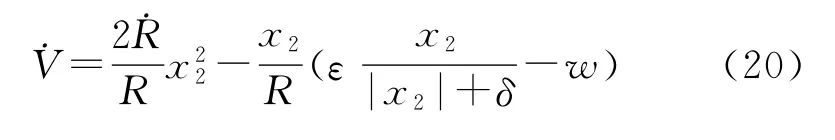
1)目标鱼雷不作机动。
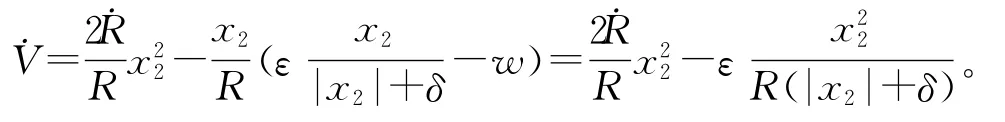
因为有R>0,<0以及ε和δ均为正常数,所以<0,即在目标不作机动时,控制律uq=-能够保证视线角速度趋于0,即命中目标。
2)目标鱼雷作机动。
由式(20)知,当wq≠0时,显然不满足<0,只有当时满足<0,令|w|max为|w|的最大值,则有,即时满足<0。因此,当目标鱼雷机动时,控制律uq=-只能将视线角速度x2稳定地控制在的邻域内,而不能保证x2趋于0。理论上,ATT和目标的视线角稳定控制在一定范围是能够保证ATT精确命中目标的。
2 弹道数学模型
由前面导引律模型和ATT与目标的运动关系,可以建立ATT拦截目标鱼雷的弹道计算模型:

仿真中,假设目标鱼雷以20m/s的速度航行,初始航向角为240°,ATT的速度为30m/s,初始航向角为45°,ATT和目标鱼雷的初始距离为500m,初始视线角为45°,取ε=50,δ=0.01。
3 仿真分析
采用龙格库塔法,对式(21)进行仿真分析,步长取ts=0.001s。
1)目标鱼雷航向恒定。仿真结果如图2~图8所示。

图2 目标鱼雷航向恒定时ATT和目标鱼雷视线角
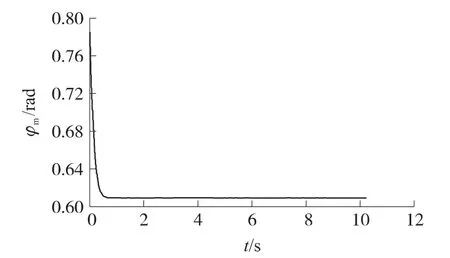
图3 目标鱼雷航向恒定时ATT航向角

图4 目标鱼雷航向恒定时控制量uq的曲线图
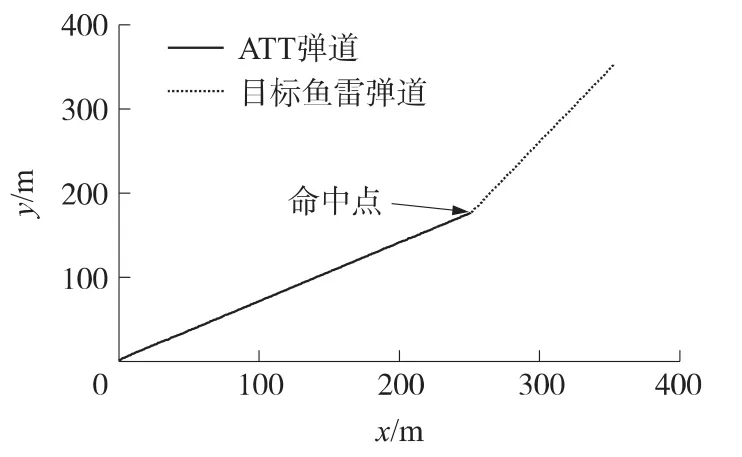
图5 目标鱼雷航向恒定时ATT拦截弹道
仿真时间为12s。仿真结果表明,系统进入滑模状态的时间极短,为0.025s,说明系统响应时间极短,ATT与目标鱼雷视线角稳定控制在一恒定值,验证了前面的理论推导。在10.2sATT准确命中目标,ATT弹道成一条直线,表明目标作直线航行时,ATT法向过载为0,ATT不需作机动就能命中目标。
2)目标鱼雷作蛇形机动。仿真结果如图6~图9所示。
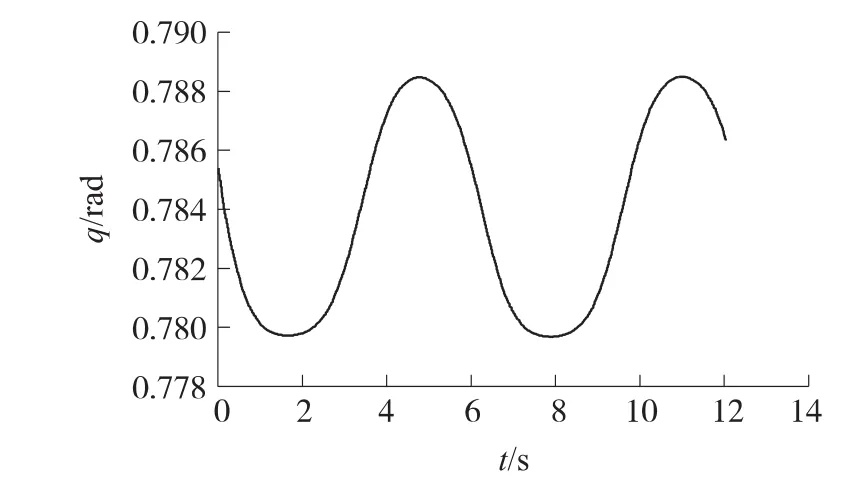
图6 目标鱼雷作蛇形机动时ATT和目标鱼雷视线角

图7 目标鱼雷作蛇形机动时ATT航向角

图8 目标鱼雷作蛇形机动时控制量uq的曲线图
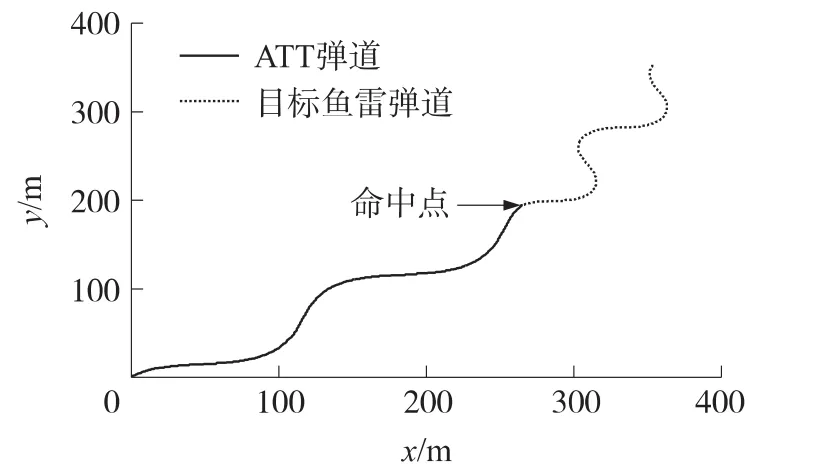
图9 目标鱼雷作蛇形机动时ATT拦截弹道
仿真时间为14s。仿真结果表明,系统进入滑模状态的时间短,为0.788s,这表明系统响应时间短,ATT与目标鱼雷视线角稳定控制在一恒定值的小邻域内,与理论推导相吻合。在12sATT准确命中目标,ATT弹道平滑,法向过载小。
3)目标鱼雷作大角度机动。仿真结果如图10所示。
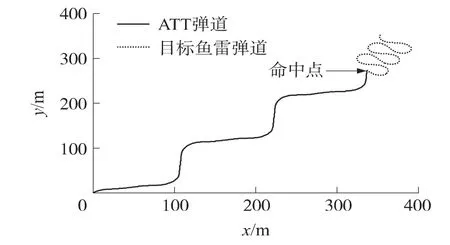
图10 目标鱼雷作大角度机动时ATT拦截弹道
由图2和图6可以看出,在控制律uq=-42的作用下,ATT和目标鱼雷的视线角很快稳定在一固定值的小范围内,满足平行接近原理。由图5、图9和图10可以看出,ATT直接命中目标,弹道稳定平滑,ATT法向过载小;当目标直线航行时,ATT弹道是一条直线,不存在法向过载;当目标作蛇形机动时,ATT也能精确命中目标,并且弹道平滑,法向过载小,系统响应快。当目标作直线运动时系统的响应时间几乎为0,目标作机动时响应时间也不到1s。实际上,由于变结构控制的强鲁棒性,导引律对模型参数测量误差及外界干扰具有强鲁棒性。
4 结论
本文设计了基于变结构的反鱼雷鱼雷导引律。导引律通过控制ATT的航向角来导向目标鱼雷,并在理论上证明该导引律能够使ATT稳定地以准平行接近方式导向目标鱼雷,并对目标鱼雷的机动具有鲁棒性。在导引律的基础上,建立了ATT拦截弹道的仿真模型,并对弹道进行了仿真计算,从仿真结果可以看出,ATT具有非常高的命中精度,能够直接碰撞目标,在目标作蛇形机动时,ATT也能保证命中目标,并且弹道平滑,法向过载小,系统响应快,表明本文所设计的导引律适于在反鱼雷鱼雷中应用。
[1]王湛,贾晓洪,阎杰.空空弹道末端控制滑模导引律研究[J].航空兵器,2005,30(2):3-6.WANG Zhan,JIA Xiao-hong,YAN Jie.Study on the endgame sliding-mode guidance law of air-to-air missile[J].Aero Weaponry,2005,30(2):3-6.(in Chinese)
[2]刘宇.基于变结构控制的反鱼雷武器导引律[J].火力与指挥控制,2010,25(10):87-90.LIU Yu.Anti-torpedo weapon guidance law based on variable structure control[J].Fire Control and Command Control,2010,25(10):87-90.(in Chinese)
[3]高为炳.变结构控制理论基础[M].北京:中国科学技术出版社,1990.GAO Wei-bing.Theory of variable structure control[M].Beijing:China Science and Technology Press,1990.(in Chinese)
[4]禹春来,许化龙,刘云峰,等.导弹姿态控制系统快速输出采样离散变结构自适应控制[J].弹箭与制导学报,2008,10(4):77-80.YU Chun-lai,XU Hua-long,LIU Yun-feng,et al.Discrete variable structure control for missile attitude control with fast output sampling feedback and adaptive control[J].Journal of Pro-jectiles,Rockets,Missiles and Guidance,2008,10(4):77-80.(in Chinese)
[5]高磊,徐德民,任章.被动式鱼雷的自适应变结构制导律设计[J].兵工学报,2001,19(5):280-283.GAO Lei,XU De-min,REN Zhang.Adaptive variable structure guidance law for passive torpedo[J].Acta Armamentarii,2001,19(5):280-283.(in Chinese)
[6]詹致祥.鱼雷制导规律及命中精度.西安:西北工业大学出版社,1995:116-232.ZHAN Zhi-xiang.Guidance law and hitting precision for torpedo[M].Xi′an:Northwestern Polytechnical University Press,1995:116-232.(in Chinese)
[7]陈晔,赵兴堂,王德石.鱼雷深度弹道的自适应反演鲁棒控制[J].弹道学报,2009,21(3):82-85.CHEN Ye,ZHAO Xing-tang,WANG De-shi.Robust adaptive backstepping control for depth ballistics of torped[J].Journal of Ballistics,2009,21(3):82-85.(in Chinese)
[8]孙未蒙,张靖男,刘湘洪,等.一种新的变结构模型参考自适应制导律[J].弹道学报,2010,22(2):5-9.SUN Wei-meng,ZHANG Jing-nan,LIU Xiang-hong,et al.A model-reference adaptive variable structure guidance law[J].Journal of Ballistics,2010,22(2):5-9.(in Chinese)
