一维射影变换及其性质

王 燕

王燕/镇江高等职业技术学校中学一级教师（江苏镇江212000）。

公元前200年左右，古希腊数学家阿波罗尼奥斯在《圆锥曲线论》中把二次曲线作为正圆锥面的截线来研究。公元4世纪，帕波斯在《数学汇编》中记载了射影几何学的一些基本概念，如对合、非调和比（即交比）等，还得到“帕波斯定理”。文艺复兴时期，意大利数学家阿尔贝蒂于1435年发表《论绘画》一书，阐述了最早的数学透视法思想，他引入投影线和截景概念，提出在同一投影线下和景物的情况下，任意两个截景间有何种数学关系或何种共同的数学性质等问题，这些问题是射影几何发展的起点。意大利学者、艺术巨匠达·芬奇 （1452－1519）在《绘画专论》（1651年出版）中坚信，数学的透视法可以将实物精确地体现在一幅画中，它是绘画的舵轮和准绳。意大利另一位画家、数学家弗兰切斯卡约于1478年著有《透视画法论》，推进了阿尔贝蒂的投影线和截景的思想，把透视法的数学原理以相当完整的形式表述出来。

17世纪数学家们重新研究古希腊的圆锥面截线问题和文艺复兴时期的透视法原理，积累了射影几何的原始素材，同时开始进行系统的综合整理工作。1604年德国天文学家、数学家开普勒在 《天文学的光学部分》中提出平行线的无穷远点概念。1636——1639年法国数学家德扎格先后出版《论透视截线》的小册子和《圆锥曲线论稿》。德扎格论述了“德扎格定理”，即如果两个三角形对应顶点的连线共点，则它们对应边的交点共线，反之亦然，这已成为射影几何学的基本定理。法国数学家彭色列在复兴射影几何方面做出了杰出贡献，他构思的巨著《论图形的射影性质》是几何学上的一个里程碑，给射影几何的研究以巨大的动力，开创了射影几何史上的黄金时代。同时以彭色列为首的一大批几何学家的共同努力，迎来了19世纪射影几何蓬勃发展的春天。射影几何以其直观优美、宏伟深刻的新姿独领风骚，一朵颓萎了200多年的蓓蕾终于开出了艳丽之花！

一、透视对应(中心射影)

定义1.1以下三种对应称为一维基本形的透视对应

推论1.1

(1)透视对应是两个一维基本形之间的一个一一对应,保持任意四对对应元素的交比不变.

(2)连续两次透视对应的结果显然不一定仍是透视对应 .透视对应不满足“传递性”，所以透视对应不是一维基本形之间的等价关系.

二、一维射影对应的综合法定义

1.Poncelet定义

设[π],[π']为两个一维基本形.若存在n个一维基本形

[πi](i=1,2,…,n), 使得

则称由此决定的[π]到[π']的一一对应为一个射影对应,记作

推论2.1

（1）透视对应是射影对应，反之不一定成立.

（2）射影对应是一维基本形集合上的一个等价关系.

（3）射影对应是双射，且保持任意四对对应元素的交比不变.

2.Steiner定义

如果两个一维基本形之间的一个对应φ:[π]-〉[π']满足

(1)φ为一个双射；

(2)φ使得任意四对对应元素的交比相等；

则称 φ 为[π]到[π']的一个射影对应,记作[π]∧=[π']

定理2.1

Poncelet定义⇔Steiner定义.

定理2.2

两个一维基本形间的射影对应可由已知相异的三双对应元素唯一确定.

三、射影对应成为透视对应的条件

定理3.1

两个同类的一维基本形之间的射影对应成为透视对应⇔公共元素自对应.

定理3.2(Pappus定理)

在共面的相异二直线li上各取相异三点Ai,Bi,Ci(i=1,2).设

B1C2×B2C1=L

C1A2×C2A1=M，则 L，M，N 三点共线.

A1B2×A2B1=N

四、射影对应的代数定义

定义4.1

设在两个点列上各取定齐次坐标系.称由非奇异线性对应

决定的两点列间的对应为射影对应.其中(x1,x2)与(x1',x2')为任一对对应点的齐次坐标,ρ为非零比例常数.

定理4.1

代数定义⇔Steiner定义.

五、一维射影变换

1.定义5.1

两个重叠的一维基本形之间的射影对应称为一维射影变换.

2.代数表示

(1)坐标表示

设φ称为一维基本形[π]上的一个射影变换，(x1,x2)与(x1',x2')为任一对对应点的齐次坐标.则

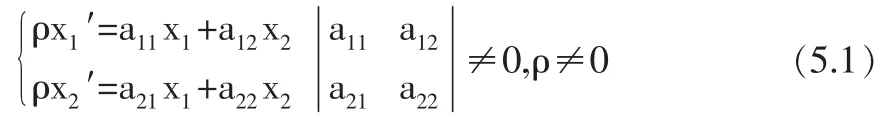
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.

(2)参数表示

定义 形如 axx′+bx+cx′+d=0 (ad-bc≠0)的方程称为关于x,x'的双线性方程.

定理5.1

一维基本形上的一个变换为射影变换⇔其对应元素的参数λ,λ'满足一个双线性方程

3.一维射影变换的分类

设有射影变换

若存在 λ0∈,使 aλ20+(b+c)λ0+d=0,则称 A+λ0B 为 φ 的一个不变元素.

定理5.2

在实复射影平面上,任一个一维射影变换至少有一个不变元素.非恒同的一维射影变换至多有两个相异的不变元素.证明.在(2.13)中,令λ=λ'.则有一维射影变换的不变元方程

立刻可得结论.据此可得一维射影变换的分类：

(1)双曲型、椭圆型射影变换

定理5.3

对于双曲、椭圆型射影变换,任一对相异的对应元素与两个不变元素的交比为常数.称此为射影变换的特征不变量.

证明.设X,Y为两个不变元,P≠P'为任一对相异的对应元.设X,Y,P,P'的坐标依次为x,y,x+y,x+μy.则这四点的参数依次为0,∞,1,μ.于是

(2)抛物型射影变换

定理5.4

抛物型射影变换的不变元参数α与任一对相异的对应元素的参数λ,λ'满足

[1]方德植,陈奕培.射影几何[M].北京：高等教育出版社，1983

[2]周兴和.高等几何[M].北京：科学出版社，2003