配电网可靠性评估贝叶斯网络区间算法

刘禹良，郭剑峰，邹 燕

(1.重庆电力高等专科学校，重庆400053;2.四川省电力公司内江电业局，四川内江641000)

0 引言

国内外已在配电网可靠性评估方面取得较大进展，常用的方法是故障模式后果分析法(FMEA，Failure mode and effect analysis)［1］，此外还有故障遍历算法［2］、最小路法［3］、最小割集法［4］和分块算法［5］等。但上述算法均基于元件可靠性参数为确定值的假设。实际上，原始参数的数值及其概率分布可能会因为统计资料不足或统计误差以及对电网未来运行条件和环境预测不足而具有不确定性［6］。为使评估结果能更准确地反映系统实际运行的情况，应充分考虑参数不确定性的影响［7］。近年来，区间分析方法将可靠性参数作为区间数处理，可通过一次运算评估负荷点和系统的区间可靠性指标，且从全局角度实现可靠性评估［8］。

贝叶斯网络［9］是20世纪80年代后期新兴起的一种人工智能方法，基于其推理模式能辨识系统薄弱环节，并提出有针对性的改进措施［10］。贝叶斯网络已应用于配电网可靠性评估，提高了配电网的经济效益。文献［11］基于故障树分析法建立贝叶斯网络，实现配电网的可靠性评估。文献［12］以配电网各元件、分块、负荷点及系统状态为节点，以它们之间的影响关系为有向边，建立配电网可靠性评估的4层贝叶斯网络，实现配电网的可靠性计算和薄弱环节辨识。但上述算法均未计及元件可靠性参数的不确定性，且未计及开关设备的故障。

基于贝叶斯网络的双向推理模式，且计及参数的不确定性，本文提出计及开关故障的配电网可靠性评估的贝叶斯网络区间算法，能更加高效地进行参数为区间数的配电网可靠性计算和薄弱环节辨识。

1 区间数的基本运算

本文主要研究非退化正区间数［13］，利用其进行配电网可靠性评估时，可能涉及其四则运算和排序相关知识。其加法、减法和乘法运算均采用文献［14］的定义，排序则采用文献［15］定义的矩阵排序法。

配电网可靠性评估中，可靠性指标计算的区间算法涉及正区间数的除法。由于区间除法运算存在“相关性问题”［16］，其不再是区间乘法的逆运算，且会引起运算结果超宽度。为解决上述问题，须对参与除法运算的区间数标准化［13］，并用重新定义的区间除法进行计算［17］。

设［x］ = ［xmin，xmax］、［y］= ［ymin，ymax］均为非退化正区间数，将其化为标准式为:

其中

令［x1］=［μ1，1］，［x2］=［μ2，1］，文献［15］称之为基本区间数，并定义新的除法公式(用■表示)为:

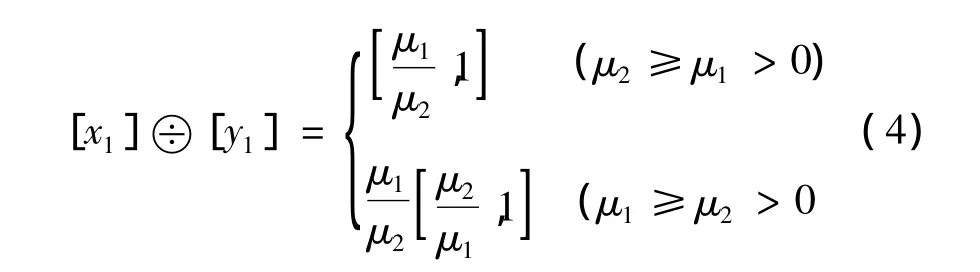
利用文［15］的方法进行区间数除法运算可以得到正确合理的结果，但步骤较繁。实际上，联立式(1)～(4)，可得非退化正区间数除法的较为简单的公式:

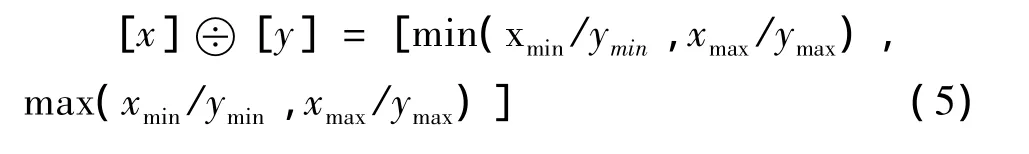
2 配电网可靠性评估贝叶斯网络区间算法

贝叶斯网络是随机事件间概率关系的图形表示［12］，基于其前向推理模式，可计算出负荷点和系统的区间可靠性指标;基于其后向推理模式，可通过元件的可靠性参数和负荷点的节点类型辨识负荷点的薄弱环节，并可通过各元件分摊的区间ENS辨识系统的薄弱环节。

图1为一个简单中压配电网示意图。为简化起见，本文以该配电网为例，建立其可靠性评估的贝叶斯网络，并在此基础上建立其可靠性计算及薄弱环节辨识的区间模型。

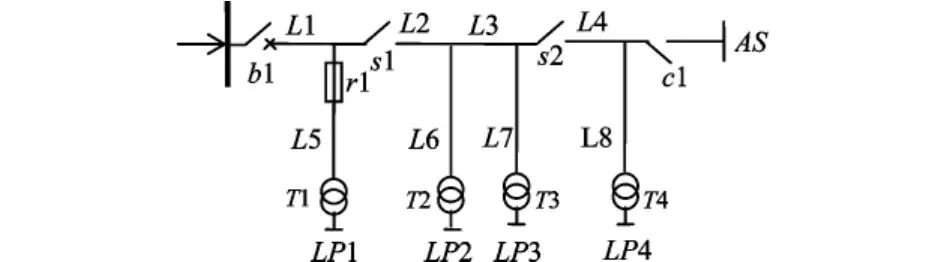
图1 简单配电网示意图

2.1 贝叶斯网络的建立

基于文献［12］所述流程，建立图1配电网可靠性评估的四层贝叶斯网络，如图2所示:

2.2 基于贝叶斯网络的可靠性计算及薄弱环节分析

若用“1”表示元件或分块的故障状态及负荷点的停运状态、“0”表示正常状态，则图2中的贝叶斯网络是一个典型的“或”节点模型。这是由于分块中任意一个元件故障，均可造成其所在分块的元件停运;同样地，对某负荷点的供电有影响的任一分块或开关元件故障，均可造成该负荷点停运。

2.2.1 分块的区间可靠性参数计算

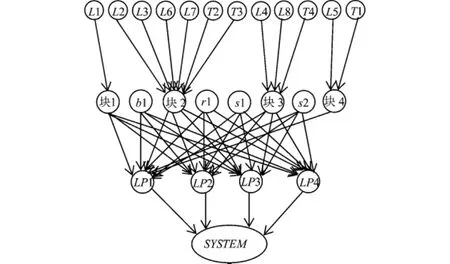
图2 图1配电网可靠性评估的贝叶斯网络

基于以上分析，利用贝叶斯网络的前向推理功能，并引入第1节所述的区间数四则运算法则，采用多元件串联公式计算分块的等效区间可靠性参数，如下:

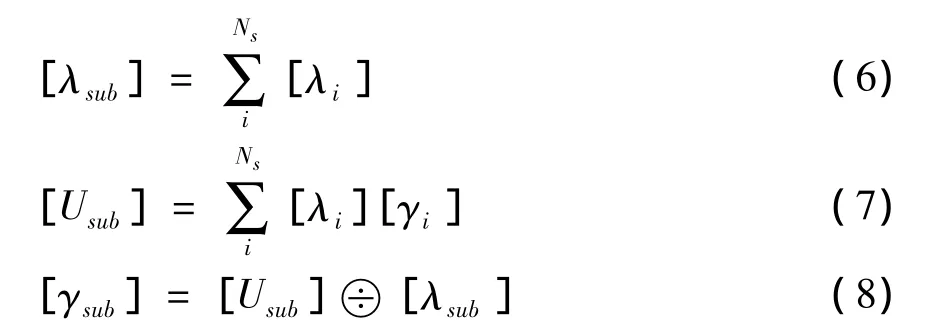
式中，sub为待分析的分块;［λi］、［γi］分别为元件 i的区间故障率、区间修复时间;［λsub］、［γsub］分别为分块的区间等值故障率、区间等值修复时间;Ns为分块包含的元件数。

分块的区间等值修复时间的计算涉及区间除法运算，为避免相关性问题导致运算结果超宽度［16］，本文利用第1节的分析求解式(8)。

2.2.2 负荷点的区间可靠性指标计算及薄弱环节分析

同上述分析类似，得负荷点的区间可靠性指标为:

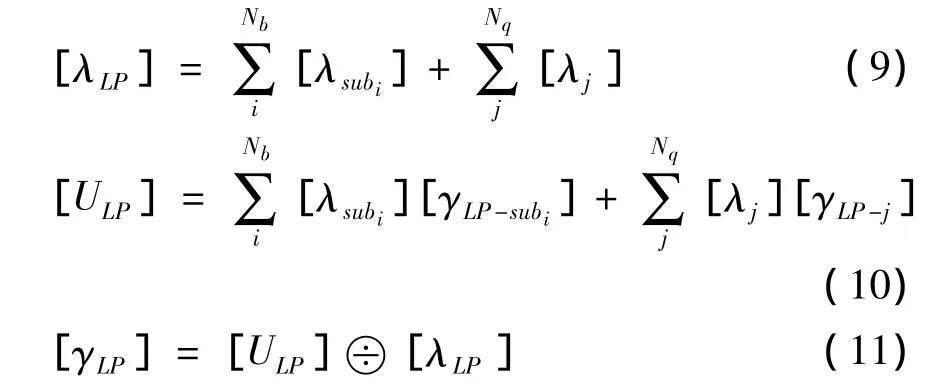
式中，LP 为待分析的负荷点;［λsubi］、［λj］分别为对负荷点的供电有影响的块i和开关j的区间等值故障率;［γLP-subi］、［γLP-j］分别为块 i和开关 j故障时负荷点的区间缺电时间，其取值决定于其故障时负荷点的节点类型;［λLP］、［γLP］分别为负荷点的区间故障率和区间修复时间;Nb为对负荷点有影响的分块数目;Nq为对负荷点有影响的开关数目。

利用贝叶斯网络的后向推理模式辨识负荷点的薄弱环节，即:若观测到系统中某负荷点缺电，反过

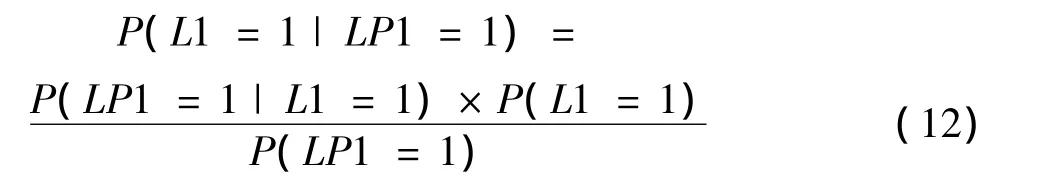
根据图2贝叶斯网络结构，知线路L1属于块1，而块1故障会引起负荷点 LP1停运，因此上式中的P(LP1=1|L1=1)=1。式(12)可写为:来分析系统中哪个元件对该事件影响最大。

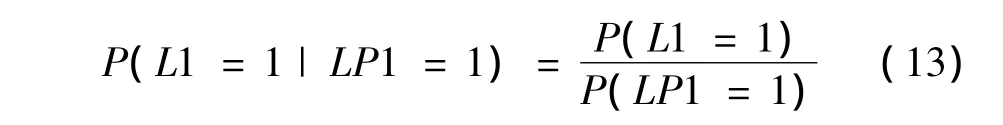
以负荷点LP1为例进行说明。已知负荷点LP1停运，其由线路L1故障引起的后验概率［12］为:

当元件可靠性参数为区间数时，根据第1节的分析，得区间后验概率为:

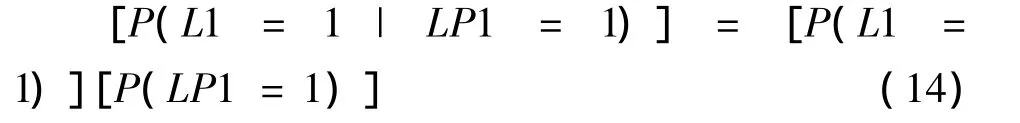
其中，

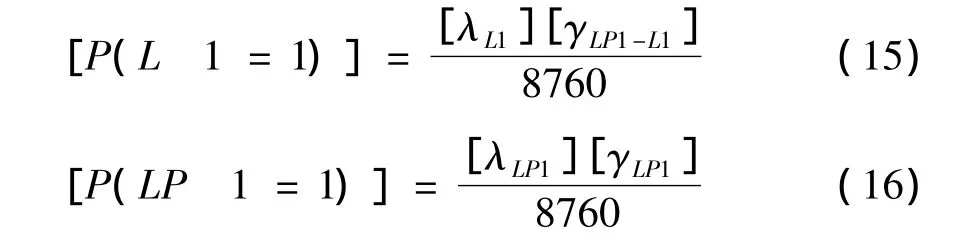
分别为L1故障对LP1停运的区间贡献概率和LP1的区间停运概率，［γLP1-L1］为L1故障引起LP1的区间停运时间。

对其他对LP1供电有影响的元件，都能得出类似(14)～(16)的式子。

由上可知:区间后验概率取决于元件的区间可靠性参数及负荷点的节点类型。计算每个元件故障引起某一负荷点停运的区间后验概率，并按文献［15］所述方法排序，其中最大者对应的元件故障最可能造成该负荷点停运，其为该负荷点的薄弱环节。

2.2.3 系统的区间可靠性指标计算及薄弱环节分析

在计算负荷点的区间可靠性指标的基础上，可进一步计算系统的区间可靠性指标。常见系统指标计算公式的区间形式如下:

①系统平均停电频率指标SAIFI(System average interruption frequency index)

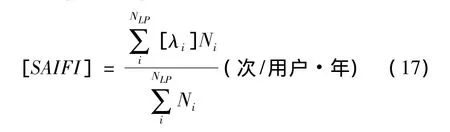
其中［λi］和Ni分别为负荷点i的用户区间停运率和用户数，NLP为系统负荷点总数。

②系统平均停电持续时间SAIDI(System average interruption duration index)

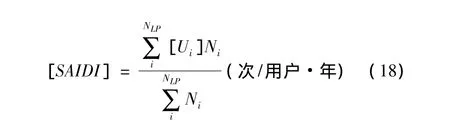
其中［Ui］= ［λi］［γi］，为负荷点i的区间年平均停运时间，小时/年。

③用户平均停电持续时间CAIDI(Customer average interruption duration index)

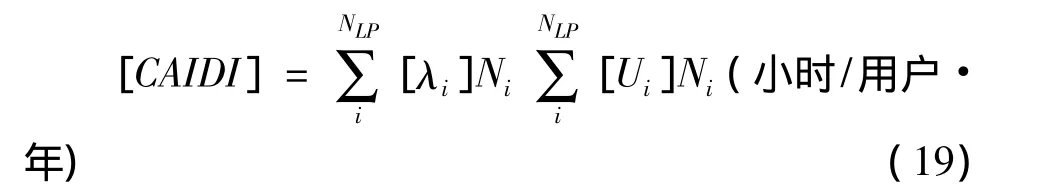
④平均供电可用率指标ASAI(Average service availability index)

⑤系统缺供电量指标ENS(Energy not supplied)

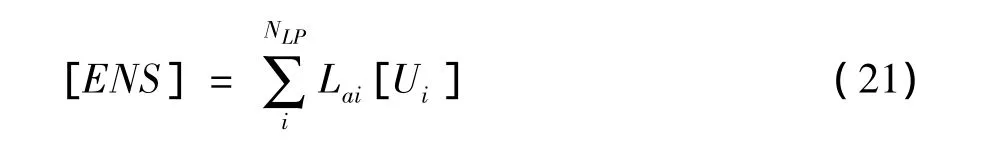
Lai为负荷点i的平均负荷(kW)。

由前述分析知:后向推理只能辨识负荷点的薄弱环节，而不能从全局的角度辨识整个配电网的薄弱环节。故选择配电网的ENS指标进行分析，根据各元件分摊的区间ENS确定配电网的薄弱环节。

配电网中第j个元件分摊的区间ENS为:

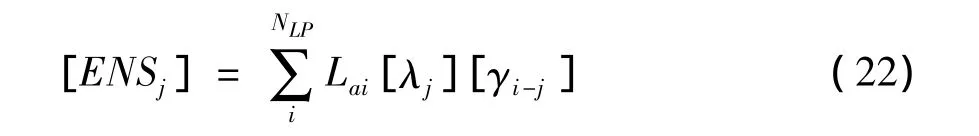
式中，Lai为第i个负荷点的负荷，［λj］为第 j个元件的区间故障率，［γi-j］为仅第j个元件故障时第i个负荷点的区间缺电时间。

以线路L3为例进行分析。根据图2贝叶斯网络结构，确定L3属于块2，其故障时负荷点LP2和LP3的缺电时间均为L3的修复时间，LP1的缺电时间为块2的前向分段开关s1的操作时间，LP4的缺电时间为切换开关c1的操作时间。L3分摊的区间ENS为:

根据式(23)计算每个元件分摊的区间ENS，并按文［15］所述方法排序，分摊量最大者为系统中最薄弱的元件。

3 算例分析

利用以上算法对RBTS系统母线2的馈线F3进行区间可靠性计算及薄弱环节分析。

假设各线路、变压器的故障率和修复时间、分段开关和切换开关的操作时间在文献［18］原始参数的±10%范围内变化，断路器、分段开关和熔断器的故障率为［0.004，0.008］次/年，修复时间为［3，5］小时/次。按文［18］的第5种接线方式进行计算，即主馈线上配置分段开关、分支线保护、备用电源和备用变压器。系统的接线图如图3所示。

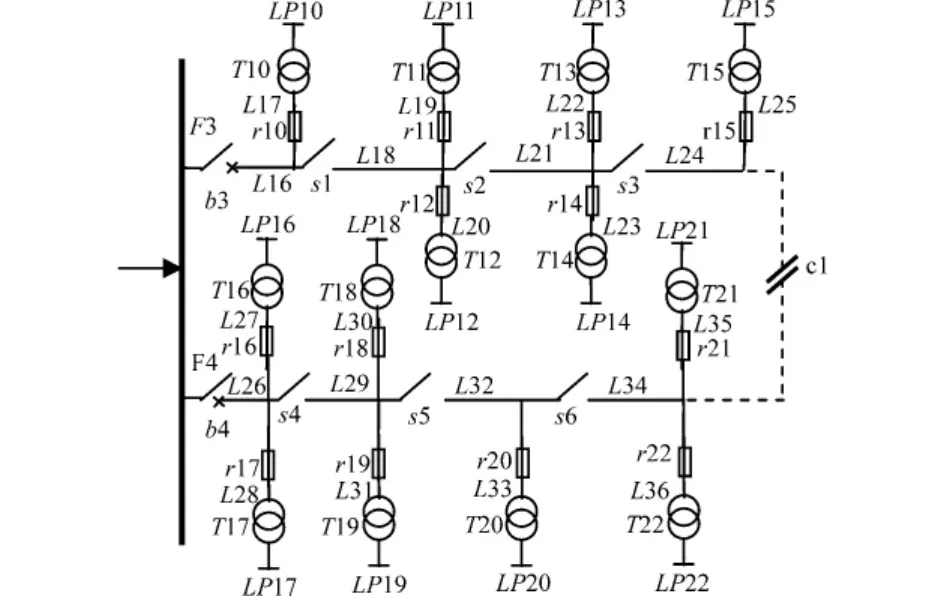
图3 RBTS母线2的系统接线图

3.1 负荷点区间可靠性计算及薄弱环节分析

利用式(6)～(8)，对计及开关故障的情形计算各负荷点的区间可靠性指标，结果如表1所示:

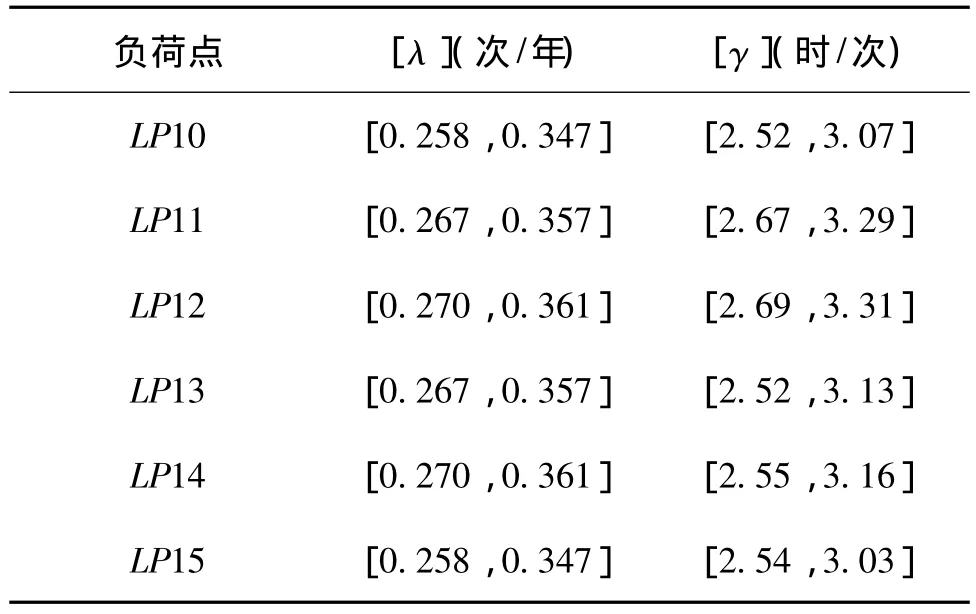
表1 RBTS-BUS2馈线3负荷点的区间可靠性指标

从以上结果可知:区间算法考虑了元件可靠性参数的可能波动范围，可同时给出最好和最差两种情况下的负荷点可靠性指标。

应用2.2.2节负荷点的薄弱环节辨识技术，分析该配电网的负荷点薄弱环节。

以负荷点LP10为例，利用式(14)计算各元件故障引起其停运的区间后验概率，列于表2。

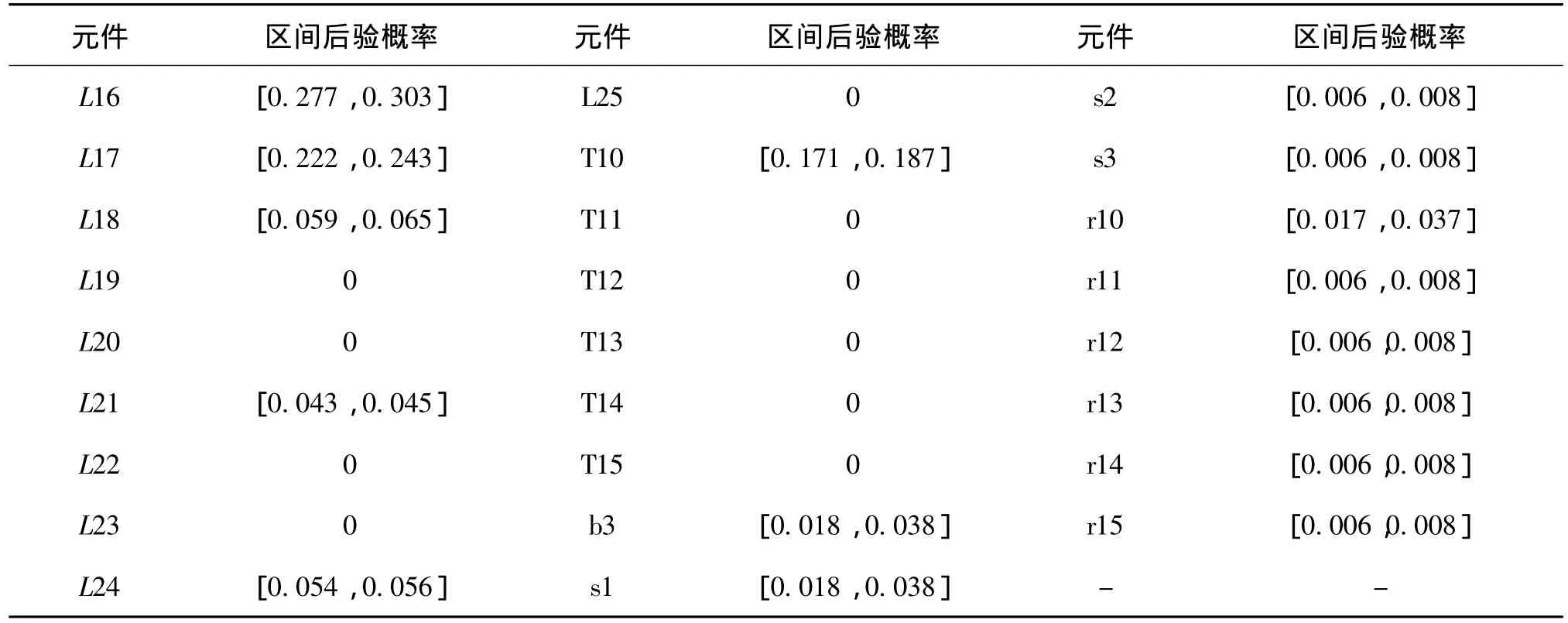
表2 RBTS-BUS2馈线3各元件故障引起负荷点10停运的区间后验概率

利用文献［15］所述的区间数矩阵排序法对上述计算结果进行排序，可知:元件L16对应的区间后验概率最大，其为负荷点LP10的薄弱环节。

利用上述方法可辨识该配电网所有负荷点的薄弱环节，列于表3。

在实际配电网中，可利用上述方法识别重要负荷点的薄弱环节，采取相应改善措施以提高其可靠性。

3.2 系统区间可靠性计算及薄弱环节分析

对计及开关故障的情形进行系统区间可靠性计算，其结果如表4所示。

表3 RBTS-BUS2馈线3各负荷点的薄弱环节

表4 计及开关故障的RBTS-BUS2馈线3的区间可靠性

从表4可知:区间算法考虑了元件可靠性参数的可能波动范围，可同时给出最好和最差两种情况下的系统可靠性指标。

根据2.2.3节分析，将计及开关故障时每个元件分摊的区间ENS列于表5。

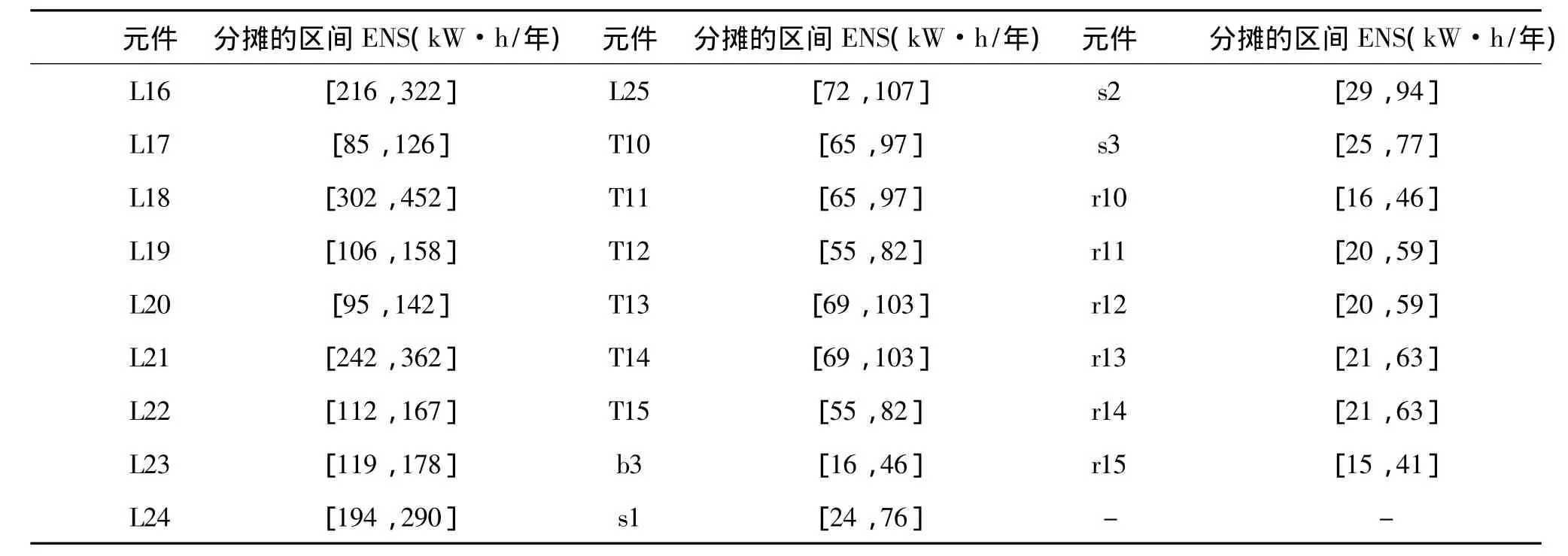
表5 RBTS-BUS2馈线3各元件分摊的区间ENS

利用文献［15］所述的区间数矩阵排序法对上述计算结果进行排序，可知:干线L16、L18、L21分摊的ENS较多。其中，L18分摊的ENS最多，其为配电网的最薄弱环节。

表5的计算结果表明，L16是比L25更加薄弱的环节。为验证上述算法的正确性，将L16和L25的故障率分别置0并计算系统的区间可靠性指标，结果如表6所示。

表6 RBTS-BUS2馈线3将L16和L25的故障率分别置0时的区间可靠性指标

将表6与表4的结果对比可知:改善L16的可靠性比改善L25的可靠性对提高整个配电网的可靠性水平效果更为显著，验证了2.2.3节薄弱环节分析方法的正确性和有效性。

在实际配电网中，可利用上述方法识别系统的薄弱环节，并采取相应改善措施以提高其可靠性。

4 结论

本文提出一种配电网可靠性评估贝叶斯网络区间算法。该算法以各元件、分块、负荷点及系统的状态为随机变量，分析它们之间的关联关系和影响关系，建立配电网可靠性评估的4层贝叶斯网络。

为充分计及元件可靠性参数的不确定性，引入区间数运算法则，基于贝叶斯网络的前向推理模式计算负荷点和系统的区间可靠性指标。

基于贝叶斯网络的后向推理模式，提出通过元件的区间可靠性参数和负荷点节点类型辨识负荷点的薄弱环节的方法，及通过各元件分摊的区间ENS辨识系统的薄弱环节的方法。对实际配电网，可根据前述方法辨识配电网薄弱环节，并采取相应改善措施以提高系统可靠性。

通过对IEEE RBTS母线2等算例的分析，验证了本文贝叶斯网络可靠性评估区间算法及薄弱环节辨识技术的正确性和有效性。

［1］ 陈文高.配电系统可靠性实用基础［M］.北京:中国电力出版社，1998:117-124.

［2］ 李志民，李卫星，刘迎春.辐射状配电系统可靠性评估的故障遍历算法［J］.电力系统自动化，2002，(2):53-56.

［3］ 戴雯霞，吴捷.基于最小路的配电网可靠性快速评估法［J］.电力自动化设备，2002，(7):29-31.

［4］ 杨文宇，余健明.基于最小割集的配电系统可靠性评估算法［J］. 西安理工大学学报，2001，(4):387-391.

［5］ 谢开贵，王小波.计及开关故障的复杂配电系统可靠性评估［J］. 电网技术，2008，(19):16-21.

［6］ 任震，万官泉，黄雯莹.参数不确定的配电系统可靠性区间评估［J］.中国电机工程学报，2003，(12):68-73.

［7］ 郑彦芹，娄北，张鸿雁，等.基于区间数和价值理论的配电网可靠性评估［J］.电力系统保护与控制，2008，(18):19-23.

［8］ 张鹏，王守相.大规模配电系统可靠性评估的区间算法［J］.中国电机工程学报，2004，(3):77-84.

［9］ 霍利民，朱永利，张立国，等.用于电力系统可靠性评估的贝叶斯网络时序模拟推理算法［J］.电工技术学报，2008，(6):89-95.

［10］ Yu D C，Nguyen T C，Haddawy P.Bayesian Network Model for Reliability Assessment of Power Systems［J］.IEEE Trans on Power Systems，1999，(2):426-432.

［11］ 卢锦玲，杨晓东，粟然，等.一种基于贝叶斯网络的配电网可靠性评估方法［J］.华北电力大学学报，2004，(2):16-19.

［12］ 刘禹良，谢开贵，曹侃.基于贝叶斯网络和分块技术的配电网可靠性评估［J］.华东电力，2010，(5):90-95.

［13］ 王清印，吕瑞华.区间数的标准表示及其四则运算法则与泛灰数的内在联系［J］.数学的实践与认识，2005，(6):216-222.

［14］ Alefeld G，Mayer.Interval Analysis:Theory and Applications［J］.Journal of Computational and Applied Mathematics，2000，(1-2):421-464.

［15］ 李志林.区间数的一种改进的排序方法［J］.数学的实践与认识，2004，(6):124-127.

［16］ 张鹏.区间分析在电力系统可靠性评估中的应用研究［D］.北京:清华大学，2002.

［17］ 周志仁，周俊建，张志海.区间数逆运算和简单的区间数方程［J］.河北煤炭建筑工程学院学报，1994，(2):47-51.

［18］ R.N.Allan，R.Billinton，I.Sjarief，et al.A Reliability Test System for Educational Purposes:Basic Distribution System Data and Result［J］.IEEE Trans on Power Systems，1991，(2):813-820.